神经网络的激活函数是一种非线性函数,它被应用于每个神经元的输出,以引入非线性性质到网络中。
激活函数的目的是将输入转换为输出,并且将输出限制在特定的范围内。它们非常重要,因为线性变换(例如加法和乘法)的组合只会产生与输入相同的线性关系。通过使用非线性的激活函数,神经网络能够学习和表示更复杂的函数关系。
常用的激活函数包括:
1. Sigmoid函数:它将输入映射到0到1之间的连续输出。它在二分类问题中常用作输出层的激活函数,在隐藏层中使用会导致梯度消失的问题。
2. tanh函数:也被称为双曲正切函数,将输入映射到-1到1之间的连续输出。与Sigmoid函数相比,它的输出范围更大,但依然存在梯度消失的问题。
3. ReLU函数:也被称为修正线性单元函数,它将负输入映射为0,并保持正输入不变。它在隐藏层中非常常用,因为它能够处理梯度消失问题,并加速网络的训练速度。
4. Leaky ReLU函数:是ReLU函数的一种改进形式,解决了ReLU函数在负数部分出现的“死神经元”问题。它在负输入时引入一个小的负斜率,以便保持负数部分的信息流动。
5. Softmax函数:通常用于多分类问题的输出层。它将输入向量归一化为概率分布,使得所有输出值的总和为1。
这些是神经网络中常见的激活函数,选择合适的激活函数取决于问题的特点和网络的架构。
以下是使用Python绘制这几种函数的曲线的示例代码:
import numpy as np
import matplotlib.pyplot as plt
# Sigmoid函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# tanh函数
def tanh(x):
return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
# ReLU函数
def relu(x):
return np.maximum(0, x)
# Leaky ReLU函数
def leaky_relu(x, alpha=0.01):
return np.maximum(alpha * x, x)
# Softmax函数
def softmax(x):
exps = np.exp(x)
return exps / np.sum(exps)
x = np.linspace(-10, 10, 100)
# 绘制Sigmoid函数曲线
plt.plot(x, sigmoid(x), label='Sigmoid')
# 绘制tanh函数曲线
plt.plot(x, tanh(x), label='tanh')
# 绘制ReLU函数曲线
plt.plot(x, relu(x), label='ReLU')
# 绘制Leaky ReLU函数曲线
plt.plot(x, leaky_relu(x), label='Leaky ReLU')
# 绘制Softmax函数曲线
plt.plot(x, softmax(x), label='Softmax')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
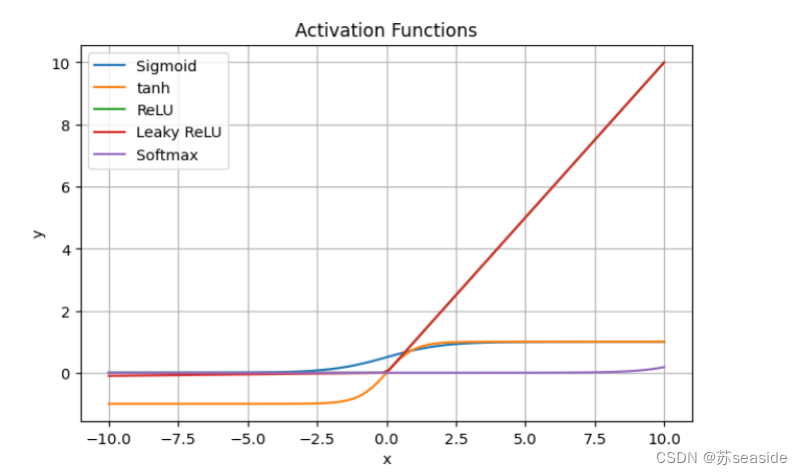
plt.title('Activation Functions')
plt.grid()
plt.show()
-
Sigmoid函数的曲线特点是在输入接近正无穷大和负无穷小的时候,输出接近于1和0。它的输出范围是0到1之间,且曲线在中心点处斜率最大。
-
tanh函数的曲线特点是在输入接近正无穷大和负无穷小的时候,输出接近于1和-1。与Sigmoid函数相比,它的输出范围更大,且曲线在中心点处斜率最大。
-
ReLU函数的曲线特点是在输入小于零时输出为0,大于零时输出等于输入。它的图像为一条直线段,没有平滑的转折点,且在中心点处斜率始终为1。
-
Leaky ReLU函数的曲线特点与ReLU函数类似,但在负输入时引入了一个小的负斜率。这个负斜率可以防止负数部分的输出完全消失,增加了模型的稳定性。
-
Softmax函数的曲线特点是将输入向量归一化为概率分布。它的输出是一个概率分布,且所有输出值的总和为1。该函数适用于多分类问题,并且在输出层使用时可以将每个类别的输出解释为概率。