【损失函数】Quantile Loss 分位数损失

news2024/11/16 4:23:15

1、介绍

Quantile Loss（分位数损失）是用于回归问题的一种损失函数，它允许我们对不同分位数的预测误差赋予不同的权重。这对于处理不同置信水平的预测非常有用，例如在风险管理等领域。

当我们需要对区间预测而不单是点预测时 分位数损失函数可以发挥很大作用

2、公式

$J_{\text {quant }}=\frac{1}{N} \sum_{i=1}^N \mathbb{I}_{\hat{y}_i \geq y_i}(1-\gamma)\left|y_i-\hat{y}_i\right|+\mathbb{I}_{\hat{y}_i<y_i} \gamma\left|y_i-\hat{y}_i\right|$

其中， ${y}_i$ 是实际目标值， $\hat{y}_i$ 是模型的预测值， $\gamma$ 是分位数水平，通常取值在 0 和 1 之间。

我们如何理解这个损失函数呢？这个损失函数是一个分段的函数，将 $\hat{y}_i \geq y_i$ （高估）和 $\hat{y}_i<y_i$ （低估）两种情况分开来，并分别给予不同的系数。当 $\gamma > 0.5$ 时，低估的损失要比高估的损失更大，反过来当 $\gamma < 0.5$ 时，高估的损失比低估的损失大；分位数损失实现了分别用不同的系数控制高估和低估的损失，进而实现分位数回归。特别地，当 $\gamma = 0.5$ 时，分位数损失退化为 MAE 损失，从这里可以看出 MAE 损失实际上是分位数损失的一个特例 — 中位数回归（这也可以解释为什么 MAE 损失对 outlier 更鲁棒：MSE 回归期望值，MAE 回归中位数，通常 outlier 对中位数的影响比对期望值的影响小）。

简单的总结下，分位数损失通过 $\gamma$ 的不同取值来避免过拟合和欠拟合，实现分位数回归。

分位数值的选择基于在实际中需要误差如何发挥作用，即在过程中误差为正时发挥更多作用还是在误差为负时发挥更大作用。

3、图像

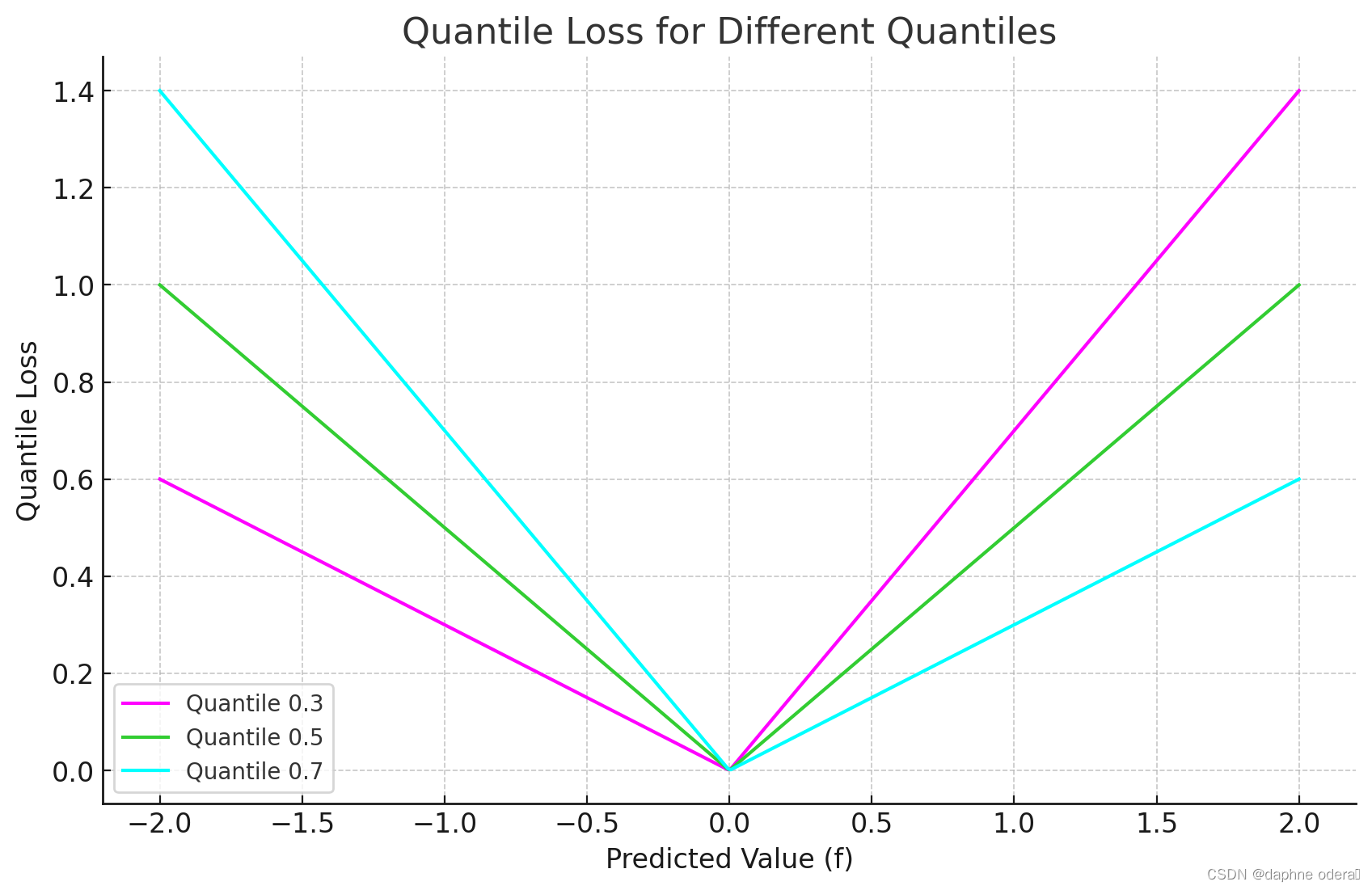
上图是分位数损失（Quantile Loss）在分位数为 0.3、0.5、0.7 时的图像。图中显示了预测值（f）与分位数损失之间的关系，可以看到 0.3 和 0.8 在高估和低估两种情况下损失是不同的，而 0.5 实际上就是 MAE。

4、实例

假设我们有以下情况：我们正在训练一个模型来预测房价涨幅区间。我们有以下目标值（真实值）和预测值：

目标（真实值）: [2.0, 1.0, 4.0, 3.5, 5.0]
预测: [1.8, 0.9, 3.5, 3.0, 4.8]

我们使用 Quantile Loss作为损失函数：

import torch
import torch.nn as nn

class QuantileLoss(nn.Module):
    def __init__(self, quantile):
        super(QuantileLoss, self).__init__()
        self.quantile = quantile
    def forward(self, y, y_pred):
        residual = y_pred - y
        loss = torch.max((self.quantile - 1) * residual, self.quantile * residual)
        return torch.mean(loss)
# 示例数据
y_true = torch.tensor([2.0, 1.0, 4.0, 3.5, 5.0], dtype=torch.float32)
y_pred = torch.tensor([1.8, 0.9, 3.5, 3.0, 4.8], dtype=torch.float32)
# 定义分位数水平 当分位数为 0.5 时，分位数损失退化为 MAE 损失
quantile = 0.5
# 初始化损失函数
quantile_loss = QuantileLoss(quantile)
# 计算损失
loss = quantile_loss(y_true, y_pred)
# Quantile Loss: 0.14999999105930328
print(f'Quantile Loss: {loss.item()}')

在上述示例中，我们使用了一个简单的自定义 PyTorch 模块 `QuantileLoss`，它采用分位数水平作为参数，并计算相应的 Quantile Loss。这个例子中使用的分位数是 0.5，即中位数。此时分位数损失退化为 MAE 损失，实际应用中根据不同需求设定不同的分位数水平。