【双指针算法】-- 左右指针

news2025/11/4 9:19:36

左右指针

前言
一、双指针算法
二、左右指针
- 1.用于在已排序数组中找到两个数使其和为特定值
- 2.在字符串中判断是否为回文
总结

前言

今天在刷Leetcode的时候觉得自己双指针掌握的还是不错的记录一下,写个学习笔记,也方便以后翻阅,如果也帮助到你了,那真是太好啦! 本篇介绍的是左右指针。

一、双指针算法

双指针算法（Two Pointers Algorithm）是一种常用于数组或链表等数据结构的算法思想。它通常涉及到使用两个指针，它们可能位于数组的不同位置，以便在数组中进行某种操作或搜索。双指针算法的目标是通过调整指针的位置来解决问题。在实际应用中，双指针算法常常能够在O(n)的时间复杂度内解决问题。

快慢指针
左右指针
滑动窗口
对撞指针

二、左右指针

用于在已排序数组中找到两个数使其和为特定值。
在字符串中判断是否为回文。

左右指针分别从数组或字符串的两端出发，根据问题的要求，通过移动指针的位置来解决问题。
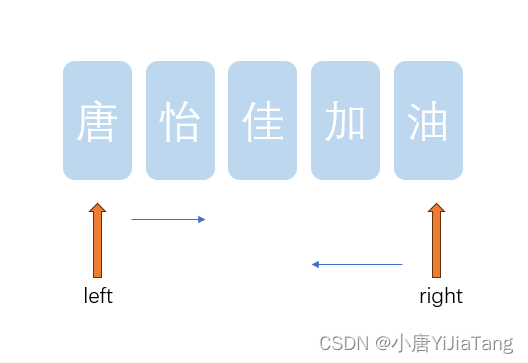
在这里插入图片描述

1.用于在已排序数组中找到两个数使其和为特定值

#include <vector>

std::vector<int> twoSum(std::vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;
    //始终保持左指针在右指针左边
    while (left < right) {
        int currentSum = nums[left] + nums[right];
        //两数之和大于目标值,右指针左移
        if (currentSum > target) {
            right--;
        //两数之和小于目标值,左指针右移
        } else if (currentSum < target) {
            left++;
        } else { //两数之和等于目标值
            return {nums[left], nums[right]};
        }
    }
    return {}; // 如果找不到符合条件的数对
}

在leetcode中如题15–三数之和
在这里插入图片描述
因为是双指针加一层循环,时间复杂度为O(N^2)

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        int nums_size = nums.size();
        vector<vector<int>> ans;
        if (nums_size < 3) return ans;
        std::sort(nums.begin(), nums.end());
        for (int i = 0; i < nums_size; i++) {
            if (nums[i] > 0) return ans;
            if (i > 0 && nums[i] == nums[i - 1]) continue;//去重
            int left = i + 1;
            int right = nums_size - 1;
            while (left < right) {
                if (nums[i] + nums[left] + nums[right] < 0) {
                    left++;
                }
                else if (nums[i] + nums[left] + nums[right] > 0) {
                    right--;
                }
                else {
                    ans.push_back(vector<int>{nums[i], nums[left], nums[right]});
                    left++;
                    right--;
                    while (left < right && nums[left] == nums[left - 1]) left++;//去重
                    while (left < right && nums[right] == nums[right + 1]) right--;//去重
                } 
            }
        }
        return ans;
    }
};

题18–四数之和
在这里插入图片描述

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        int nums_size = nums.size();
        std::sort(nums.begin(), nums.end());   //排序
        vector<vector<int>> ans;
        if (nums_size < 4) return ans;         //排除特殊情况
        for (int i = 0; i < nums_size; i++) {  //遍历
            if (i > 0 && nums[i] == nums[i - 1]) continue;//去重
            for (int j = i+1; j < nums_size; j++) {   //三数之和
                if (j > i + 1 && nums[j] == nums[j - 1]) continue;//去重
                int left = j + 1;
                int right = nums_size - 1;
                while (left < right) {
                    if (long (long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right])) < target) {
                        left++;
                    }else if (long (long(nums[i]) + long(nums[j]) + long(nums[left]) + long(nums[right])) > target) {
                        right--;
                    }else {
                        ans.push_back(vector<int>{nums[i], nums[j],nums[left],nums[right]});
                        left++;
                        right--;
                        while (left < right && nums[left] == nums[left - 1]) left++;  //去重
                        while (left < right && nums[right] == nums[right + 1]) right--; //去重
                    }
                }
            }
        }
        return ans;
    }
};

这里的四数之和其实就是遍历了一遍三数之和,所以时间复杂度为O(N^3),注意这两题在做右指针的基础上,还需要考虑去重和排序。

2.在字符串中判断是否为回文

回文是指一个字符串从左到右读和从右到左读是一样的,如’‘tyjjyt’’

#include <string>

bool isPalindrome(const std::string& s) {
    int left = 0;
    int right = s.size() - 1;
    //始终保持左指针在右指针左边
    while (left < right) {
        if (s[left] != s[right]) {
            return false;
        }
        left++;
        right--;
    }
    return true;
}