后缀表达式计算

过程分析

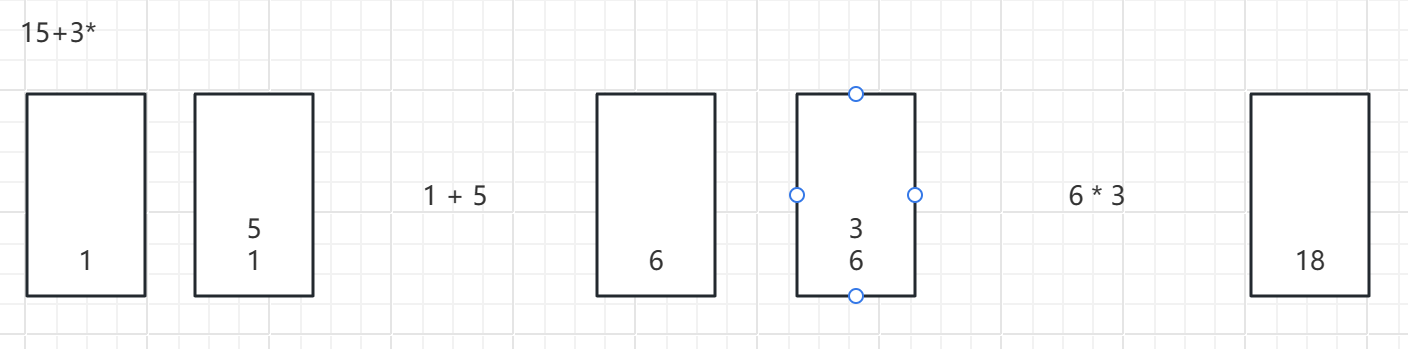
• 中缀表达式 （1+5）*3 => 后缀表达式 15+3* (可参考这篇文章：中缀转后缀)
  • 第一步：我们从左至右扫描 后缀表达式(已经存放在一个字符数组中)，遇到第一个数字字符 ‘1’ 放入栈中
  • 第二步：接着扫描，遇到数字字符 ‘5’,放入栈中
  • 第三步：接着扫描，遇到 运算字符 ‘+’，连着两次出栈b a，计算 a 运算符 b 的值，将其结果值放入栈中（b：5，a：1）
  • 第四步：接着扫描，遇到数字字符 ‘3’ 放入栈中
  • 第五步：接着扫描，遇到运算字符 ‘*’ 连着两次出栈b a，计算 a 运算符 b 的值，将其结果只放入栈中（b：3，a：6）
  • 第六步：扫描结束，返回栈顶元素

图解

代码分析

• 思路：表达式存储在一个字符数组 exp[] 中，遇到数值得时候 入栈，遇到运算符的时候 出栈（连续两次）然后拿两个数值 a 和 b 以及运算符 Op 进行计算，最后将计算结果再入栈，直到遍历到字符数组结尾为止！

  // 运算函数，用来计算 a Op b （Op 是运算符）
  int op(int a , int b , char Op){
      if(Op == '+')
          return a + b;
      if(Op == '-')
          return a - b;
      if(Op == '*')
          return a * b;
      if(Op == '/'){
          if(b == 0){					// 分母不能为零
              cout<<"ERROR"<<endl;
          }else{
              return a/b;
          }
      }
  }
  
  // 计算后缀表达式
  int com(char exp[]){
      int i , a , b , c;
      // 创建顺序栈
      int stack[maxSize];
      // 初始化栈顶指针
      int top = -1;
      // 存储运算符
      char Op;
      for(i = 0;exp[i] != '\0'; ++i){
          if(exp[i] >= '0' && exp[i] <= '9'){			// 是数字
              stack[++top] = exp[i] - '0';			// 将数字字符变成数字
          }else{
              Op = exp[i];
              // 连续两次出栈
              b = stack[top--];
              a = stack[top--];
              
              c = op(a , b , Op);						// 计算结果
              stack[++top] = c;						// 计算结果入栈
          }
      }
      return stack[top];
  }