46. Permutations
Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.
Example 1:
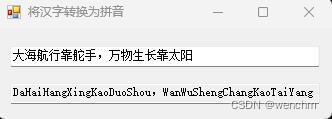
Input: nums = [1,2,3] Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 思路:此题可用回溯法做排列问题。待取元素的candiate内无重复,区别于之前的组合问题,这里在横向遍历时for循环需要遍历所有元素,而不是在startIndex之后的元素(因为排列可以取[1,2,3],[1,3,2]这样的元素,组合的话就只能取[1,2,3],而无[1,3,2])。但是为了避免与纵向已经取过的元素在一个path里重复,要设置一个used元素记录之前path里已经取过的元素。这个used元素也需要在回溯中调整。
class Solution(object):
def backtrack(self, nums, path, result, used):
if len(path) == len(nums):
result.append(path[:]) # 记得用[:]
return
for i in range(len(nums)): # use used to remove duplicated item
if used[i]:
continue
used[i] = True
path.append(nums[i])
self.backtrack(nums, path, result, used)
path.pop()
used[i] = False
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
result = []
used = len(nums) * [False]
self.backtrack(nums, [], result, used)
return result
491. Non-decreasing Subsequences
Given an integer array nums, return all the different possible non-decreasing subsequences of the given array with at least two elements. You may return the answer in any order.
Example 1:
Input: nums = [4,6,7,7] Output: [[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
思路:找出一个数组中的所有升序子序列,注意这个子序列不需要在原数组中连续。用递归写出暴力解法的思路枚举出所有可能的子序列就可以了。第i+1层横向遍历从startIndex = i+1开始。
关键点在于去重。其实只要每次横向遍历不用本次横向遍历里已经用过的元素就可以了。因为这个新元素最后可以取得的有效升序子序列之能是之前这个元素可以取得的有效子集。因为有效升序子集不需要连续!!
class Solution(object):
def backtrack(self, nums, startIndex, path, result):
if len(path) > 1:
result.append(path[:])
uset = set()
for i in range(startIndex, len(nums)):
if path and nums[i] < path[-1] or nums[i] in uset: #[2,7,8,4,7,9] 比如这种情况下,第二个7就不能再被取,因为第二个7能组合出来的有效升序子序列一定能被第一个7组合出来。
continue
uset.add(nums[i])
path.append(nums[i])
self.backtrack(nums, i +1, path, result)
path.pop()
def findSubsequences(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
result = []
path = []
self.backtrack(nums, 0, path, result)
return result
47. Permutations II
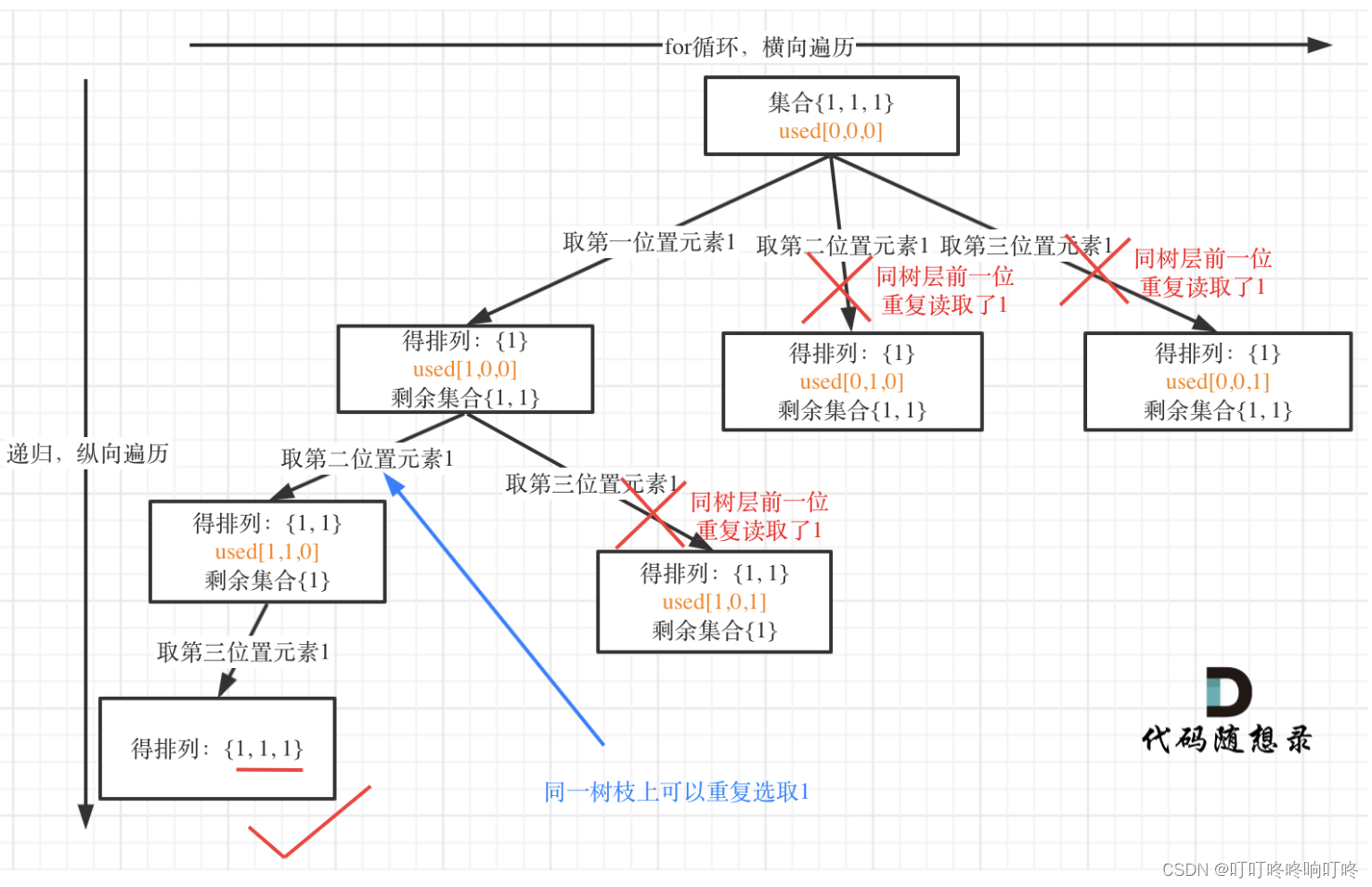
此题乍一看和之前的题很像,应该是一个套路,但是 if (i>0 and nums[i] == nums[i-1] and used[i-1]) or used[i]: 这个两个条件却让我想了很久,这也是此题与之前题目的不同之处。or之后的条件和今天的第一题一致,第一个条件则是结合了排列和元素重复这两个要素得出,可以参见代码随想录里的这个例子。
比如有元素[1,1,1], 第一层取了第一个1,那么第二个和第三个1为避免重复就不可以再取了。进入第二层时,used的情况是[1,0,0]。第二层时,第一个1已经取过了,所以第二层就不可以取第一个1了(对应上述第二中情况),就轮到第二个1了,第二个1之前没有被取过,所以就可以取。第三层时,第一第二个1都不可以取了,就得取第三个1了。
在判断第二层的第二个1是不是要取时,因为第一层时,第一个1已经置true被取过了,且第一层时,第二个1没有被取过,还是false,所以可以取。第二层的第三个1,虽然第一层时第三个元素未被取过还是false,但第二个1也是false,所以为了原数组里重复元素去重,这时候第三个元素不取。
在判断第三层的第二个1是不是要取时,虽然or之前的条件判断可取,但or之后的条件显示因为第二层时,第二个1已经置true被取过了,所以最终不取,但是判断第三层第三个1时,第二层里第二个1被取过了,所以这一层就轮到了第三个1。
以上是我自己目前的理解,不能确定就是完全正确的。如果错漏还请指出。谢谢!
class Solution(object):
def backtrack(self, nums, path, result, used):
if len(nums) == len(path):
result.append(path[:])
return
for i in range(len(nums)):
if (i>0 and nums[i] == nums[i-1] and not used[i-1]) or used[i]:
# 1. 不可以读取的情况也就是当前位和之前位置值相同,且之前位置在之前层已经被读取过了,那么接下来就要轮到当前元素被读取了。
# 2. 或者是当前位置的值在升序序列中虽然是第一次出现,但是该元素在之前的层被用过,排列中也要去掉这个以去重。
# 比如有元素[1,1,1], 第一层取了第一个1,那么第二个和第三个1为避免重复就不可以再取了。进入第二层时,used的情况是[1,0,0]。第二层时,第一个1已经取过了,所以第二层就不可以取第一个1了(对应上述第二中情况),就轮到第二个1了,第二个1之前没有被取过,所以就可以取。第三层时,第一第二个1都不可以取了,就得取第三个1了。
continue
used[i] = True
path.append(nums[i])
self.backtrack(nums, path, result, used)
used[i] = False # 注意!因为回溯,处理每一个元素时,和它同层的元素的情况是未被处理的原始值,看到的处理后的都是上一层的。
path.pop()
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
result = []
nums.sort()
used = [False] * len(nums)
self.backtrack(nums, [], result, used)
return result