深度确定性策略梯度 DDPG

深度确定性策略梯度 DDPG

深度确定性策略梯度 DDPG
模型结构
目标函数
算法步骤
适合场景

深度确定性策略梯度 DDPG

A2C、A3C 都是在线策略，在与环境交互时，样本参数更新效率低，所以主要是应用在离散空间，计算量没那么大。

DDPG 专用于解决连续空间的问题。

设计思路结合了确定性策略（给定状态下，策略会产生一个特定动作，而不是动作的概率分布）和演员-评论家框架。

DDPG 类似 DQN（用神经网络去近似Q函数），再用一个演员-评论家框架去弥补 DQN 不能处理连续控制性问题的缺点。

适用于处理需要精细控制的问题，例如跑车的运动控制，它在连续动作空间中的确表现更好。

模型结构

DDPG 有 4 个神经网络。

两个神经网络（Actor和Critic）
及它们的对应目标网络（Target Actor和Target Critic）

四个网络可用一个舞台剧的比喻来解释：

演员（Actor网络）:
- 就像舞台上的主角，这个演员（Actor网络）需要决定在每个场景中应该做什么动作。比如，他可能需要决定是走向左边还是右边，或者是跳起来还是蹲下。
- 这个网络就像一个深思熟虑的演员，通过学习和实践，慢慢找到在每个场景中的最佳表现方法。
评论家（Critic网络）:
- 然后有一个评论家坐在观众席中，观看演员的每一个动作，并评价这个动作的好坏。这个评论家（Critic网络）会告诉演员他的表演是否能帮助整个剧情的发展。
- 这个网络就像一个专业的剧评人，它帮助演员理解哪些动作对整个剧情最有帮助。
备用演员（Target Actor网络）:
- 还有一个备用演员，他在幕后观察主演员的表演。这个备用演员（Target Actor网络）不会立刻模仿主演员的每一个新动作，而是慢慢地、稳定地学习他的风格。
- 这个网络确保了学习过程不会因为主演员突然的改变而变得混乱。
备用评论家（Target Critic网络）:
- 最后，还有一个备用评论家，他也在评价演出，但更多地是基于过去的表演，而不仅仅是当前的表演。这个备用评论家（Target Critic网络）确保评价标准不会因为短期的变化而频繁变动。
- 这个网络帮助保持评价的一致性和稳定性，确保演员不会因为短期的波动而偏离长期的学习目标。

在DDPG算法中，这四个网络协同工作：演员决定动作，评论家评价这些动作，而备用演员和备用评论家则帮助保持整个学习过程的平稳和连续性。

完整流程图：

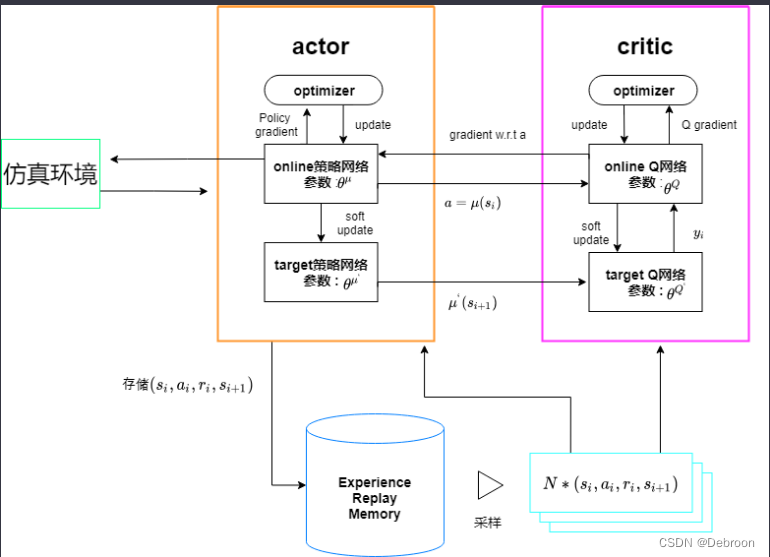
环境交互:
- Agent（Actor和Critic）在环境中执行动作，获得新的状态、奖励和是否结束的信息。这些信息被表示为一个四元组 $s_i, a_i, r_i, s_{i+1})$ 。
经验回放:
- 这些四元组被存储在经验回放内存中。这样做可以帮助算法学习更稳定，因为它减少了样本间的相关性，并且可以重复使用旧的经验来训练。
批样本抽取:
- 从经验回放内存中随机抽取一批四元组来进行学习。这个批量的数据用于更新 Actor 和 Critic 网络。
Critic（评价家）:
- Critic网络使用抽取的样本来评估动作的价值。它有两个组件：
  - Critic网络 $θ^Q)$ : 上图的在线Q网络，使用当前策略和状态来估计Q值（动作的价值）。
  - 目标Critic网络 $θ'^Q)$ : 使用相同的输入，这是Critic网络的复制品，参数更新也比在线Critic网络慢，用于生成一个稳定的目标，以便优化在线Critic网络。
Actor（演员）:
- Actor网络决定给定状态下的最优动作。它也有两个组件：
  - Actor网络 $θ^μ)$ : 上图的在线策略网络，它直接计算当前策略下的动作。
  - 目标Actor网络 $θ'^μ)$ : 这是Actor网络的复制品，其参数更新比在线Actor网络慢。它用于计算目标Q值，以稳定训练过程。
优化器:
- 每个网络（Actor和Critic）都有一个优化器。优化器使用梯度下降方法来调整网络的权重，从而最小化损失函数。
  - Actor优化器：使用策略梯度来更新在线Actor网络的参数，目的是最大化Critic网络预测的Q值。
  - Critic优化器：更新在线Critic网络的参数，目的是最小化预测Q值和目标Q值之间的差异。
软更新:
- 在线网络的权重通过软更新的方式被用来逐渐更新目标网络的权重。这样可以保证目标网络的参数变化不会太大，从而保持训练的稳定性。

整个流程是一个循环过程，Actor和Critic网络的参数通过与环境的交互和优化器的更新不断地进行调整，以此来提升策略的性能。通过这种方式，DDPG算法能够让Agent学会在连续的动作空间内做出决策。

目标函数

价值网络目标函数 = 目标值网络（Target-Q）+ 当前值网络（Current-Q），均分误差最小化俩者之间的差异。

$J_{t}^{\omega}=\text{MSE}(\underbrace{r_{t}+\gamma Q^{w}\left(s_{t+1},\mu_{\theta}\left(s_{t+1}\right)\right)}_{\text{Target-Q}}-\underbrace{Q^{w}\left(s_{t},a_{t}\right)}_{\text{Current-Q}})$

DDPG 使用了目标策略网络：

$J_{t}^{\theta}=-Q^{w}\left(s_{t},\mu_{\theta}\left(s_{t}\right)\right)$

$\underbrace{Q^{w}\left(s_{t+1},\mu_{\theta}\left(s_{t+1}\right)\right)}_{\mu\text{-Target}}$

选 Q 函数负值为目标函数，使策略朝着增加 Q 值的方向进化

策略优化的目标是使 Q 函数的值最大化，即选择能带来最高回报的动作。

使用目标策略网络，减少 Q 函数波动，提升训练稳定性和收敛性

目标策略网络是一种技术，用于稳定学习过程。通过使用稍微落后于最新策略的目标策略，可以减少 Q 函数的波动，从而提高训练过程的稳定性和收敛速度。

算法步骤

DDPG的算法步骤：

初始化网络：在DDPG中，有四个主要的神经网络 - Actor网络和Critic网络及它们各自的目标网络（Target Actor和Target Critic）。Actor网络负责确定给定状态下的动作，而Critic网络则评估这个动作的好坏（即动作的价值）。
收集经验：算法通过与环境交互来收集经验。在每一步，根据当前状态和Actor网络来选择动作，然后执行这个动作，观察结果（新的状态、奖励等），并将这些信息存储在经验回放缓冲区中。
随机抽样学习：从经验回放缓冲区中随机抽取一批经验。这种随机抽样可以减少样本间的相关性，增强学习的稳定性。
更新Critic网络：使用抽样出来的经验来更新Critic网络。Critic网络通过比较预测的价值和实际获得的奖励来调整其参数，使预测更准确。
更新Actor网络：使用Critic网络的反馈来更新Actor网络。Actor网络的目标是选择能够带来最大预期回报的动作，因此它根据Critic网络的反馈调整自己的策略。
更新目标网络：为了增加学习过程的稳定性，DDPG使用了目标网络。这些网络的参数定期（而不是每步）更新为主网络的参数。这样可以保证学习过程中的目标保持一定的稳定性。
重复并迭代：重复上述过程，逐渐改善Actor和Critic网络的性能，直到算法性能达到一定的标准或者迭代次数达到预设的限制。

DDPG的核心思想是使用深度学习方法来逼近一个最优策略，同时通过经验回放和目标网络技术来解决数据相关性和学习过程中的不稳定问题，解决连续动作空间的问题。

适合场景

深度确定性策略梯度（DDPG）算法适用于以下条件：

连续动作空间:
- DDPG非常适合于动作空间是连续的问题。例如，控制机器人的关节角度或者车辆的加速度，这些动作可以取任何在一定范围内的值。
高维状态空间:
- DDPG可以处理具有高维状态空间的问题，尤其是当状态空间可以通过传感器数据如图像输入到深度神经网络时。
离散时间决策:
- DDPG适用于需要在离散时间点做决策的场景，即决策步骤是离散的，虽然动作本身是连续的。
需要策略梯度的场景:
- 当问题需要通过策略梯度方法来优化策略时，DDPG是一个适用的选择。这是因为DDPG结合了策略梯度和函数逼近的优点，可以处理高维动作空间。
长期依赖的任务:
- 对于需要考虑长期回报的任务，DDPG通过使用时间差分（TD）学习和贝尔曼方程，可以有效地学习策略。
充分的计算资源:
- DDPG算法需要足够的计算资源来训练深度神经网络，这通常意味着有高性能的CPU/GPU和足够的内存。
稳定的环境模型:
- DDPG算法假设环境是固定不变的，或者变化是相对缓慢的，这样学习到的策略才能在实际环境中有效。
足够的探索机会:
- 由于DDPG是一种基于梯度的优化算法，它需要足够的探索机会来避免陷入局部最优。这通常通过噪声添加机制来实现，如在算法中使用