【数字图像处理技术与应用】2023-2024上图像处理期中-云南农业大学

一、填空题（每空2 分，共 30 分）

1、图像就是3D 场景在二维平面上的影像，根据其存储方式和表现形式，可以将图像分为模拟图像和数字图像两大类；

2、在用计算机对数字图像处理中，常用一个二维数组来存放图像数据，其大小与数字图像的大小一致(相同) ；

3、数字图像按存储格式可分为点位图和矢量(矢量图) ；

4、对于图像f(x, y)=xy2+3x ，它在点(x, y)处的梯度为▽f (x, y)= [y2+3,2xy] ；

5、图像数字化包括2 个过程：采样和量化；

6、傅立叶变换除了用于转换数字图像的图像信息，还能将微分方程转换成线性方程；

7、一幅基于3 基色 R,G,B 的 16 位颜色深度点位图，其颜色数量为 216 ；

8、 GIF 文件可以用来存储简单的动画，网页动画与QQ 表情就是借助它实现的；

9、可以通过阈值变换将一幅灰度图转换成黑白图；

10、一幅图形经过离散傅立叶变换后，低频信号集中于频域的中心(中心区域) ；

11、图像锐化的微分法，主要有梯度法和拉普拉斯法。

12、集合A={a ，b ，c} ，B={b ，c ，d} ，则集合 A⊕(异或)B= {a,b} 。

13、形态学图像处理中的开操作(Opening)A B ，相当于先用 B 对 A 进行腐蚀，然后用 B 对腐蚀结果进行膨胀；

二、判断题，正确打√ , 错误打 ⅹ（每题 1 分，共 10 分）

1、数字图像处理与图形学，研究的内容大致相同，方法也大致相同；( × )

2、饱和度是指颜色的纯度，即掺入白光的程度，指颜色的深浅程度；( √ )

3、傅立叶变换的结果是复数；( √ )

4、灰度图像的像素值只能是0 或 1； ( × )

5、伪彩色图像是灰度图象经过伪彩色处理后得到的，其目的是为了增强图像的视觉效果；( × )

6、图像锐化，经常采用卷积模板进行数字化处理，以提高处理速度和程序的通用性；( √ )

7、灰度线性变换的变换曲线，当斜率倾角小于45 度时，是扩展原图像的灰度动态范围；( × )

8、灰度线性变换中的削波变换，通常用于将灰度图像转换成黑白图；( × )

9、一维FFT 变换算法的时间复杂度为 N*log2N；( √ )

10、多图像平均法是利用同一景物的多幅图像取平均来消除噪声产生的高频成分。( √ )

三、简答题（每小题5 分，共 20 分）

1、试描述灰度图像与彩色图像的区别；

答：灰度图像在黑与白之间，有过渡灰色信息，但与彩色图像相比，仅有灰度和灰度的浓暗信息，没有颜色信息，以人眼对灰度的敏感程度，只能分辨约60 级左右的灰度信息，一般存储灰度像素信息仅需 1 字节 8 位二进制；彩色图像除了有灰度信息，还有颜色信息，计算机存储颜色信息通常采用 RGB 颜色模型。

2、下面左图是一张正常的女孩照片，右边是另一张对应女孩的直方图，请说出该直方图所对应女孩的照片的对比度和动态范围存在什么问题。

答：动态范围过窄，图像过暗；

3、请计算不定积分公式： ∫ ex sinxdx (偶数学号) ， ∫ ex cosxdx (奇数学号)

偶数学号：

$\int e^{x} \sin x \ dx = -e^{x} \cos x + \int e^{x} \cos x \, dx \\ -e^{x} \cos x + \left( e^{x} \sin x - \int e^{x} \sin x \, dx \right) \\ -e^{x} \cos x + e^{x} \sin x - \int e^{x} \sin x \, dx \\ -e^{x} \cos x + (e^{x} \sin x - \left( -e^{x} \cos x \right)/2$

奇数学号：

$\int e^{x} \cos x \, dx = e^{x} \sin x - \int e^{x} \sin x \, dx \\ e^{x} \sin x + \left( e^{x} \cos x - \int e^{x} \cos x \, dx \right) \\ e^{x} \sin x + (e^{x} \cos x + \left( -e^{x} \sin x \right)/2$

4 、根据以下的傅立叶变换蝶形单元，请推断 F(0)和 F(4)的计算公式。

答：以上蝶形运算单元的公式如下：

F(0)=G(0)+H(0)W08

F(4)=G(0)-H(0)W08

四、一副模拟彩色图像经平板扫描仪后获得一副彩色数字图像，其分辨率为1024×768 像素。若采用 RGB 彩色空间，红、绿、蓝三基色的灰度等级为 8bit，在无压缩的情况下，在计算机中存储该图像将占用多少BYTE 的存储空间？当用 PHOTOSHOP 图像处理软件去掉图像的彩色信息，只留下灰度信息，灰度等级为 8bit，在无压缩的情况下，存储图像将占用多少 bit 的存储空间？（5 分）

答：
(1)1024 x 768 x 8 x 3/8BYTE = 1024 x 768 x 3BYTE=3 x 768KB

(2)1024 x 768 x 8bit

五、利用右边半径为 1 的小圆对左边边长为 200 ，带有 2 个内孔的正方形施加膨胀运算，请画出膨胀运算后的图形。（5 分）

答：

六、请用左图的梯度算子模板给右图的 6x6 像素灰度图进行梯度锐化处理。（s 分）

答：

七、一原始图像共 8 个灰度级，其概率分布如下表：

灰度级 rk	r0=0	r1= 1/7	r2=2/7	r3=3/7	r4=4/7	r5=5/7	r6=6/7	r7= 1
像素数量 nk	790	1023	850	656	329	245	122	81
概率分布 P(rk)	0.19	0.25	0.21	0.16	0.08	0.06	0.03	0.02

原灰度级	变换函数 T(rk)值	像素数量	量化级	新灰度级及像素数量	新灰度级的像素概率分布
r0=0	T(r0)=S0=0.19	790	0		0
r1= 1/7	T(r1)=S1=	1023	1/7=0. 14	r0 → s1	0.19
r2=2/7	T(r2)=S2=	850	2/7=
r3=3/7	T(r3)=S3=	656	3/7=	r1 → s3	0.25
r4=4/7	T(r4)=S4=	329	4/7=
r5=5/7	T(r5)=S5=	245	5/7=	r2 → s5	0.21
r6=6/7	T(r6)=S6=	122	6/7=	r3 、r4 → s6	0.16+0.08
r7= 1	T(r7)=S7=	81	7/7= 1	r5 、r6 、r7 → s7	0.06+0.03+0.02

请仔细填写下图的直方图均衡化过程：（5 分）

答题要求：请在填表过程中，用箭头标明均衡化前后的灰度级对应关系；

注：1、原灰度级为 r0 、r1…r6 、r7 ，转换后的灰度级为：S0 ’、S1 ’、S2 ’…

2、直方图均衡化后，灰度级数量可能会较均衡化以前减少；

八、(C 语言版)请写一 C 代码片断，实现一幅彩色图像灰度化的处理（10 分）

初始条件：1 、像素彩色信息已存储于数组

struct RGB {
    
    unsigned char R;

    unsigned char G;

    unsigned char B;

};

struct RGB A[128][128]中；

2 、转换后的图像信息应存储于数组 unsigned char B[128][128]中；

答题要求：1 、请按要求的初始条件写出彩色图像灰度化的处理代码，不必写主函数，只需写出符合题目

要求的关键代码；

注意事项：1 、如果照抄实验代码，与题目所给的原始图像数组和处理后的图像信息数组不符，不能给分；

答：

#include <stdint.h>

// 定义RGB结构体，用于存储彩色像素的RGB值
struct RGB {
    unsigned char R; // 红色分量
    unsigned char G; // 绿色分量
    unsigned char B; // 蓝色分量
};

// 假设A数组已经填充了彩色图像的像素数据
struct RGB A[128][128];
// B数组用于存储灰度图像数据
unsigned char B[128][128];

// 将彩色图像转换为灰度图像的函数
void convertToGrayscale() {
    for (int i = 0; i < 128; ++i) {
        for (int j = 0; j < 128; ++j) {
            // 计算RGB分量的平均值，得到灰度值
            unsigned char gray = (A[i][j].R + A[i][j].G + A[i][j].B) / 3;
            // 将计算出的灰度值赋给B数组，存储灰度图像信息
            B[i][j] = gray;
        }
    }
}

// 注意：convertToGrayscale函数假设A数组已经用图像数据填充。
// 在主程序中初始化A数组后，调用此函数。

(Python 语言版)请写一 Python 代码片断，实现一幅彩色图像的灰度化处理（10 分）

import cv2

img = cv2.imread('2.jpg', 1)

i=j=0

sp=img.shape

#请在此处填写彩色图像灰度化的处理代码，包括循环语句

cv2.imshow('image',img)

注：1 、读取的彩色图形文件为 2.jpg ，读取的图像信息存储于对象数组 img ，已经是彩色图像信息；

2 、图像 x 方向分辨率为 sp[0],y 方向分辨率为 sp[1] ，转换后的阈值化图形存储在 img；

3 、坐标(x,y)的像素的颜色信息存储于 img[x][y] ，其中 img[x][y][0]是蓝色，img[x][y][1]是绿色，

img[x][y][2]是红色；

答：

import cv2
import numpy as np

# 读取彩色图像
img = cv2.imread('2.jpg', 1)

# 获取图像的尺寸
sp = img.shape

# 循环处理每个像素
for x in range(sp[0]):
    for y in range(sp[1]):
        # 获取像素的BGR颜色值
        (b, g, r) = img[x, y]
        # 计算灰度值，这里使用常见的加权平均法
        gray = int(0.299 * r + 0.587 * g + 0.114 * b)
        # 设置像素为灰度值
        img[x, y] = (gray, gray, gray)

# 在窗口中显示灰度化后的图像
cv2.imshow('Grayscale Image', img)

# 等待按键后关闭窗口
cv2.waitKey(0)
cv2.destroyAllWindows()

九、(C 语言版)请写一 C 代码片断，实现一幅灰度图像的阈值化处理（10 分）

初始条件：1 、像素灰度信息已存储于数组 unsigned char A[128][128]中；

2 、转换后的图像信息应存储于数组 unsigned char B[128][128]中；

3 、阈值 a= 120 ，灰度大于阈值时，灰度取 220 ，小于阈值时，灰度取 0；

答题要求：1 、请按要求的初始条件写出灰度图像的阈值化处理代码，不必写主函数，只需写出符合题目

要求的关键代码；

答：

unsigned char A[128][128]; // 假设这是输入的灰度图像
unsigned char B[128][128]; // 输出的图像
int i, j;
unsigned char a = 120; // 阈值

for(i = 0; i < 128; i++) {
    for(j = 0; j < 128; j++) {
        if(A[i][j] > a)
            B[i][j] = 220; // 灰度大于阈值时，灰度取220
        else
            B[i][j] = 0;   // 灰度小于等于阈值时，灰度取0
    }
}

2 、请绘出该灰度线性变换的变换曲线。

答：

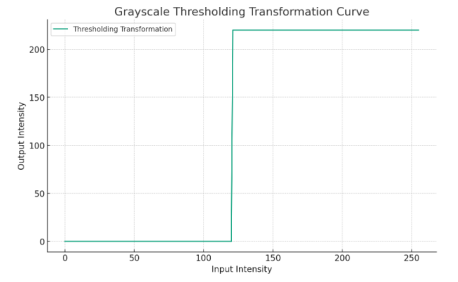
注意事项：1 、如果照抄实验代码，与题目所给的原始图像数组和处理后的图像信息数组不符，不能给分；

(Python 语言版)请写一 Python 代码片断，实现一幅灰度图像的阈值化处理（10 分）

以下是代码片段，请填写 Python 版的灰度图像阈值化处理的代码：

import cv2

img = cv2.imread('2.jpg', 1)

i=j=0

sp=img.shape

#请在此处填写灰度图像的阈值化代码，包括循环语句

cv2.imshow('image',img)

注：1 、阈值 a= 120 ，灰度大于阈值时，灰度取 220 ，小于阈值时，灰度取 0；

2 、读取的灰度图形文件为 2.jpg ，读取的图像信息存储于对象数组 img ，已经是灰度图像，其 R ，G，B 的灰度值均相等，即 R=G=B；

3 、图像 x 方向分辨率为 sp[0],y 方向分辨率为 sp[1] ，转换后的阈值化图形存储在 img；

答：

import cv2
img = cv2.imread('2.jpg', 0)  # 以灰度模式读取图像【灰度阈值变换曲线、阈值变换、输入强度、输出强度】
threshold = 120  # 设置阈值
sp = img.shape  # 获取图像的尺寸
# 应用阈值化处理
for i in range(sp[0]):
    for j in range(sp[1]):
        if img[i, j] > threshold:
            img[i, j] = 220
            else:
            img[i, j] = 0
            cv2.imshow('Thresholded Image', img)
            cv2.waitKey(0)# 显示阈值化后的图像
cv2.destroyAllWindows()