队列这种数据结构大都服务于一个算法——宽搜(BFS)。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等
N叉数的层序遍历
N叉树的层序遍历
题目解析
- 给定一个 N 叉树,返回其节点值的_层序遍历_。(即从左到右,逐层遍历)。
- 树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
算法原理
层序遍历(BFS宽度优先遍历):当我们遍历完 1、3、2、4时,要回过头看拓展3的子节点情况。这一过程属于先进先出的——队列这一数据结构可以解决,以二维数组的形式返回。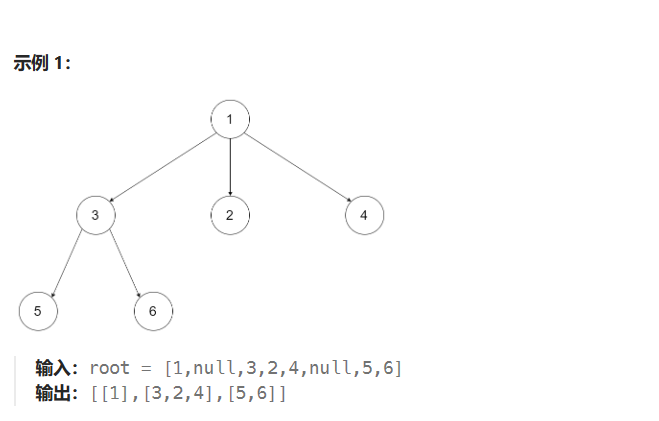
- 搞一个队列,如果根节点不为空,先让根节点入队。然后开始while循环,当队列不空的时候,把队头元素1拿出来,让队头元素的子节点2、3、4入队。接着继续将队头元素拿出来,让队头元素2的子节点5、6入队.接着将队头元素3拿出来,7入队,4拿出来,8入队。。继续拿出5、6、7、8(他们都没有子节点,就直接拿出即可)

· 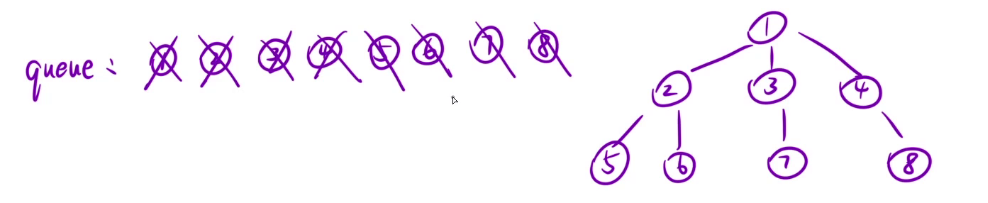
- 这里还有一个问题,在一次访问遍历节点时,如果出现不同层的节点元素进入,该怎样统计呢?我们这里只需要设置一个变量,统计元素个数。即当1进入队列时,计数为1;当1出队列时,2、3、4进入。此时个数为3就令变量为3。第二层出完时。第三层四个元素已经全部进入,令变量为4。
代码实现
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution
{
public:
vector<vector<int>> levelOrder(Node* root)
{
vector<vector<int>> ret; // 记录最终结果
queue<Node*> q; // 层序遍历需要的队列
if(root == nullptr) return ret;
q.push(root);
while(q.size())
{
int sz = q.size(); // 先求出本层元素的个数
vector<int> tmp; // 统计本层的节点
for(int i = 0; i < sz; i++)
{
Node* t = q.front(); //拿出队头元素
q.pop();
tmp.push_back(t->val); //将节点加入到最终返回的数组中
for(Node* child : t->children) // 遍历它的子节点,让下⼀层结点⼊队
{
if(child != nullptr)
q.push(child);
}
}
ret.push_back(tmp);
}
return ret;
}
};
二叉树的锯齿形层序遍历
二叉树的锯齿形层序遍历
题目解析
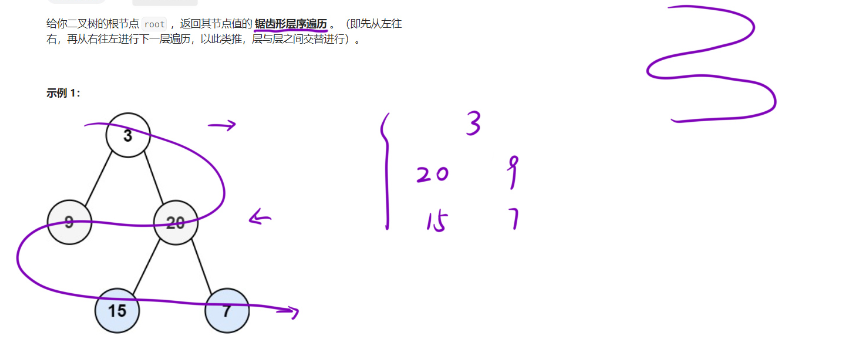
算法原理
解法:层序遍历
在层序遍历的结果存到最终返回结果之前,奇数行直接存入要返回的ret里,偶数行多执行一个逆序返回到ret里面即可。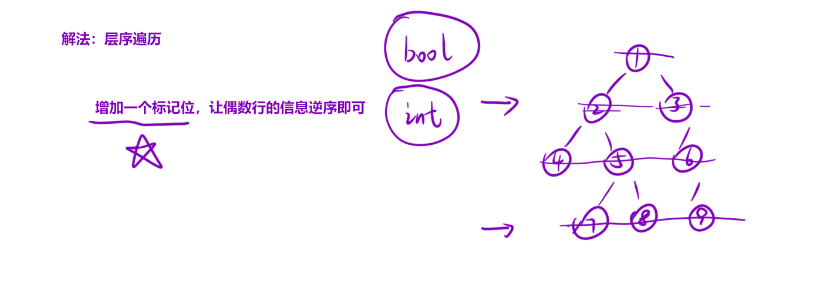
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root)
{
vector<vector<int>> ret;
if(root == nullptr) return ret;
queue<TreeNode*> q;
q.push(root);
int level = 1;
while(q.size())
{
int sz = q.size();
vector<int> tmp;
for(int i = 0; i < sz; i++)
{
auto t = q.front();
q.pop();
tmp.push_back(t->val);
if(t->left) q.push(t->left);
if(t->right) q.push(t->right);
}
// 判断是否逆序
if(level % 2 == 0) reverse(tmp.begin(), tmp.end());
ret.push_back(tmp);
level++;
}
return ret;
}
};
二叉树最大宽度
二叉树最大宽度
题目解析
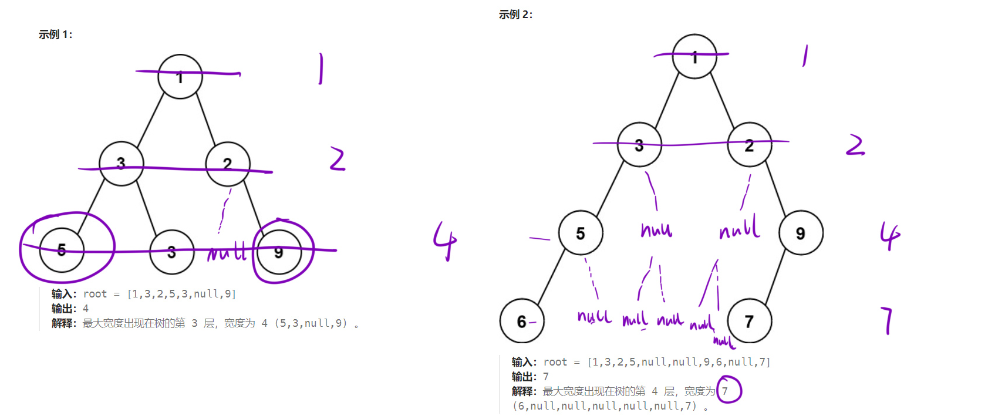
- 给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
- 树的 最大宽度 是所有层中最大的 宽度 。
- 每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
算法原理
解法一:硬来层序遍历
统计每⼀层的最⼤宽度,我们优先想到的就是利⽤层序遍历,把当前层的结点全部存在队列⾥⾯,利⽤队列的⻓度来计算每⼀层的宽度,统计出最⼤的宽度。但是,由于空节点也是需要计算在内的。因此,我们可以选择将空节点也存在队列⾥⾯。
当遍历到最后一层时,最后一层宽度为7。可以定义一个empty(统计null个数),从最后一层第一个位置开始扫描,遇到null节点+1,直至遇到下一个有效数字。停止,计算出宽度。然后再将empty置空为0,然后继续向后遍历,因为后面没有真实数字节点,所以最后一个null不计入宽度里。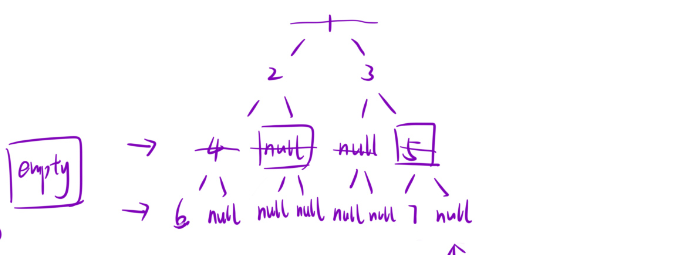
但是这里会超时,会有一种极端情况。将3000个节点平均分(题中给的数据范围为3000),如果还按照我们上述计算宽度的算法,那么最后一层将达到21000,这样是大大超出内存的。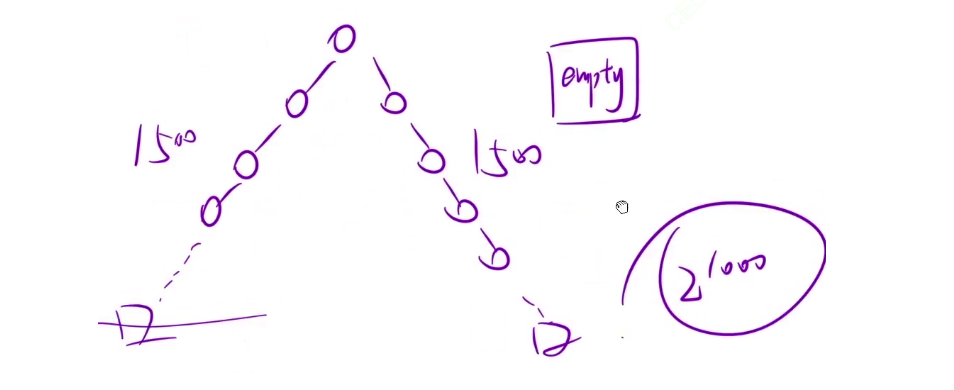
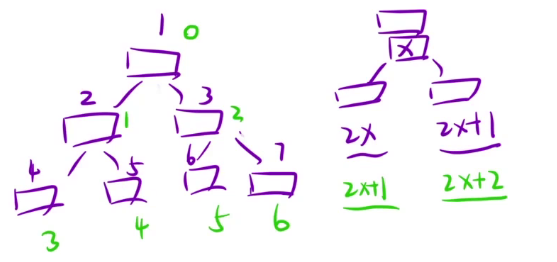
解法二:利用数组存储二叉树,给节点编号
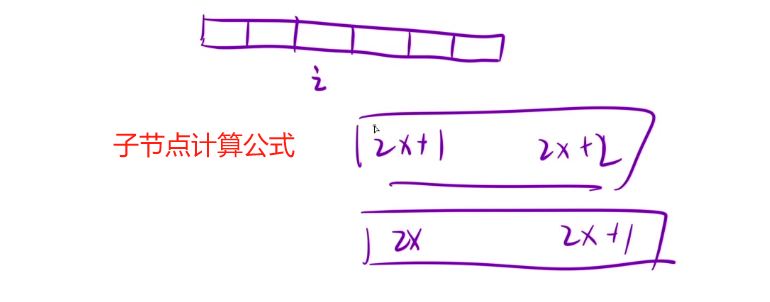
树我们不仅有链式存储,还有顺序存储。我们可以通过给二叉树节点编号,通过公式计算给他的子节点编号(两个公式区别就是头结点从1开始计数还是从0开始计数)
-
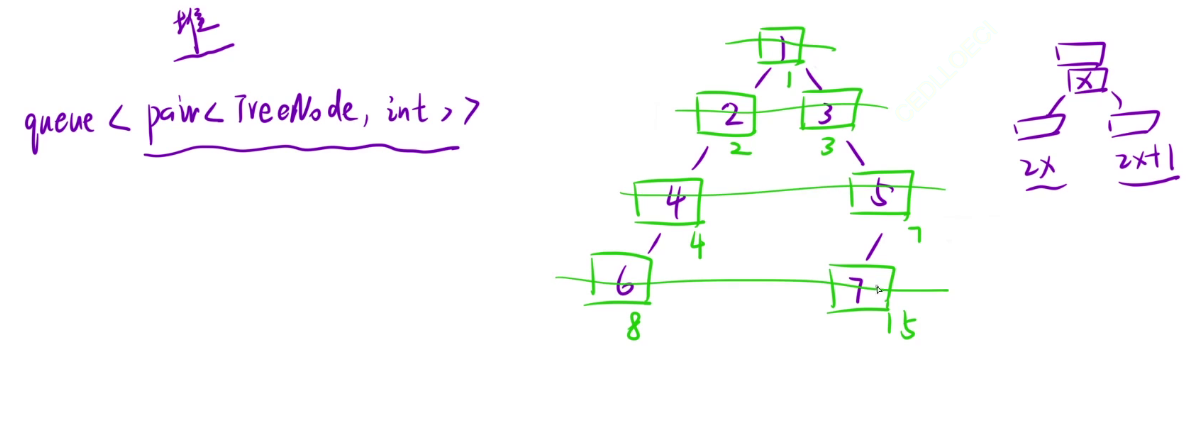
创建一个队列,此时队列里就不仅仅存储节点,我们即存他的节点,也存他的编号。计算宽度方法就是拿出这个队的队头,拿出这个队的对尾,下标相减+1即可;这样就不需要处理空节点了。(有的容器只能访问队头,不能访问队尾,这对于计算宽度就有些麻烦,我们可以用数组模拟队列)
-
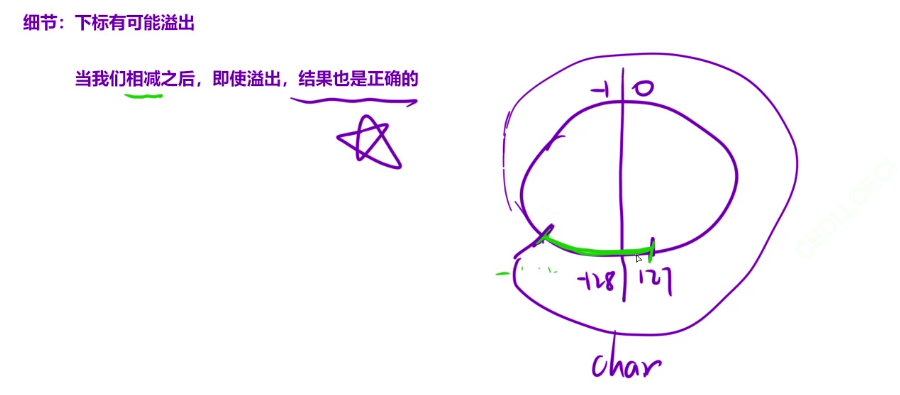
细节问题:下标有可能溢出。再次回到解法一遇到的极端情况,在那种情况下,最后一层的最后一个节点编号为21500-1.这个数字是任何一个数据类型都存不下的。但是当我们相减之后算出最后结果也是正确的。因为我们的数据存储是一个环形存储,我们最终计算的是距离(绿色部分),这个距离是不会溢出的,所以结果是正确的。我们C++用unsigned int存储就不会报错了
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
int widthOfBinaryTree(TreeNode* root)
{
vector<pair<TreeNode*, unsigned int>> q; // ⽤数组模拟队列
q.push_back({root, 1});
unsigned int ret = 0;
while(q.size())
{
// 先更新这⼀层的宽度
auto& [x1, y1] = q[0];
auto& [x2, y2] = q.back();
ret = max(ret, y2 - y1 + 1);
// 让下⼀层进队
vector<pair<TreeNode*, unsigned int>> tmp; // 让下⼀层进⼊这个队列
for(auto& [x, y] : q)
{
if(x->left) tmp.push_back({x->left, y * 2});
if(x->right) tmp.push_back({x->right, y * 2 + 1});
}
q = tmp;
}
return ret;
}
};
在每个树行中找最大值
在每个树行中找最大值
题目解析
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
算法原理
利用层序遍历,统计出每一层的最大值。
代码实现
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution
{
public:
vector<int> largestValues(TreeNode* root)
{
vector<int> ret;
if(root == nullptr) return ret;
queue<TreeNode*> q;
q.push(root);
while(q.size())
{
int sz = q.size();
int tmp = INT_MIN; //初始化为无穷小,让数字与tmp比较
for(int i = 0; i < sz; i++)
{
auto t = q.front(); //拿出队头元素
q.pop(); //干掉队头元素
tmp = max(tmp, t->val); //更新这一层最大值
if(t->left) q.push(t->left); //让其子节点入队
if(t->right) q.push(t->right);
}
ret.push_back(tmp);
}
return ret;
}
};