| 子环 | 环同态 | 理想 | |
|---|---|---|---|
| 单位元(乘法单位元) | 环与子环的单位元无必然关系,即子环不一定有单位元,有也不一定和环的单位元相同 比如 Z 6 Z_6 Z6有单位元1,其子环 ( 2 ) (2) (2)单位元为4;Z有单位元1,其子环2Z没有单位元 | 若R有单位元,则 I m R ImR ImR也有单位元,且 I m R ImR ImR的单位元为f(1)(同态满射) | 环与子环的单位元无必然关系。即子环不一定有单位元,有也不一定和环的单位元相同 |
| 零元(加法单位元) | 保持存在且不变 | 保持存在且不变 | 保持存在且不变 |
| 零因子 | 无关 | 同构映射下,零因子保持(若 a a a为 G G G的零因子,则 F ( a ) 为 G ′ F(a)为G' F(a)为G′的零因子),但是在普通环同态下没啥关系 | 无关 |
- 零元保持不变是因为它是加法的单位元,而环 R R R关于加法是做成群的,众所周知群的性质是相当优秀的,无论在子群还是群同态下都保持单位元
- 理想一定是子环,只是在此基础上满足了强吸收性,所以子环的性质它都满足。
环的基本性质
零因子:
环
R
R
R中必定存在0元(关于加法的群的单位元),对于
a
≠
0
∈
R
,
若
∃
b
≠
0
,
S
.
T
.
a
b
=
0
a\neq 0\in R,若\exist b\neq 0,S.T. ab=0
a=0∈R,若∃b=0,S.T.ab=0
则
a
a
a是环
R
R
R的左零因子。同理可以定义环
R
R
R的右零因子。
若 a a a既是环 R R R的左零因子,又是环 R R R的右零因子,它就是环 R R R的零因子。
1.1
如果一个环 R R R有左零因子,它也一定有右零因子
Proof:
注意到若 a ≠ 0 ∈ R a\neq 0\in R a=0∈R是左零因子,则 ∃ b ≠ 0 , a b = 0 \exist b\neq 0,ab=0 ∃b=0,ab=0,故 b b b是 R R R的右零因子。 □ \square □
该结论将左右零因子的地位反过来也是同理的。
1.2
R R R为无零因子环 ⇔ R \Leftrightarrow R ⇔R中关于乘法的左(右)消去律成立(此处消去律是针对非零元的)
Proof:
⇐ : \Leftarrow: ⇐:
若 R R R中左消去律成立。若 a ≠ 0 a\neq 0 a=0,有 a b = 0 ab=0 ab=0,则 a ∗ b = 0 = a ∗ 0 a*b=0=a*0 a∗b=0=a∗0,故由左消去律知 b = 0 b=0 b=0,故 R R R中没有左零因子,同理可得 R R R中没有右零因子。
⇒ : \Rightarrow: ⇒:
设环 R R R无左零因子。若有 a b = a c ab=ac ab=ac,则 a b − a c = a ( b − c ) = 0 ab-ac=a(b-c)=0 ab−ac=a(b−c)=0, a ≠ 0 a\neq 0 a=0时,由 R R R无左零因子,故 b − c = 0 b-c=0 b−c=0,即 b = c b=c b=c,左消去律得证。
由环 R R R无左零因子,故 R R R也没有右零因子,同理得右消去律成立 □ \square □
由此我们马上就知道:
1.3
环 R R R中左右消去律等价
这是因为左消去律成立,就能知道 R R R是无零因子环,从而 R R R满足右消去律。反之同理。
单位元:
定义为环 R R R关于乘法的群的单位元。
即
若
e
为
R
的单位元,则
∀
x
∈
R
,
e
x
=
x
e
=
x
若e为R的单位元,则\forall x\in R,ex=xe=x
若e为R的单位元,则∀x∈R,ex=xe=x
一般默认
e
≠
0
e\neq 0
e=0
可逆元:
对于 a ∈ R a\in R a∈R,若 ∃ b ∈ R , S . T . \exist b\in R,S.T. ∃b∈R,S.T. a b = b a = e ab=ba=e ab=ba=e,则 a a a是环 R R R的可逆元
可逆元与零元
Z n 中的可逆元与零元 Z_n中的可逆元与零元 Zn中的可逆元与零元
1.4
x ˉ \bar{x} xˉ为 Z n Z_n Zn的可逆元 ⇔ \Leftrightarrow ⇔ ( x , n ) = 1 (x,n)=1 (x,n)=1
Proof:
x ˉ \bar{x} xˉ为 Z n Z_n Zn的可逆元 ⇔ \Leftrightarrow ⇔ ∃ y ˉ ∈ R , x y ≡ 1 ( m o d n ) \exist \bar{y}\in R,xy\equiv 1(mod n) ∃yˉ∈R,xy≡1(modn) ⇔ \Leftrightarrow ⇔ ∃ k ∈ Z , x y + k n = 1 \exist k\in Z,xy+kn=1 ∃k∈Z,xy+kn=1 ⇔ \Leftrightarrow ⇔ ( x , n ) = 1 (x,n)=1 (x,n)=1
□ \square □
1.5
x ˉ \bar{x} xˉ为 Z n Z_n Zn的零因子 ⇔ \Leftrightarrow ⇔ ( x , n ) ≠ 1 (x,n)\neq 1 (x,n)=1
Proof:
考虑
n
=
∏
i
=
1
k
p
i
α
i
,
x
=
∏
i
=
1
d
q
i
β
i
n=\prod_{i=1}^{k} p_i^{\alpha_i},x=\prod_{i=1}^{d}q_i^{\beta_i}
n=i=1∏kpiαi,x=i=1∏dqiβi
若
(
x
,
n
)
=
d
>
1
(x,n)=d>1
(x,n)=d>1,则
x
(
n
/
d
)
≡
0
(
m
o
d
n
)
x(n/d)\equiv 0(mod n)
x(n/d)≡0(modn),故
x
x
x为
Z
n
Z_n
Zn的零因子
反之,若 x x x为 Z n Z_n Zn的零因子,则 ∃ d , x d ≡ 0 ( m o d n ) \exist d,xd\equiv 0(mod n) ∃d,xd≡0(modn),即 n ∣ x d n|xd n∣xd
若 ( x , n ) = 1 (x,n)=1 (x,n)=1,则 n ∣ d n|d n∣d,这与 d < n d<n d<n矛盾。故 ( x , n ) > 1 (x,n)>1 (x,n)>1
□ \square □
从而,我们得知,在环 Z n Z_n Zn中, 零因子与可逆元交集为空。这不是偶然
1.6
环 R R R的可逆元一定不是零因子
Proof:
若 a a a为环 R R R的可逆元,且 a a a为零因子,则 ∃ b ≠ 0 , a b = 0 = a 0 \exist b\neq 0,ab=0=a0 ∃b=0,ab=0=a0,又 a a a为可逆元,由左消去律知 b = 0 b=0 b=0,这与 b ≠ 0 b\neq 0 b=0矛盾。
□ \square □
若 a a a同时为可逆元,零因子,则与上述结论矛盾。故得可逆元一定不是零因子,零因子一定不是可逆元。
由证明过程不难得到如下推论:
1.6.2
环 R R R的左右零因子一定不是可逆元
Z n Z_n Zn的例子仿佛告诉我们虽然两者交集为空,但是覆盖了所有非零元。但是
1.7
事实上两者并不一定覆盖所有非零元。
比如环 2 Z 2Z 2Z没有零因子(毕竟 Z Z Z都没有),但是也没有单位元,自然也没有可逆元的说法。
不过事实上在 R R R为有单位元的有限环的时候还是有点关系的。
1.8
在有单位元的有限交换环 R R R中,任一不是零因子的非零元一定是可逆元
Proof:
可以设 R = { a 1 , a 2 , . . . a n } R=\{a_1,a_2,...a_n\} R={a1,a2,...an},若 a i ≠ 0 a_i\neq 0 ai=0,且不为零因子,则 a i R = { a i a 1 , a i a 2 , . . . a i a n } a_iR=\{a_ia_1,a_ia_2,...a_ia_n\} aiR={aia1,aia2,...aian}的元素两两不等(若 a i a x = a i a y a_ia_x=a_ia_y aiax=aiay,则 a i ( a x − a y ) = 0 a_i(a_x-a_y)=0 ai(ax−ay)=0,由 a i a_i ai不为零因子,故 a x = a y a_x=a_y ax=ay,这与初始条件矛盾),故 ∣ a i R ∣ = ∣ R ∣ |a_iR|=|R| ∣aiR∣=∣R∣,又 a i R ⊆ R a_iR\subseteq R aiR⊆R
故 a i R = R a_iR=R aiR=R,故 ∃ a j ≠ 0 , a i a j = 1 \exist a_j\neq 0 ,a_ia_j=1 ∃aj=0,aiaj=1,故 a i a_i ai为 R R R的左逆元。
又 R R R交换,故 a j a i = 1 a_ja_i=1 ajai=1,从而 a i a_i ai为可逆元 □ \square □
整环:
有单位元,无零因子,交换的环
除环:
至少有两个元素,非零元关于乘法做成群的环
由定义可知除环一定有单位元,无零因子。(非零元关于乘法做成群,必定有单位元,也必定满足封闭性)
域:
交换除环
由除环性质可知,域在除环的基础上加了交换性,从而域一定是一个整环
1.9
有限整环是一个域
Proof:
显然只需证非零元关于乘法做成群即可,又只需证每一个元素可逆。这一点的证明与1.8的证明几乎一样。 □ \square □
需要注意的是,该证明显然只对有限环成立。
1.10
Z m Z_m Zm为域 ⇔ \Leftrightarrow ⇔ m为素数
Proof:
Z m Z_m Zm是一个域 ⇔ \Leftrightarrow ⇔ Z m Z_m Zm是一个整环 ⇔ \Leftrightarrow ⇔ Z m Z_m Zm无零因子 ⇔ \Leftrightarrow ⇔ m m m为素数
第二个等价符号是因为 Z m Z_m Zm本身已经满足可交换和有单位元的性质了
□ \square □
环的特征
设
R
R
R是一个环,如果存在最小的正整数
n
n
n,使得
∀
x
∈
R
,
n
x
=
0
\forall x\in R,nx=0
∀x∈R,nx=0
则称
n
n
n为环
R
R
R的特征,记为
C
h
R
ChR
ChR
若不存在这样的 n n n,称环 R R R的特征为无限
不难发现, C h R ChR ChR就是环内所有元素关于加法的阶的 L c m Lcm Lcm
1.11
若 R R R有单位元,则 C h R ChR ChR等于单位元1关于加法的阶 n n n
Proof:
显然 C h R ≥ ∣ 1 ∣ = n ChR\geq |1|=n ChR≥∣1∣=n。
∀ x ∈ R , n x = n ( 1 ∗ x ) = ( n 1 ) ∗ x = 0 ∗ x = 0 \forall x\in R,nx=n(1*x)=(n1)*x=0*x=0 ∀x∈R,nx=n(1∗x)=(n1)∗x=0∗x=0,故 ∣ x ∣ ∣ n |x|| n ∣x∣∣n
从而 C h R ≤ n ChR\leq n ChR≤n
从而 C h R = n ChR=n ChR=n □ \square □
1.12
若环 R R R无零因子,则 R R R中所有非零元关于加法的阶都相同,从而 C h R ChR ChR等于任意非零元的关于加法的阶。另外,此时** C h R ChR ChR为素数**
Proof:
若 R R R中所有元素的阶都是无限的,该结论显然正确。
否则
∃
x
∈
R
,
∣
x
∣
=
n
\exist x\in R,|x|=n
∃x∈R,∣x∣=n为一个有限正整数。从而
n
x
=
0
nx=0
nx=0。此时
∀
y
≠
0
∈
R
,
x
∗
(
n
y
)
=
(
n
x
)
∗
y
=
0
∗
y
=
0
\forall y\neq 0 \in R,x*(ny)=(nx)*y=0*y=0
∀y=0∈R,x∗(ny)=(nx)∗y=0∗y=0
又环中无零因子,从而
n
y
=
0
ny=0
ny=0,从而
∣
y
∣
≤
∣
x
∣
|y|\leq |x|
∣y∣≤∣x∣
此时 ∣ y ∣ |y| ∣y∣也有限,我们交换一下x,y的位置马上得到: ∣ y ∣ ≥ ∣ x ∣ |y|\geq |x| ∣y∣≥∣x∣
从而 ∣ x ∣ = ∣ y ∣ |x|=|y| ∣x∣=∣y∣。从而 R R R中所有非零元关于加法的阶都相同。
接下来证明第二个子结论。若 ∃ 1 < k , t < n ∈ Z , k ∗ t = n \exist 1<k,t<n\in Z,k*t=n ∃1<k,t<n∈Z,k∗t=n,即 n n n为一个合数,
∀
x
∈
R
∗
,
x
2
∈
R
\forall x\in R^{*},x^2\in R
∀x∈R∗,x2∈R,从而
∣
x
∣
=
∣
x
2
∣
=
n
|x|=|x^2|=n
∣x∣=∣x2∣=n,故
0
=
n
∗
x
2
=
k
t
∗
x
2
=
(
k
x
)
(
t
x
)
=
0
0=n*x^{2}=kt*x^{2}=(kx)(tx)=0
0=n∗x2=kt∗x2=(kx)(tx)=0
又
R
R
R没有零因子,故
k
x
=
0
或
t
x
=
0
kx=0或tx=0
kx=0或tx=0,这与
∣
x
∣
=
n
|x|=n
∣x∣=n矛盾。
从而 n n n为素数
□ \square □
不难得到以下推论
1.13
整环的特征为素数,从而域的特征为素数
子环
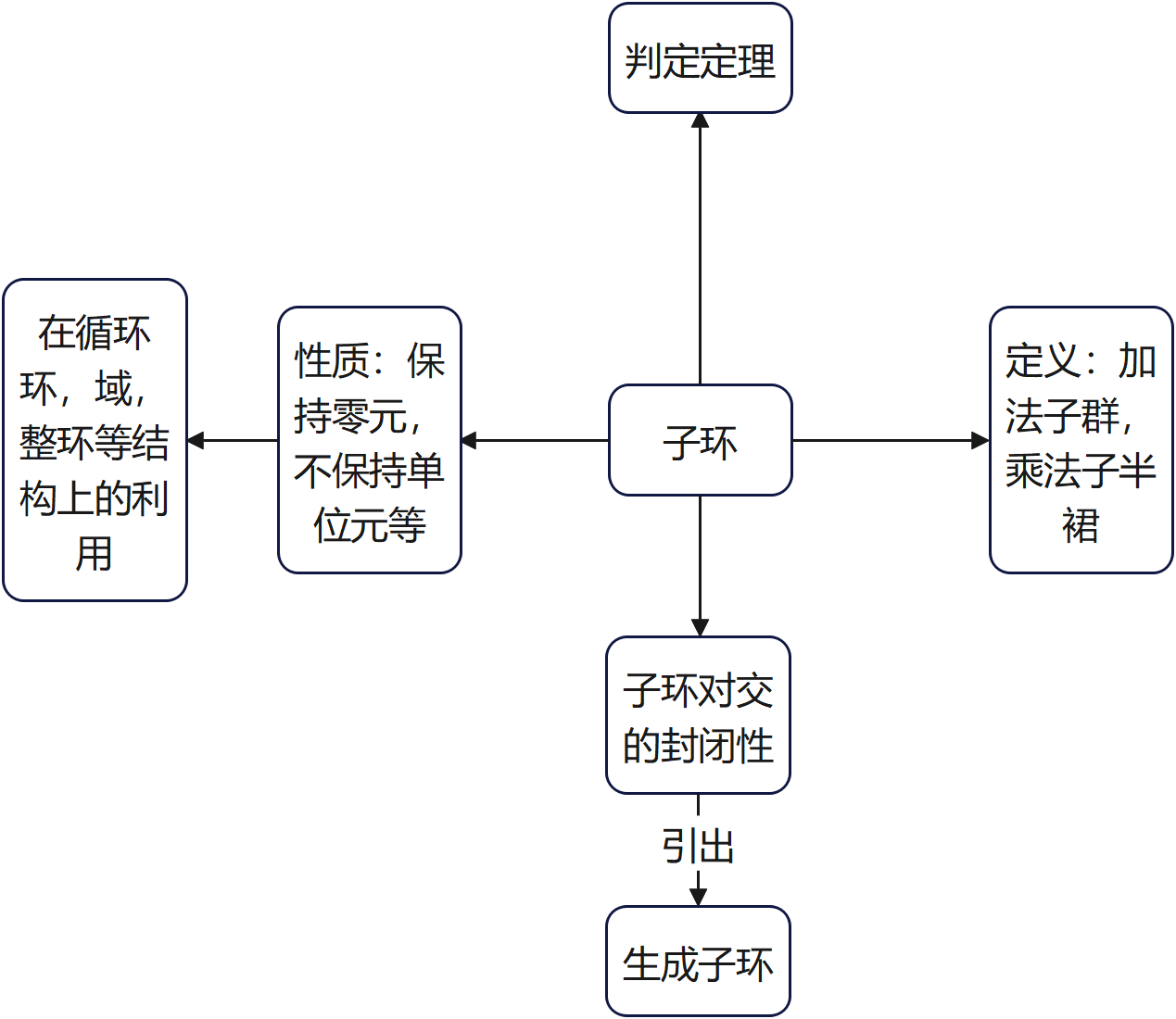
定义:
设 S S S是环 R R R的非空子集,若 S S S关于 R R R的加法,乘法也做成环,则 S S S是环 R R R的子环
判定
2.1
若 S S S是环 R R R的非空子集,则 S S S是 R R R的子环的充要条件:
KaTeX parse error: No such environment: flalign at position 27: …b\in S\\ \begin{̲f̲l̲a̲l̲i̲g̲n̲}̲ &(1)a-b\in S,\…
Proof:
条件(1)与 S S S关于加法做成群等价。接下来证 S S S是半群即可。 R R R已经满足运算的合理性,结合律,我们只要封闭性即可。这一点由(2)保证,且是等价的。
□ \square □
循环环的子环:
2.2
循环环的子环 ⇔ \Leftrightarrow ⇔ 循环环的加法子群
Proof:
设 R = ( a ) = { k a ∣ k ∈ Z } R=(a)=\{ka|k\in Z\} R=(a)={ka∣k∈Z}为循环环
⇐ : \Leftarrow: ⇐:
S
S
S为
R
R
R的子群,则
∃
l
∈
Z
,
S
=
(
l
a
)
=
{
k
(
l
a
)
∣
k
∈
Z
}
\exist l\in Z,S=(la)=\{k(la)|k\in Z\}
∃l∈Z,S=(la)={k(la)∣k∈Z},从而
∀
k
1
(
l
a
)
,
k
2
(
l
a
)
∈
R
,
k
1
(
l
a
)
∗
k
2
(
l
a
)
=
k
1
k
2
l
2
a
2
a
2
∈
R
,
故
∃
s
∈
Z
,
s
a
=
a
2
从而
k
1
(
l
a
)
∗
k
2
(
l
a
)
=
k
1
k
2
l
s
(
l
a
)
∈
(
l
a
)
=
S
\forall k_1(la),k_2(la)\in R,k_1(la)*k_2(la)=k_1k_2l^2a^2\\ a^2\in R,故\exist s\in Z,sa=a^2\\ 从而\\ k_1(la)*k_2(la)=k_1k_2ls(la)\in (la)=S
∀k1(la),k2(la)∈R,k1(la)∗k2(la)=k1k2l2a2a2∈R,故∃s∈Z,sa=a2从而k1(la)∗k2(la)=k1k2ls(la)∈(la)=S
故
S
S
S关于乘法封闭。显然
S
S
S关于加法做成群,故
S
S
S是
R
R
R的子环。
⇒ : \Rightarrow: ⇒:
显然
□ \square □
子环关于交的封闭性
2.3
环 R R R的若干个子环的交仍是子环。将子环换成子整环,子除环,子域显然也是正确的。
这个不证了。
从而我们可以引出生成子环的概念。至于为什么生成子环是由该性质引出的,看证明就能明白。
生成子环
设
T
T
T是
R
R
R的一个非空子集,若
R
R
R的子环
S
S
S满足
(
1
)
T
⊆
S
(
2
)
∀
S
′
<
R
且
T
⊆
S
′
,
S
⊆
S
′
(1) T\subseteq S\\ (2) \forall S'<R且T\subseteq S',S\subseteq S'
(1)T⊆S(2)∀S′<R且T⊆S′,S⊆S′
则
S
S
S称为
T
T
T生成的子环,记为
S
=
[
T
]
S=[T]
S=[T]
2.4 生成子环的存在性
Proof:
我们需要对于一个集合 T T T,其生成子环总是存在的,并且满足上述性质。概括一下就是包含 T T T的最小子环。可以取所有包含 T T T的子环的交,先证其最小,再证其为子环。
记 { S i ∣ i ∈ I } \{S_i|i\in I\} {Si∣i∈I}为包含 T T T的子环集合。显然 T ⊆ R , R 为环 T\subseteq R,R为环 T⊆R,R为环,故 { S i ∣ i ∈ I } \{S_i|i\in I\} {Si∣i∈I}非空。
取
S
=
⋂
i
∈
I
S
i
,
S
S=\bigcap_{i\in I}S_i,S
S=⋂i∈ISi,S的最小性显然。注意到
∀
i
∈
I
,
T
⊆
S
i
\forall i\in I,T\subseteq S_i
∀i∈I,T⊆Si
故
T
⊆
⋂
i
∈
I
S
i
=
S
T\subseteq \bigcap_{i\in I}S_i=S
T⊆i∈I⋂Si=S
又
S
S
S是若干个子环的交,故
S
S
S是一个子环。从而
S
S
S是包含
T
T
T的最小子环,
S
=
[
T
]
S=[T]
S=[T]
存在性得证,且
[
T
]
=
⋂
i
∈
I
S
i
[T]=\bigcap_{i\in I}S_i
[T]=i∈I⋂Si
□
\square
□
生成子环[T]的元素形式
任取
t
1
,
t
2
,
.
.
.
t
k
∈
T
t_1,t_2,...t_k\in T
t1,t2,...tk∈T,则
±
t
1
t
2
.
.
.
t
k
∈
[
T
]
\pm t_1t_2...t_k\in [T]
±t1t2...tk∈[T]
从而由子环对加法的封闭性知
{
∑
±
t
1
t
2
.
.
.
t
k
∣
t
i
∈
T
,
k
∈
Z
+
}
⊆
[
T
]
\{\sum \pm t_1t_2...t_k|t_i\in T,k\in Z^{+}\}\subseteq [T]
{∑±t1t2...tk∣ti∈T,k∈Z+}⊆[T]
又不难证明
{
∑
±
t
1
t
2
.
.
.
t
k
∣
t
i
∈
T
,
k
∈
Z
+
}
是一个子环
\{\sum \pm t_1t_2...t_k|t_i\in T,k\in Z^{+}\}是一个子环
{∑±t1t2...tk∣ti∈T,k∈Z+}是一个子环
且显然它包含
T
T
T。由
[
T
]
[T]
[T]的最小性可知
[
T
]
⊆
{
∑
±
t
1
t
2
.
.
.
t
k
∣
t
i
∈
T
,
k
∈
Z
+
}
[T]\subseteq \{\sum \pm t_1t_2...t_k|t_i\in T,k\in Z^{+}\}
[T]⊆{∑±t1t2...tk∣ti∈T,k∈Z+}
从而
[
T
]
=
{
∑
±
t
1
t
2
.
.
.
t
k
∣
t
i
∈
T
,
k
∈
Z
+
}
[T]= \{\sum \pm t_1t_2...t_k|t_i\in T,k\in Z^{+}\}
[T]={∑±t1t2...tk∣ti∈T,k∈Z+}
这就是生成子环
[
t
]
[t]
[t]的元素形式。
2.5
当 T = { a } T=\{a\} T={a}时,
[ T ] = { ∑ n i a i ∣ i ∈ Z + , n i ∈ Z } [T]=\{\sum n_ia^{i}|i\in Z^{+},n_i\in Z\} [T]={∑niai∣i∈Z+,ni∈Z}
环同态
其实与群同态是类似的,要求映射满足加法保持运算,乘法保持运算即可。
性质:
- 0元保持不变
- 像的逆等于逆的像
以上两条由加法群同态保证.若f是一个 R R R到 R ′ R' R′的满射,则
- 若 R R R是交换群,则 R ′ R' R′也是交换群
- 若 R R R有单位元1,则 R ′ R' R′也有单位元 f ( 1 ) f(1) f(1)
以上四条的逆均未必成立。
3.1
构造 Z n Z_n Zn到 Z m Z_m Zm的环同态
Start:
环同态首先是群同态,由此我们需要满足:
(
1
)
f
(
0
)
=
0
(
2
)
n
f
(
1
)
≡
0
(
m
o
d
m
)
(1) f(0)=0\\ (2) nf(1)\equiv 0(mod m)
(1)f(0)=0(2)nf(1)≡0(modm)
此时只需要保证
f
f
f关于乘法保持运算即可。
下面给出在加法满足群同态的情况下f关于乘法保持运算的充要条件:
f
(
1
)
≡
f
2
(
1
)
(
m
o
d
m
)
f(1)\equiv f^{2}(1)(mod m)
f(1)≡f2(1)(modm)
Proof:
⇐ : \Leftarrow: ⇐:
已知
f
(
1
)
≡
f
2
(
1
)
(
m
o
d
m
)
f(1)\equiv f^{2}(1)(mod m)
f(1)≡f2(1)(modm),
∀
x
,
y
∈
R
\forall x,y\in R
∀x,y∈R
f
(
x
y
)
=
f
(
(
1
+
1
+
.
.
.
+
1
)
⏟
x
个
∗
y
)
=
f
(
y
+
y
+
.
.
.
+
y
⏟
x
个
)
=
x
f
(
y
)
=
x
(
y
f
(
1
)
)
=
x
y
f
2
(
1
)
=
(
x
f
(
1
)
)
(
y
f
(
1
)
)
=
f
(
x
)
f
(
y
)
f(xy)=f(\underbrace{(1+1+...+1)}_{x个}*y)=f(\underbrace{y+y+...+y}_{x个}) \\=xf(y)=x(yf(1))=xyf^{2}(1)=(xf(1))(yf(1))=f(x)f(y)
f(xy)=f(x个
(1+1+...+1)∗y)=f(x个
y+y+...+y)=xf(y)=x(yf(1))=xyf2(1)=(xf(1))(yf(1))=f(x)f(y)
⇒
:
\Rightarrow:
⇒:
已知 ∀ x , y ∈ R , f ( x y ) = f ( x ) f ( y ) \forall x,y\in R,f(xy)=f(x)f(y) ∀x,y∈R,f(xy)=f(x)f(y)
带入 x = y = 1 x=y=1 x=y=1即得证。
□ \square □
从而,f是
Z
n
Z_n
Zn到
Z
m
Z_m
Zm的充要条件为:
(
1
)
f
(
0
)
=
0
(
2
)
n
f
(
1
)
≡
0
(
m
o
d
m
)
(
3
)
f
(
1
)
≡
f
2
(
1
)
(
m
o
d
m
)
(1) f(0)=0\\ (2) nf(1)\equiv 0(mod m)\\ (3) f(1)\equiv f^{2}(1)(mod m)
(1)f(0)=0(2)nf(1)≡0(modm)(3)f(1)≡f2(1)(modm)
End
理想

从理想开始就算是正式进入环论了。
定义
设
I
I
I是环
R
R
R的一个非空子集,若
(
1
)
∀
a
,
b
∈
I
,
a
−
b
∈
I
(
2
)
∀
a
∈
I
,
∀
b
∈
R
,
a
b
,
b
a
∈
I
(1) \forall a,b\in I,a-b\in I\\ (2) \forall a\in I,\forall b\in R,ab,ba\in I
(1)∀a,b∈I,a−b∈I(2)∀a∈I,∀b∈R,ab,ba∈I
则称
I
I
I是环
R
R
R的理想
显然理想必定是子环,但是子环不一定是理想。
任意一个非零环 R R R都含有 { 0 } 和 R \{0\}和R {0}和R本身这两个理想,它们称为平凡理想。除此之外的理想称为 R R R的真理想。
单环
4.1
设 R R R是一个有单位元的环, R R R的每一个真理想都不可能含有单位元
Proof:
设
I
I
I是
R
R
R的一个真理想。若
1
∈
I
1\in I
1∈I,则
∀
x
∈
R
,
x
=
1
∗
x
∈
I
\forall x\in R,x=1*x\in I
∀x∈R,x=1∗x∈I
从而
I
=
R
I=R
I=R,这与
I
I
I是
R
R
R的真理想矛盾。
□
\square
□
不含有真理想的环 R R R称为单环
4.2
除环,域都是单环
Proof:
设 I I I是域 F F F的一个真理想,则 ∃ x ∈ I , x ≠ 0 \exist x\in I,x\neq 0 ∃x∈I,x=0
从而 x ∈ I , x − 1 ∈ I , x x − 1 = 1 ∈ I x\in I,x^{-1}\in I,xx^{-1}=1\in I x∈I,x−1∈I,xx−1=1∈I,这与4.1的结论矛盾。(这里用到了 F ∗ F^{*} F∗是一个群,从而保证逆元存在,这一点除环和域是一样的)
从而 I I I不是 F F F的真理想。 □ \square □
4.3
设 R R R是一个有单位元 1 1 1的交换环。若 R R R没有非平凡的理想,则 R R R是一个域
Proof:
要证 R R R是一个域,我们现在只需要证明 R ∗ R^{*} R∗关于乘法做成群即可。如此只需要验证乘法封闭性以及每一个非零元的可逆性即可。
注意到可逆元一定不是非零元,从而保证了乘法封闭。
所以我们只需验证每一个元素可逆即可。
任取
a
∈
R
a\in R
a∈R,考虑
a
R
=
{
a
r
∣
r
∈
R
}
aR=\{ar|r\in R\}
aR={ar∣r∈R}
显然该集合关于加法做成群。且
∀
a
r
∈
a
R
,
x
∈
R
∃
d
∈
R
,
d
=
r
x
=
x
r
\forall ar\in aR,x\in R\\ \exist d\in R,d=rx=xr
∀ar∈aR,x∈R∃d∈R,d=rx=xr
从而
(
a
r
)
∗
x
=
a
∗
(
r
x
)
=
a
d
∈
a
R
x
∗
(
a
r
)
=
(
x
r
)
∗
a
=
a
d
∈
a
R
(ar)*x=a*(rx)=ad\in aR\\ x*(ar)=(xr)*a=ad\in aR
(ar)∗x=a∗(rx)=ad∈aRx∗(ar)=(xr)∗a=ad∈aR
故
a
R
aR
aR是
R
R
R的一个理想。又
R
R
R不含真理想,且
a
∈
a
R
a\in aR
a∈aR,从而
a
R
=
R
aR=R
aR=R
故
∃
x
∈
R
,
a
x
=
x
a
=
1
\exist x\in R,ax=xa=1
∃x∈R,ax=xa=1
从而
a
a
a可逆。由此我们证得每一个非零元都是可逆的。
故 R R R是一个域。 □ \square □
这种算是一个常见套路了。通过构造环的左陪集=环本身来证明元素的可逆性,这一点在这里和证明有限整环是域的时候都用过。只不过之前是用无零因子来证明相等,而这里使用无真理想来证明,实际上也推出了无零因子
从4.2和4.3我们不难得到下述结论
4.4
这 R R R是一个有单位元的交换环,则 R R R是域当且仅当 R R R没有非平凡理想,即 R R R是单环
证明从略。
理想关于交的封闭性
环 R R R的若干个理想的交仍是理想
证明从略。
理想它首先是一个子环,所以子环的很多结论它都是可以对应过来的。那么跟子环一样,我们同样在这里可以导出生成理想的概念
生成理想
设
T
T
T是环
R
R
R的一个非空子集,若存在
R
R
R的理想
I
I
I,使得
(
1
)
T
⊆
I
(
2
)
∀
I
′
是
R
的理想
,
且
T
⊆
I
′
,
有
I
⊆
I
′
(1) T\subseteq I\\ (2) \forall I'是R的理想,且T\subseteq I',有I\subseteq I'
(1)T⊆I(2)∀I′是R的理想,且T⊆I′,有I⊆I′
则
I
I
I称为集合
T
T
T的生成理想。记为
I
=
(
T
)
I=(T)
I=(T)
生成理想的存在性
我们很快注意到这一块跟子环是完全类似的。证明的思路也是一模一样。
先证包含 T T T的理想总是存在,再构造 I = ⋂ i ∈ I I i I=\bigcap_{i\in I}I_i I=⋂i∈IIi,其中 I i I_i Ii的意义就是包含 T T T的所有理想。证明 I I I的最小性和以及它是一个理想即可。
设 T = { a 1 , a 2 . . . . a n } T=\{a_1,a_2....a_n\} T={a1,a2....an},则记理想 ( T ) = ( a 1 , a 2 , . . . a n ) (T)=(a_1,a_2,...a_n) (T)=(a1,a2,...an).当 T = { a } T=\{a\} T={a}时,称 ( T ) = ( a ) (T)=(a) (T)=(a)为 a a a生成的主理想。
再来看看理想关于和的封闭性。
理想关于和的封闭性
4.5
设 I 1 , I 2 I_1,I_2 I1,I2为 R R R的两个理想,则 I 1 + I 2 I_1+I_2 I1+I2也是理想。
Proof:
∀
x
,
y
∈
I
1
+
I
2
,
∀
r
∈
R
\forall x,y\in I_1+I_2,\forall r\in R
∀x,y∈I1+I2,∀r∈R,记
x
=
x
1
+
x
2
,
y
=
y
1
+
y
2
x=x_1+x_2,y=y_1+y_2
x=x1+x2,y=y1+y2,其中
x
1
,
y
1
∈
I
1
,
x
2
,
y
2
∈
I
2
x_1,y_1\in I_1,x_2,y_2\in I_2
x1,y1∈I1,x2,y2∈I2.则
x
−
y
=
x
1
+
x
2
−
y
1
−
y
2
=
(
x
1
−
y
1
)
+
(
x
2
−
y
2
)
∈
I
1
+
I
2
r
x
=
r
(
x
1
+
x
2
)
=
r
x
1
+
r
x
2
∈
I
1
+
I
2
x
r
=
(
x
1
+
x
2
)
r
=
x
1
r
+
x
2
r
∈
I
1
+
I
2
x-y=x_1+x_2-y_1-y_2=(x_1-y_1)+(x_2-y_2)\in I_1+I_2\\ rx=r(x_1+x_2)=rx_1+rx_2\in I_1+I_2\\ xr=(x_1+x_2)r=x_1r+x_2r\in I_1+I_2\\
x−y=x1+x2−y1−y2=(x1−y1)+(x2−y2)∈I1+I2rx=r(x1+x2)=rx1+rx2∈I1+I2xr=(x1+x2)r=x1r+x2r∈I1+I2
从而
I
1
+
I
2
I_1+I_2
I1+I2是
R
R
R的理想
□
\square
□
进而得到下述结论:
4.6
设 a 1 , a 2 , . . a n ∈ R a_1,a_2,..a_n\in R a1,a2,..an∈R,
则 ( a 1 , a 2 , . . . a n ) = ( a 1 ) + ( a 2 ) + . . . + ( a n ) (a_1,a_2,...a_n)=(a_1)+(a_2)+...+(a_n) (a1,a2,...an)=(a1)+(a2)+...+(an)
**Proof: **
记 I 1 = ( a 1 , a 2 , . . . a n ) , I 2 = ( a 1 ) + ( a 2 ) + . . . + ( a n ) I_1=(a_1,a_2,...a_n),I_2=(a_1)+(a_2)+...+(a_n) I1=(a1,a2,...an),I2=(a1)+(a2)+...+(an)
∀ a i , a i ∈ ( a i ) ⊆ I 2 \forall a_i,a_i\in (a_i)\subseteq I_2 ∀ai,ai∈(ai)⊆I2
又 I 1 I_1 I1是包含所有 a i a_i ai的最小理想,故 I 1 ⊆ I 2 I_1\subseteq I_2 I1⊆I2
又 ( a i ) (a_i) (ai)是包含 a i a_i ai的最小理想,故 ∀ i ∈ [ 1 , n ] , ( a i ) ⊆ I 1 \forall i\in [1,n],(a_i)\subseteq I_1 ∀i∈[1,n],(ai)⊆I1
由理想对加法的封闭性, I 2 ⊆ I 1 I_2\subseteq I_1 I2⊆I1
故 I 1 = I 2 I_1=I_2 I1=I2 □ \square □
理想与主理想的关系
根据4.6,我们得到如下结论:
每一个理想都是若干个主理想之和
有了以上铺垫,我们就可以来探究生成理想的元素形式了。
生成理想的元素形式
由于4.6的结论,实际上我们只需要探究主理想的元素形式。
给出结论
在 R R R中, ( a ) = { ∑ x i a y i + s a + a t + n a ∣ x i , y i , s , t ∈ R , n ∈ Z } (a)=\{\sum x_iay_i+sa+at+na|x_i,y_i,s,t\in R ,n\in Z\} (a)={∑xiayi+sa+at+na∣xi,yi,s,t∈R,n∈Z}
4.7
若
R
R
R是一个有单位元的环,则
(
a
)
=
{
∑
x
i
a
y
i
∣
x
i
,
y
i
∈
R
}
(a)=\{\sum x_iay_i|x_i,y_i\in R\}
(a)={∑xiayi∣xi,yi∈R}
若
R
R
R是一个交换环,则
(
a
)
=
{
∑
r
a
+
n
a
∣
r
∈
R
,
n
∈
Z
}
(a)=\{\sum ra+na|r\in R,n\in Z\}
(a)={∑ra+na∣r∈R,n∈Z}
若
R
R
R是一个有单位元的交换环,则
(
a
)
=
{
r
a
∣
r
∈
R
}
=
a
R
=
R
a
(a)=\{ra|r\in R\}=aR=Ra
(a)={ra∣r∈R}=aR=Ra
循环环的理想:
在子环中已经讲过,循环环的子环等价于循环环关于加法的子群,事实上,循环环的子环也一定是理想,且为主理想。
4.8
循环环的理想都是主理想
设 I I I是循环环 R = ( a ) R=(a) R=(a)的理想,则 I I I也是 R R R的加法子群,故 I = ( s a ) I=(sa) I=(sa)
下证 I 就是 s a I就是sa I就是sa生成的主理想
s
a
sa
sa生成的主理想
<
s
a
>
=
{
r
(
s
a
)
+
n
(
s
a
)
∣
r
∈
R
,
n
∈
Z
}
<sa>=\{r(sa)+n(sa)|r\in R,n\in Z\}
<sa>={r(sa)+n(sa)∣r∈R,n∈Z}
显然
<
s
a
>
⊆
I
<sa>\subseteq I
<sa>⊆I
又
∀
x
=
m
(
s
a
)
∈
I
,
x
=
0
∗
(
s
a
)
+
m
∗
(
s
a
)
∈
<
s
a
>
\forall x=m(sa)\in I,x=0*(sa)+m*(sa)\in <sa>
∀x=m(sa)∈I,x=0∗(sa)+m∗(sa)∈<sa>
故
I
⊆
<
s
a
>
I\subseteq <sa>
I⊆<sa>
故 I = < s a > I=<sa> I=<sa> □ \square □
从而
在循环环中,子环 ⇔ \Leftrightarrow ⇔理想 ⇔ \Leftrightarrow ⇔主理想
4.9
设 f f f是 R R R到 R ′ R' R′的一个环同态满射。 I I I是环 R R R的子集, I ′ I' I′是环 R ′ R' R′的子集
则:
( 1 ) 若 I 是环 R 的理想,则 f ( I ) 是环 R ′ 的理想 ( 2 ) 若 I ′ 是环 R ’的理想,则 f − 1 ( I ′ ) 是环 R 的理想,且 K e r f ⊆ f − 1 ( I ′ ) (1) 若I是环R的理想,则f(I)是环R'的理想\\ (2) 若I'是环R’的理想,则f^{-1}(I')是环R的理想,且Kerf\subseteq f^{-1}(I') (1)若I是环R的理想,则f(I)是环R′的理想(2)若I′是环R’的理想,则f−1(I′)是环R的理想,且Kerf⊆f−1(I′)
证明不难,可以看书的课后习题 3.4 9
但定理告诉我们,理想在同态满射下是保持的。并且需要指出的是,第二条结论并不需要满射的条件。
商环
同群论中由不变子群引出商群一样,利用理想的概念,我们就可以引出商环的概念了。
设 I I I是环 R R R的一个理想,那么记
R / I = { a + I ∣ a ∈ R } R/I=\{a+I|a\in R\} R/I={a+I∣a∈R}
为 R / I R/I R/I的商集。定义运算为:
( a + I ) + ( b + I ) = ( a + b ) + I ( a + I ) ∗ ( b + I ) = ( a b ) + I (a+I)+(b+I)=(a+b)+I\\ (a+I)*(b+I)=(ab)+I\\ (a+I)+(b+I)=(a+b)+I(a+I)∗(b+I)=(ab)+I
容易验证, R / I R/I R/I关于新定义的乘法和加法做成环,故称它是环 R R R关于理想 I I I的商环。
R / I R/I R/I中的元素也可以称为模 I I I的同余类,这一点可以通过 Z Z Z中 Z / ( n ) Z/(n) Z/(n)来理解
考虑
n
∈
Z
,
(
n
)
=
{
k
n
∣
k
∈
Z
}
n\in Z,(n)=\{kn|k\in Z\}
n∈Z,(n)={kn∣k∈Z}
则
Z
/
(
n
)
=
{
x
+
(
n
)
∣
x
∈
Z
}
=
{
a
+
n
k
∣
k
∈
Z
}
Z/(n)=\{x+(n)|x\in Z\}=\{a+nk|k\in Z\}
Z/(n)={x+(n)∣x∈Z}={a+nk∣k∈Z}
此时
Z
/
(
n
)
Z/(n)
Z/(n)的实际含义是模
n
n
n的剩余类了,即
Z
/
(
n
)
=
{
0
‾
,
1
‾
,
.
.
.
.
n
−
1
‾
}
Z/(n)=\{\overline{0},\overline{1},....\overline{n-1}\}
Z/(n)={0,1,....n−1}
从而模的意义得以体现。
eg:习题3.4 8
环同态基本定理
5.1
环同态基本定理:
设 f : R → R ′ f:R\rightarrow R' f:R→R′是一个环同态映射,则 K e r f = { x ∈ R ∣ f ( x ) = 0 ′ } Kerf=\{x\in R|f(x)=0'\} Kerf={x∈R∣f(x)=0′}是环 R R R的理想,且在 R / K e r f R/Kerf R/Kerf到 R ′ R' R′之间存在唯一的单同态映射满足 f = f ∗ ∘ ϕ f=f_{*}\circ \phi f=f∗∘ϕ,其中 ϕ \phi ϕ为自然同态
f ∗ : R / K e r f → R ′ x + K e r f ↦ f ( x ) f_{*}:R/Kerf\rightarrow R'\\ x+Kerf\mapsto f(x) f∗:R/Kerf→R′x+Kerf↦f(x)
当 f f f为满射的时候, R / K e r f ≅ R ′ R/Kerf\cong R' R/Kerf≅R′
5.2 环同构第一定理


5.3 环同构第二定理

设
R
[
x
]
R[x]
R[x]是实数域
R
\mathbb{R}
R上的多项式环,
I
=
(
x
2
+
1
)
I=(x^2+1)
I=(x2+1),则
R
[
x
]
/
I
≅
C
R[x]/I\cong \Complex
R[x]/I≅C
Proof:
构造
ϕ
:
R
[
x
]
→
C
f
(
x
)
↦
f
(
i
)
\phi:R[x]\rightarrow \Complex\\ f(x)\mapsto f(i)
ϕ:R[x]→Cf(x)↦f(i)
容易证明
ϕ
\phi
ϕ是一个满同态映射从而
R
[
x
]
/
K
e
r
ϕ
→
C
R[x]/Ker\phi \rightarrow \Complex
R[x]/Kerϕ→C
考虑证明
K
e
r
ϕ
=
(
1
+
x
2
)
Ker\phi=(1+x^2)
Kerϕ=(1+x2)
K
e
r
ϕ
=
{
f
(
x
)
∣
f
(
i
)
=
0
}
Ker\phi=\{f(x)|f(i)=0\}
Kerϕ={f(x)∣f(i)=0}
从而
i
i
i是
f
(
x
)
=
0
f(x)=0
f(x)=0的一个根,由于实系数多项式方程的复根是成对出现的,所以
−
i
-i
−i也是该方程的一个根
从而
(
1
+
x
2
)
∣
f
(
x
)
,
∀
f
(
x
)
∈
K
e
r
ϕ
(1+x^2)|f(x),\forall f(x)\in Ker\phi
(1+x2)∣f(x),∀f(x)∈Kerϕ
即
f
(
x
)
=
(
1
+
x
2
)
g
(
x
)
,
g
(
x
)
∈
R
[
x
]
f(x)=(1+x^2)g(x),g(x)\in R[x]
f(x)=(1+x2)g(x),g(x)∈R[x]
从而
K
e
r
ϕ
⊆
(
1
+
x
2
)
Ker\phi\subseteq (1+x^2)
Kerϕ⊆(1+x2)
至于另一个方向,只要把
i
i
i代入即可。从而
K
e
r
ϕ
=
(
1
+
x
2
)
Ker\phi=(1+x^2)
Kerϕ=(1+x2)
□
\square
□
这个东西其实还是有点套路的,比如说,考虑有理数域
Q
\mathbb{Q}
Q上的多项式环
Q
[
x
]
Q[x]
Q[x],我们构造
ϕ
:
Q
[
x
]
→
R
f
(
x
)
↦
f
(
(
2
)
)
\phi:Q[x]\rightarrow R\\ f(x)\mapsto f(\sqrt(2))
ϕ:Q[x]→Rf(x)↦f((2))
容易验证
ϕ
\phi
ϕ是一个环同态(当然它不是满同态,因为
(
3
)
∈
Q
\sqrt(3)\in \mathbb{Q}
(3)∈Q,但它不属于
I
m
g
ϕ
Img\phi
Imgϕ),而
K
e
r
ϕ
=
{
f
(
x
)
∣
f
(
(
2
)
)
=
0
}
Ker\phi=\{ f(x)|f(\sqrt(2))=0 \}
Kerϕ={f(x)∣f((2))=0}
这与上一道题的思路是极其类似的,由于
(
2
)
\sqrt(2)
(2)是方程的一个根,那么
−
(
2
)
-\sqrt(2)
−(2)也是方程的一个根,从而不难证明
K
e
r
ϕ
=
(
x
−
(
(
2
)
)
2
)
=
(
x
−
2
)
Ker\phi=(x-(\sqrt(2))^2)=(x-2)
Kerϕ=(x−((2))2)=(x−2)
素理想与极大理想
素理想
如果
P
P
P是环
R
R
R的一个理想,并且满足
∀
a
,
b
∈
R
,
若
a
b
∈
P
,
则
a
∈
P
,
或
b
∈
P
\forall a,b\in R,若ab\in P,则a\in P,或b\in P
∀a,b∈R,若ab∈P,则a∈P,或b∈P
则
P
P
P是环
R
R
R的一个素理想
对于素理想的判定:
对于一个有单位元的交换环
R
R
R,若
P
P
P是环
R
R
R的一个理想,且
P
≠
R
P\neq R
P=R,则
P
是环
R
的素理想
⇔
R
/
P
是一个整环
P是环R的素理想\Leftrightarrow R/P是一个整环
P是环R的素理想⇔R/P是一个整环
证明略
6.1
从而,我们考虑整数环下的素理想
我们知道,若
P
P
P是整数环
R
R
R的一个素理想,首先有
P
P
P是循环群,从而
P
=
(
m
)
P=(m)
P=(m),于是根据上一判定定理,
Z
/
P
=
Z
/
(
m
)
=
Z
m
是一个整环
⇔
m
是一个素数
Z/P=Z/(m)=Z_m是一个整环\Leftrightarrow m是一个素数
Z/P=Z/(m)=Zm是一个整环⇔m是一个素数
从而,整数环除自身外的所有素理想为
{
(
m
)
∣
m
是素数
}
\{(m)|m是素数\}
{(m)∣m是素数}
我猜这可能也是素理想这个名字的由来?因为整数环中对应的理想都是素数生成的主理想hhh
我们继续考虑如下问题。令
F
F
F是一个域,
F
[
x
]
F[x]
F[x]是
F
F
F上的多项式环,考虑
ϕ
:
F
[
x
]
→
F
f
(
x
)
↦
a
0
\phi:F[x]\rightarrow F\\ f(x)\mapsto a_0
ϕ:F[x]→Ff(x)↦a0
根据环同态的知识,我们不难验证
ϕ
\phi
ϕ是一个环同态满射,从而有
F
[
x
]
/
K
e
r
ϕ
≅
F
F[x]/Ker\phi\cong F
F[x]/Kerϕ≅F
不难验证
K
e
r
ϕ
=
(
x
)
Ker\phi=(x)
Kerϕ=(x)
从而
F
[
x
]
/
(
x
)
≅
F
F[x]/(x)\cong F
F[x]/(x)≅F
这是一个普适结论。更深入的,
F
F
F是一个域,那么它当然是一个整环,于是我们得到
6.2
若 F F F是一个域,F[x]是F上的多项式环,则 ( x ) (x) (x)是 F [ x ] F[x] F[x]的素理想
极大理想
设
M
M
M是环
R
R
R的一个理想,并且
M
≠
R
M\neq R
M=R,若
∀
R
\forall R
∀R的理想N满足
M
⊆
N
⊆
R
M\subseteq N\subseteq R
M⊆N⊆R
都有
N
=
M
N=M
N=M或
N
=
R
N=R
N=R,则称
M
M
M是环
R
R
R的一个极大理想
简单来说,就是 R R R中不存在能完全包含 M M M的真理想
根据定义我们很快就能知道,一个环 R R R可以有多个极大理想,但是事实上并不是每一个环都有极大理想
看看极大理想的判定定理,它与素理想的判定定理是极为类似的
6.3 极大理想的判定定理
对于一个有单位元的交换环 R R R,若 P P P是环 R R R的一个理想,且 P ≠ R P\neq R P=R,则
P 是环 R 的极大理想 ⇔ R / P 是一个域 P是环R的极大理想\Leftrightarrow R/P是一个域 P是环R的极大理想⇔R/P是一个域
证明略
该定理启示我们可以通过极大理想来构造一个域
还是来看看整数环的极大理想长什么样子
若
P
P
P是整数环
R
R
R的一个极大理想,首先有
P
P
P是循环群,从而
P
=
(
m
)
P=(m)
P=(m),于是根据判定定理,
Z
/
P
=
Z
/
(
m
)
=
Z
m
是一个域
⇔
m
是一个素数
Z/P=Z/(m)=Z_m是一个域\Leftrightarrow m是一个素数
Z/P=Z/(m)=Zm是一个域⇔m是一个素数
跟整数环的素理想是同一个集合
{
(
m
)
∣
m
是素数
}
\{(m)|m是素数\}
{(m)∣m是素数},当然这也说明了一个环确实可以有多个极大理想
此外,根据素理想与极大理想的判定定理,两者唯一的区别就是一个的除环是整环,而另一个的除环是域,而显然域一定是一个除环,所以:
6.4
一个有单位元的交换环 R R R的极大理想一定是它的素理想
注意这里的前提是有单位元的交换环
6.5
设 R = 2 Z R=2\mathbb{Z} R=2Z是偶数环, p p p是素数,问 ( 2 p ) (2p) (2p)是否为 R R R的极大理想,是否为 R R R的素理想
R R R是一个无单位元的交换环,所以 ( 2 p ) = { 2 p ∗ 2 k + 2 p ∗ s ∣ k , s ∈ Z } = { 2 k p ∣ k ∈ Z } (2p)=\{2p*2k+2p*s|k,s\in Z\}=\{2kp|k\in Z\} (2p)={2p∗2k+2p∗s∣k,s∈Z}={2kp∣k∈Z}
下面证明 ∀ p \forall p ∀p为素数, ( 2 p ) (2p) (2p)是 2 Z 2\mathbb{Z} 2Z的极大理想
首先显然 ( 2 p ) ≠ 2 Z (2p)\neq 2\mathbb{Z} (2p)=2Z,若有 R R R的理想 M M M,使得 ( 2 p ) ⊆ M ⊆ R (2p)\subseteq M\subseteq R (2p)⊆M⊆R
当
(
2
p
)
⊂
M
(2p)\subset M
(2p)⊂M时,
∃
x
∈
M
,
x
=
2
k
,
x
∉
(
2
p
)
\exist x\in M,x=2k,x\notin (2p)
∃x∈M,x=2k,x∈/(2p),从而
p
p
p不整除
k
k
k,从而
(
x
,
p
)
=
1
(x,p)=1
(x,p)=1,从而
∃
s
,
t
∈
Z
,
x
s
+
p
t
=
1
\exist s,t\in Z,xs+pt=1
∃s,t∈Z,xs+pt=1
则
(
2
x
)
s
+
(
2
p
)
t
=
2
(2x)s+(2p)t=2
(2x)s+(2p)t=2
由于
2
x
,
2
p
∈
M
2x,2p\in M
2x,2p∈M,从而
2
∈
M
2\in M
2∈M.又
M
M
M是循环群
2
Z
2\mathbb{Z}
2Z的理想,所以
M
M
M也是一个循环群,又
2
∈
M
2\in M
2∈M,所以
M
=
(
2
)
=
R
M=(2)=R
M=(2)=R
从而 ( 2 p ) (2p) (2p)是环 R R R的极大理想 (感觉有点难想)
接下来考虑素理想
当 p = 2 p=2 p=2时, ( 2 p ) = ( 4 ) (2p)=(4) (2p)=(4),由 2 ∗ 2 = 4 , 2 ∉ ( 2 p ) 2*2=4,2\notin (2p) 2∗2=4,2∈/(2p)可知, ( 4 ) (4) (4)不是 R R R的素理想
当 p > 2 p>2 p>2时,若 2 k ∗ 2 l ∈ ( 2 p ) , 则 2 p ∣ 4 k l 2k*2l\in (2p),则2p|4kl 2k∗2l∈(2p),则2p∣4kl,从而 p ∣ k p|k p∣k或 p ∣ l p|l p∣l,从而 2 k ∈ ( 2 p ) 2k\in (2p) 2k∈(2p)或 ( 2 l ) ∈ ( 2 p ) (2l)\in (2p) (2l)∈(2p),从而 ( 2 p ) (2p) (2p)是素理想












![达梦数据库报错 执行失败(语句1) -2111: 第1 行附近出现错误: 无效的列名[system]](https://img-blog.csdnimg.cn/direct/ac26cb0770b34e6980b8e6e131c202c1.png)