背景:网上很多关于矩阵乘的编程优化思路,本着看理论分析万遍,不如实际代码写一遍的想法,大概过一下优化思路。
矩阵乘的定义如下,约定矩阵的形状及存储方式为: A[M, K], B[K, N], C[M, N]。
CPU篇
朴素实现方法
按照常规的思路,实现矩阵乘时如下的3层for循环。
#define OFFSET(row, col, ld) ((row) * (ld) + (col))
void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K)
{
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n++) {
float psum = 0.0;
for (int k = 0; k < K; k++) {
psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
}
c[OFFSET(m, n, N)] = psum;
}
}
}数据访存连续的优化
矩阵B的存储默认为N方向连续,所以可以将上面的第2,3层循环互换顺序,这样B的取数就不会跨行了,而是连续取数,达到访问连续的效果。
void cpuSgemm_1(float *a, float *b, float *c, const int M, const int N, const int K)
{
for (int m = 0; m < M; m++) {
for (int k = 0; k < K; k++) {
for (int n = 0; n < N; n++)
{
c[OFFSET(m, n, N)] += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
}
}
}
}数据重排/数据复用的优化
上面将M,N,K的for循环调整为M,K,N的循环顺序,导致我们K方向累加不能缓存了,增加了多次访问C矩阵的开销,所以我们不放先直接将B矩阵转置处理,然后再按照原始的M,N,K的for循环来处理。
void cpuSgemm_2(float *a, float *b, float *c, const int M, const int N, const int K)
{
float* b1=(float*) malloc(sizeof(float)*K*N);
for(int i=0; i<K; i++)
{
for (int j=0; j<N; j++)
{
b1[OFFSET(j,i,K)]= b[OFFSET(i,j,N)];
}
}
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n++) {
float psum = 0.0;
for (int k = 0; k < K; k++) {
psum += a[OFFSET(m, k, K)] * b1[OFFSET(n, k, K)];
}
c[OFFSET(m, n, N)] = psum;
}
}
}性能表现
如下是测试CPU环境下这几种方法的时间情况,其中M=N=512, K =256。可以发现经过优化后的代码在时间上是逐步减少的。
CPU的优化思路还有其他的,比如循环展开,intrinsic函数,基于cache的矩阵切分等,注意本文并没有都实现出来。
cpuSgemm, Time measured: 416889 microseconds.
cpuSgemm_1, Time measured: 405259 microseconds.
cpuSgemm_2, Time measured: 238786 microseconds.GPU篇
grid线程循环矩阵乘法
输出矩阵C有M*N个点,每个点是K个数的乘积和,所以可以定义每个线程计算K个点的乘积和,即grid线程循环矩阵乘法。
__global__ void matrix_multiply_gpu_0(float*a, float*b, float*c, int M, int N, int K)
{
int tidx =threadIdx.x;
int bidx = blockIdx.x;
int idx = bidx * blockDim.x +tidx;
int row = idx/N;
int col = idx%N;
if(row<M && col < N)
{
float tmp =0.0;
for(int k=0; k<K; k++)
{
tmp+=a[row*K+k] * b[k*N+col];
}
c[row*N+col] = tmp;
}
}block线程循环矩阵乘法
grid内线程循环的矩阵乘法有如下缺憾:一个block内线程可能需要计算C矩阵不同行的矩阵元素,block内thread对相应的A矩阵访存不一致,导致无法广播和额外的访存开销,导致执行时间增加。
针对这个问题,可以做如下改进:每个block计算C矩阵的一行,block内的thread以固定跳步步长blockDim.x的方法循环计算C矩阵的一行,每一行启动一个block,共计M个block。
__global__ void matrix_multiply_gpu_1(float*a, float*b, float*c, int M, int N, int K)
{
int tidx =threadIdx.x;
int bidx = blockIdx.x;
float tmp;
for(;bidx<M; bidx += gridDim.x)
{
for(;tidx<N; tidx+=blockDim.x )
{
tmp=0.0;
for(int k=0; k<K; k++)
{
tmp+=a[bidx*K +k] * b[k*N+tidx];
}
c[bidx*N+tidx] = tmp;
}
}
}
行共享存储矩阵乘法
共享存储与L1 Cache同级,其访存延迟较全局存储小一个量级。用共享存储代替全局存储是GPU最重要的优化手段之一。采用共享存储优化的关键是数据复用,数据复用次数越多,共享存储优化可获得的收益也越高。
在block循环乘法中,1个block内所有thread都会用到A矩阵的一行,此时与B矩阵每一列相乘,A矩阵中该行复用了N次。故可以考虑将A矩阵的一行读入shared memory,运算时候从shared memory读取相应的数据。
注意代码中TILE_WIDTH>=K。
#define TILE_WIDTH 256
__global__ void matrix_multiply_gpu_2(float*a, float*b, float*c, int M, int N, const int K)
{
__shared__ float data[TILE_WIDTH];
int tid = threadIdx.x;
int row = blockIdx.x;
int i,j;
for(i=tid; i<K; i+=blockDim.x)
{
data[i]=a[row*K +i];
}
__syncthreads();
float tmp;
for(j=tid; j<N; j+=blockDim.x)
{
tmp=0.0;
for(int k=0; k<K; k++)
{
tmp += data[k]*b[k*N+j];
}
c[row*N+j] = tmp;
}
}
分块共享存储矩阵乘法
根据上面共享存储的理解,我们很自然的想到把B矩阵也考虑数据复用,所以可以同时把A,B矩阵都分成棋盘似的小尺寸的数据块,从全局内存读取到共享内存,这样可以有效降低数据访问时间,充分复用矩阵乘的局部数据。
#define TILE_SIZE 32
__global__ void matrix_multiply_gpu_3(float*a, float*b, float*c, int M, int N, const int K)
{
__shared__ float matA[TILE_SIZE][TILE_SIZE];
__shared__ float matB[TILE_SIZE][TILE_SIZE];
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
int Col = bx * TILE_SIZE + tx;
int Row = by * TILE_SIZE + ty;
float Pervalue = 0.0;
for(int i = 0;i < K / TILE_SIZE;i++)
{
matA[ty][tx] = a[Row * K + (i * TILE_SIZE + tx)];
matB[ty][tx] = b[Col + (i * TILE_SIZE + ty) * N];
__syncthreads();
for(int k = 0;k < TILE_SIZE;k++)
Pervalue += matA[ty][k] * matB[k][tx];
__syncthreads();
}
c[Row * N + Col] = Pervalue;
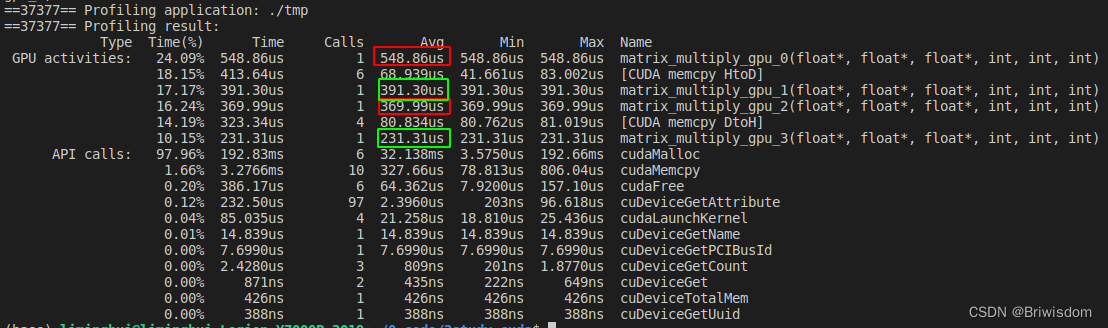
}性能表现
利用nvprof工具,统计各个核函数的执行时间如下,可以发现每一步优化思路都能直观的带来的性能提升。
完整代码:
GitHub - Briwisdom/study_CUDA_examples: some demos for study CUDA program.
#include <iostream>
#include <chrono>
using namespace std;
#define OFFSET(row, col, ld) ((row) * (ld) + (col))
void initDate(float *arr,int Len, bool randFlag=true)
{
if (randFlag)
{
for (int i = 0; i < Len; i++) {
arr[i] = rand()/1000000;
}
}
else
{
float value =0.0;
for (int i = 0; i < Len; i++) {
arr[i] = value;
}
}
}
void compare_result(float *x, float *y, int n, char *name)
{
int cnt=0;
for (int i=0; i<n; i++)
{
if (x[i]!=y[i])
{
cnt++;
printf("x= %f, y= %f\n", x[i],y[i]);
}
}
printf("%s, ", name);
if(cnt ==0)
printf("result matched.\n");
else
printf("something error! result not match number = %d int total number: %d .\n", cnt, n);
}
void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K)
{
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n++) {
float psum = 0.0;
for (int k = 0; k < K; k++) {
psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
}
c[OFFSET(m, n, N)] = psum;
}
}
}
void cpuSgemm_1(float *a, float *b, float *c, const int M, const int N, const int K)
{
for (int m = 0; m < M; m++) {
for (int k = 0; k < K; k++) {
for (int n = 0; n < N; n++)
{
c[OFFSET(m, n, N)] += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];
}
}
}
}
void cpuSgemm_2(float *a, float *b, float *c, const int M, const int N, const int K)
{
float* b1=(float*) malloc(sizeof(float)*K*N);
for(int i=0; i<K; i++)
{
for (int j=0; j<N; j++)
{
b1[OFFSET(j,i,K)]= b[OFFSET(i,j,N)];
}
}
for (int m = 0; m < M; m++) {
for (int n = 0; n < N; n++) {
float psum = 0.0;
for (int k = 0; k < K; k++) {
psum += a[OFFSET(m, k, K)] * b1[OFFSET(n, k, K)];
}
c[OFFSET(m, n, N)] = psum;
}
}
}
void operation(void (*func)(float*,float*, float*, int, int, int), float *a, float *b, float *c, const int M, const int N, const int K, int repeat, char* name)
{
auto begin0 = std::chrono::high_resolution_clock::now();
for(int i=0; i<repeat; i++)
{
(*func)(a,b,c, M, N, K);
}
auto end0 = std::chrono::high_resolution_clock::now();
auto elapsed0 = std::chrono::duration_cast<std::chrono::microseconds>(end0 - begin0);
printf("%s, Time measured: %d microseconds.\n", name, int(elapsed0.count()/repeat));
}
__global__ void matrix_multiply_gpu_0(float*a, float*b, float*c, int M, int N, int K)
{
int tidx =threadIdx.x;
int bidx = blockIdx.x;
int idx = bidx * blockDim.x +tidx;
int row = idx/N;
int col = idx%N;
if(row<M && col < N)
{
float tmp =0.0;
for(int k=0; k<K; k++)
{
tmp+=a[row*K+k] * b[k*N+col];
}
c[row*N+col] = tmp;
}
}
__global__ void matrix_multiply_gpu_1(float*a, float*b, float*c, int M, int N, int K)
{
int tidx =threadIdx.x;
int bidx = blockIdx.x;
float tmp;
for(;bidx<M; bidx += gridDim.x)
{
for(;tidx<N; tidx+=blockDim.x )
{
tmp=0.0;
for(int k=0; k<K; k++)
{
tmp+=a[bidx*K +k] * b[k*N+tidx];
}
c[bidx*N+tidx] = tmp;
}
}
}
#define TILE_WIDTH 256
__global__ void matrix_multiply_gpu_2(float*a, float*b, float*c, int M, int N, const int K)
{
__shared__ float data[TILE_WIDTH];
int tid = threadIdx.x;
int row = blockIdx.x;
int i,j;
for(i=tid; i<K; i+=blockDim.x)
{
data[i]=a[row*K +i];
}
__syncthreads();
float tmp;
for(j=tid; j<N; j+=blockDim.x)
{
tmp=0.0;
for(int k=0; k<K; k++)
{
tmp += data[k]*b[k*N+j];
}
c[row*N+j] = tmp;
}
}
#define TILE_SIZE 32
__global__ void matrix_multiply_gpu_3(float*a, float*b, float*c, int M, int N, const int K)
{
__shared__ float matA[TILE_SIZE][TILE_SIZE];
__shared__ float matB[TILE_SIZE][TILE_SIZE];
int bx = blockIdx.x;
int by = blockIdx.y;
int tx = threadIdx.x;
int ty = threadIdx.y;
int Col = bx * TILE_SIZE + tx;
int Row = by * TILE_SIZE + ty;
float Pervalue = 0.0;
for(int i = 0;i < K / TILE_SIZE;i++)
{
matA[ty][tx] = a[Row * K + (i * TILE_SIZE + tx)];
matB[ty][tx] = b[Col + (i * TILE_SIZE + ty) * N];
__syncthreads();
for(int k = 0;k < TILE_SIZE;k++)
Pervalue += matA[ty][k] * matB[k][tx];
__syncthreads();
}
c[Row * N + Col] = Pervalue;
}
int main()
{
int M=512;
int N=512;
int K=256;
float *a = (float*) malloc(M*K * sizeof(float));
float *b = (float*) malloc(N*K * sizeof(float));
float *c = (float*) malloc(M*N * sizeof(float));
float *c1 = (float*) malloc(M*N * sizeof(float));
float *c2 = (float*) malloc(M*N * sizeof(float));
float *c_gpu_0 = (float*) malloc(M*N * sizeof(float));
float *c_gpu_1 = (float*) malloc(M*N * sizeof(float));
float *c_gpu_2 = (float*) malloc(M*N * sizeof(float));
float *c_gpu_3 = (float*) malloc(M*N * sizeof(float));
initDate(a,M*K);
initDate(b,N*K);
initDate(c, M*N, false);
initDate(c1, M*N, false);
initDate(c2, M*N, false);
initDate(c_gpu_0, M*N, false);
initDate(c_gpu_1, M*N, false);
initDate(c_gpu_2, M*N, false);
initDate(c_gpu_3, M*N, false);
//ensure result is right.
cpuSgemm(a,b,c,M,N,K);
cpuSgemm_1(a,b,c1,M,N,K);
cpuSgemm_2(a,b,c2,M,N,K);
compare_result(c, c1, M*N,"sgemm1");
compare_result(c, c2, M*N,"sgemm2");
//test the prerformance.
int repeat =10;
operation(cpuSgemm,a,b,c,M,N,K,repeat,"cpuSgemm");
operation(cpuSgemm_1,a,b,c1,M,N,K,repeat,"cpuSgemm_1");
operation(cpuSgemm_2,a,b,c2,M,N,K,repeat,"cpuSgemm_2");
float* d_a, *d_b, *d_c0, *d_c1, *d_c2, *d_c3;
cudaMalloc((void**) &d_a, sizeof(float)*(M*K));
cudaMalloc((void**) &d_b, sizeof(float)*(N*K));
cudaMalloc((void**) &d_c0, sizeof(float)*(M*N));
cudaMalloc((void**) &d_c1, sizeof(float)*(M*N));
cudaMalloc((void**) &d_c2, sizeof(float)*(M*N));
cudaMalloc((void**) &d_c3, sizeof(float)*(M*N));
cudaMemcpy(d_a, a, sizeof(float)*M*K, cudaMemcpyHostToDevice);
cudaMemcpy(d_b, b, sizeof(float)*N*K, cudaMemcpyHostToDevice);
int threadnum=64;
int blocks =(M*N+threadnum-1)/threadnum;
cudaMemcpy(d_c0, c_gpu_0, sizeof(float)*M*N, cudaMemcpyHostToDevice);
matrix_multiply_gpu_0<<<blocks, threadnum>>>(d_a, d_b, d_c0, M, N, K);
cudaMemcpy(c_gpu_0, d_c0, sizeof(float)*M*N, cudaMemcpyDeviceToHost);
compare_result(c, c_gpu_0, M*N,"gpu_0");
cudaFree(d_c0);
cudaMemcpy(d_c1, c_gpu_1, sizeof(float)*M*N, cudaMemcpyHostToDevice);
matrix_multiply_gpu_1<<<M, threadnum>>>(d_a, d_b, d_c1, M, N, K);
cudaMemcpy(c_gpu_1, d_c1, sizeof(float)*M*N, cudaMemcpyDeviceToHost);
compare_result(c, c_gpu_1, M*N,"gpu_1");
cudaFree(d_c1);
cudaMemcpy(d_c2, c_gpu_2, sizeof(float)*M*N, cudaMemcpyHostToDevice);
matrix_multiply_gpu_2<<<M, threadnum>>>(d_a, d_b, d_c2, M, N, K);
cudaMemcpy(c_gpu_2, d_c2, sizeof(float)*M*N, cudaMemcpyDeviceToHost);
compare_result(c, c_gpu_2, M*N,"gpu_2");
cudaFree(d_c2);
threadnum=32;
dim3 gridSize(M / threadnum,N / threadnum);
dim3 blockSize(threadnum,threadnum);
cudaMemcpy(d_c3, c_gpu_3, sizeof(float)*M*N, cudaMemcpyHostToDevice);
matrix_multiply_gpu_3<<<gridSize, blockSize>>>(d_a, d_b, d_c3, M, N, K);
cudaMemcpy(c_gpu_3, d_c3, sizeof(float)*M*N, cudaMemcpyDeviceToHost);
compare_result(c, c_gpu_3, M*N,"gpu_3");
cudaFree(d_c3);
free(a);
free(b);
free(c);
free(c1);
free(c2);
free(c_gpu_0);
free(c_gpu_1);
free(c_gpu_2);
free(c_gpu_3);
cudaFree(d_a);
cudaFree(d_b);
}