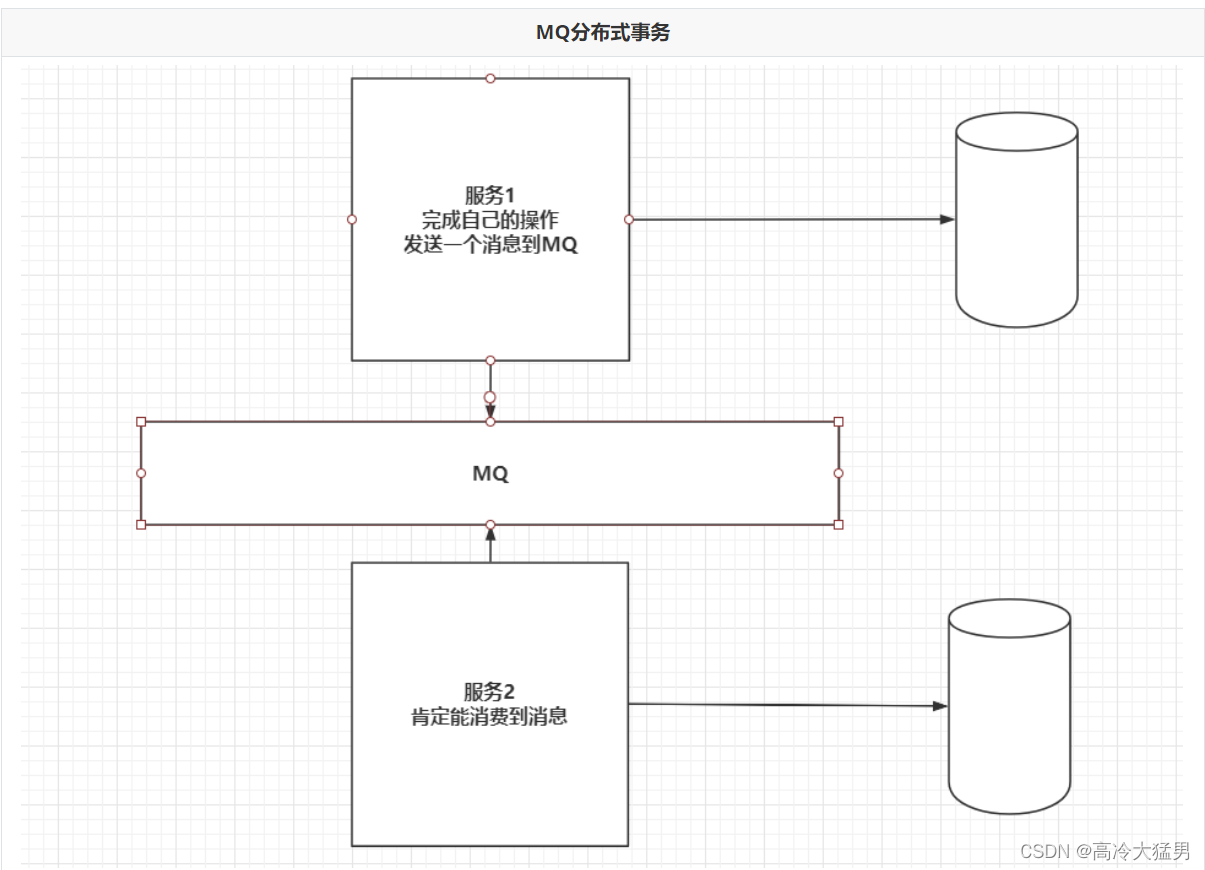
统计学中的Bootstrap方法（Bootstrap抽样）用来训练bagging算法，如果随机森林Random Forests

提示：系列被面试官问的问题，我自己当时不会，所以下来自己复盘一下，认真学习和总结，以应对未来更多的可能性

关于互联网大厂的笔试面试，都是需要细心准备的
（1）自己的科研经历，科研内容，学习的相关领域知识，要熟悉熟透了
（2）自己的实习经历，做了什么内容，学习的领域知识，要熟悉熟透了
（3）除了科研，实习之外，平时自己关注的前沿知识，也不要落下，仔细了解，面试官很在乎你是否喜欢追进新科技，跟进创新概念和技术
（4）准备数据结构与算法，有笔试的大厂，第一关就是手撕代码做算法题
面试中，实际上，你准备数据结构与算法时以备不时之需，有足够的信心面对面试官可能问的算法题，很多情况下你的科研经历和实习经历足够跟面试官聊了，就不需要考你算法了。但很多大厂就会面试问你算法题，因此不论为了笔试面试，数据结构与算法必须熟悉熟透了
秋招提前批好多大厂不考笔试，直接面试，能否免笔试去面试，那就看你简历实力有多强了。

---

文章目录

• 统计学中的Bootstrap方法（Bootstrap抽样）用来训练bagging算法，如果随机森林Random Forests
• • @[TOC](文章目录)
• 统计学中的Bootstrap方法（Bootstrap抽样）
• 训练bagging算法：随机森林Random Forests
• 总结

统计学中的Bootstrap方法（Bootstrap抽样）

有放回的采样方法叫bootstrip采样方法

为啥它很好呢
举个例子

Bootstrap又称自展法、自举法、自助法、靴带法 , 是统计学习中一种重采样(Resampling)技术，用来估计标准误差、置信区间和偏差

子样本之于样本，可以类比样本之于总体

举例
栗子：我要统计鱼塘里面的鱼的条数，怎么统计呢？
假设鱼塘总共有鱼N，不知道N是多少条

步骤：

1. 承包鱼塘，不让别人捞鱼(规定总体分布不变)。
2. 自己捞鱼，捞100条，都打上标签(构造样本)
3. 把鱼放回鱼塘，休息一晚(使之混入整个鱼群，确保之后抽样随机)
4. 开始捞鱼，每次捞100条，数一下，自己昨天标记的鱼有多少条，占比多少(一次重采样取分布)。
5. 然后把这100条又放回去
6. 重复3，4步骤n次。建立分布。

（原理是中心极限定理）

假设一下，第一次重新捕鱼100条，发现里面有标记的鱼12条，记下为12%，
放回去，再捕鱼100条，发现标记的为9条，记下9%，
重复重复好多次之后，假设取置信区间95%，
你会发现，每次捕鱼平均在10条左右有标记，

它怎么来的呢？
10/N=10%

所以，我们可以大致推测出鱼塘有1000条左右。

其实是一个很简单的类似于一个比例问题。这也是因为提出者Efron给统计学顶级期刊投稿的时候被拒绝的理由–“太简单”。这也就解释了，为什么在小样本的时候，bootstrap效果较好，

你这样想，如果我想统计大海里有多少鱼，你标记100000条也没用啊，因为实际数量太过庞大，
你取的样本相比于太过渺小，最实际的就是，你下次再捕100000的时候，发现一条都没有标记，就尴尬了。。。

————————————————
版权声明：本文为CSDN博主「hxxjxw」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/hxxjxw/article/details/108265491

---

训练bagging算法：随机森林Random Forests

Bootstrap是现代统计学较为流行的一种统计方法，在小样本时效果很好。机器学习中的Bagging，AdaBoost等方法其实都蕴含了Boostrap的思想，在集成学习的范畴里 Bootstrap直接派生出了Bagging模型.

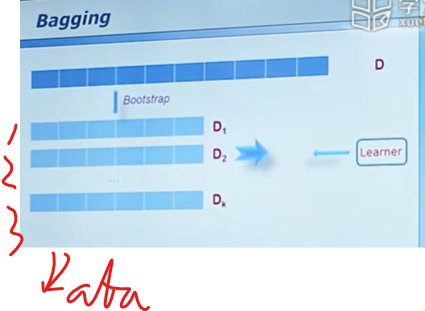
不妨设分类是2分类问题
怎么集合？

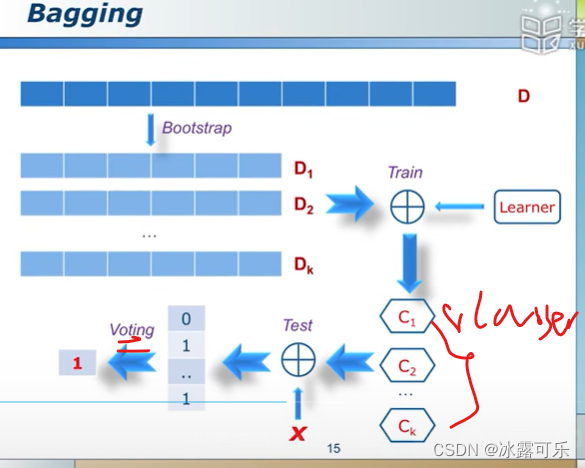
不妨设异或来voting

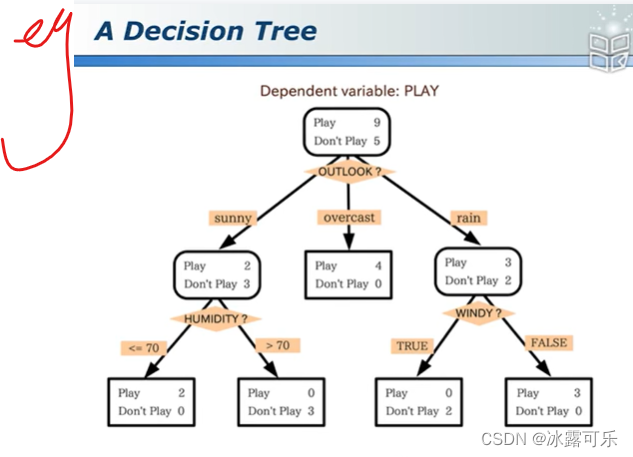
这是一个分类的决策树

如果有很多这种树
组合成随机森林RF

一般来说2/3的数据都会被选中

那就看多数决策树，他们分类是啥，咱就以多数投票为准

树们有多样性，保证个案分类都很骚

有1/3的样本没有被选中的，拿来做交叉验证集，美滋滋

虽然不同的小树，他们可以过拟合
但整体来说，它就是一个特征区分的小模块，美滋滋
整体OK就行的

---

总结

提示：重要经验：

1）
2）
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。