1）二维矩阵代码

clear all
clc

% 定义目标函数
fun = @(x) sum(sum(x.^2));

% 初始矩阵
x0 = 2 + rand(2, 2);

% 定义空的线性不等式约束
A = [];
b = [];

% 定义空的线性等式约束
Aeq = [];
beq = [];

% 定义变量的上下界
lb = ones(2,2);
ub = [];

% 使用 fmincon 求解
options = optimoptions('fmincon', 'Display', 'iter');
[x_opt, fval_opt] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, [], options);

% 显示最优解和最优值
disp('最优解：');
disp(x_opt);
disp('最优值：');
disp(fval_opt);

2）运行结果

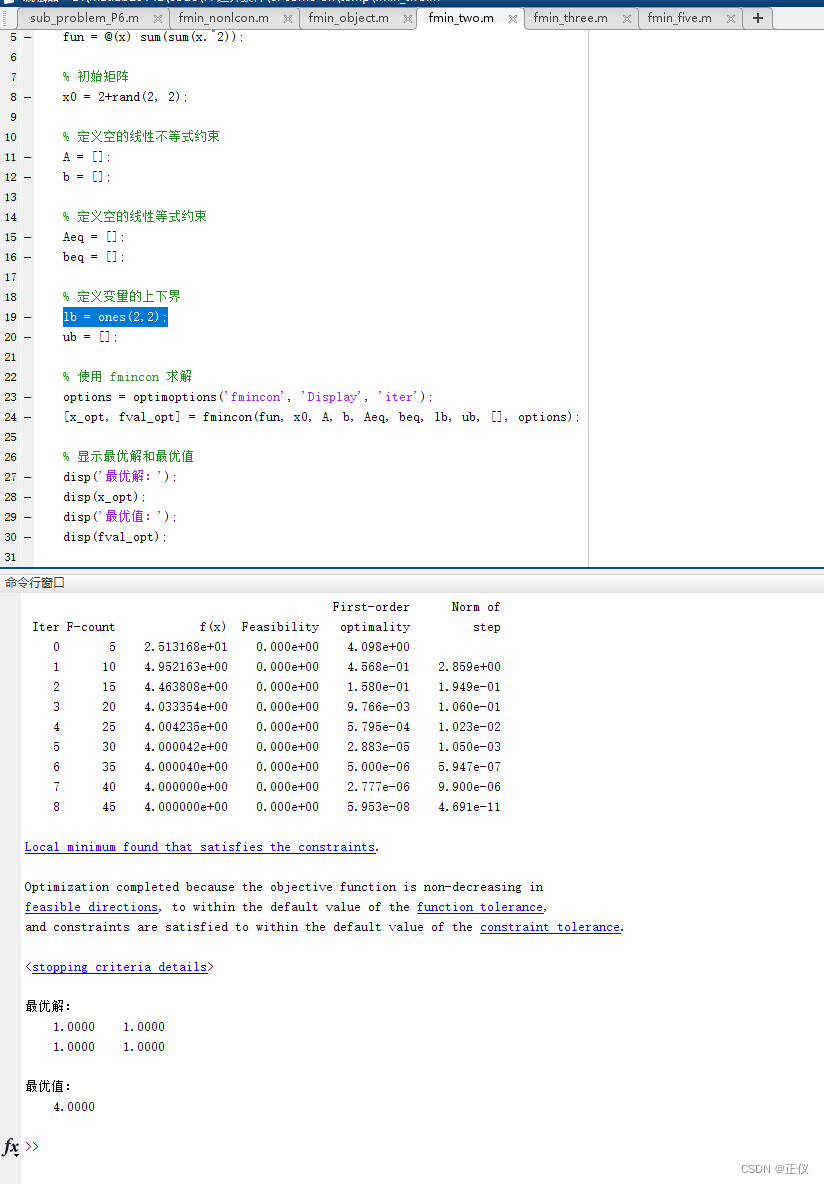
由此可见，确实可计算得到最优解！.

3）高维矩阵代码（五维）

clear all
clc

% 定义目标函数
fun = @(x) sum(sum(sum(sum(sum(x.^2)))));

% 初始矩阵（五维）
x0 = 2 + rand(2, 2, 2, 2, 2);

% 定义空的线性不等式约束
A = [];
b = [];

% 定义空的线性等式约束
Aeq = [];
beq = [];

% 定义变量的上下界
lb = ones(2, 2, 2, 2, 2);
ub = [];

% 使用 fmincon 求解
options = optimoptions('fmincon', 'Display', 'iter');
[x_opt, fval_opt] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, [], options);

% 显示最优解和最优值
disp('最优解：');
disp(x_opt);
disp('最优值：');
disp(fval_opt);

4）运行结果

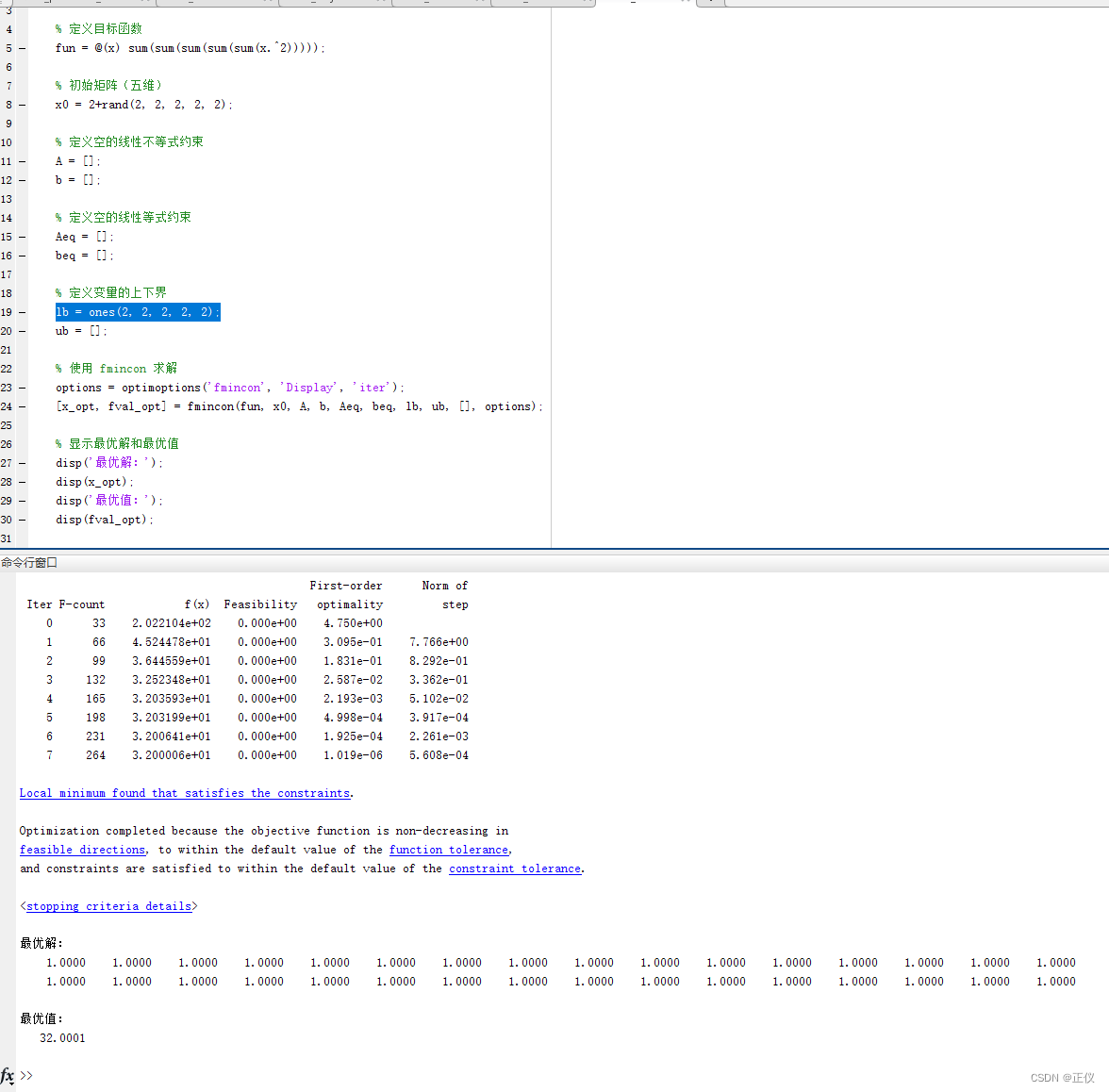
此外，即使是凸优化问题，fmin仍可能会显示求得“Local minimum found that satisfies the constraints.”

5）需要注意：非常不建议fmin中使用高维矩阵（三维及三维以上）

因为，第一轮迭代时，“决策变量”是初始的高维矩阵（434维矩阵）；但在第二轮迭代时，目标函数中的“决策变量”、以及非线性约束中的“决策变量”，就全部变为二维矩阵了！（因为第一轮迭代的结果，会以二维矩阵的形式来存储！所以，在第二轮迭代时，决策变量又变成了4*12维的二维矩阵！）

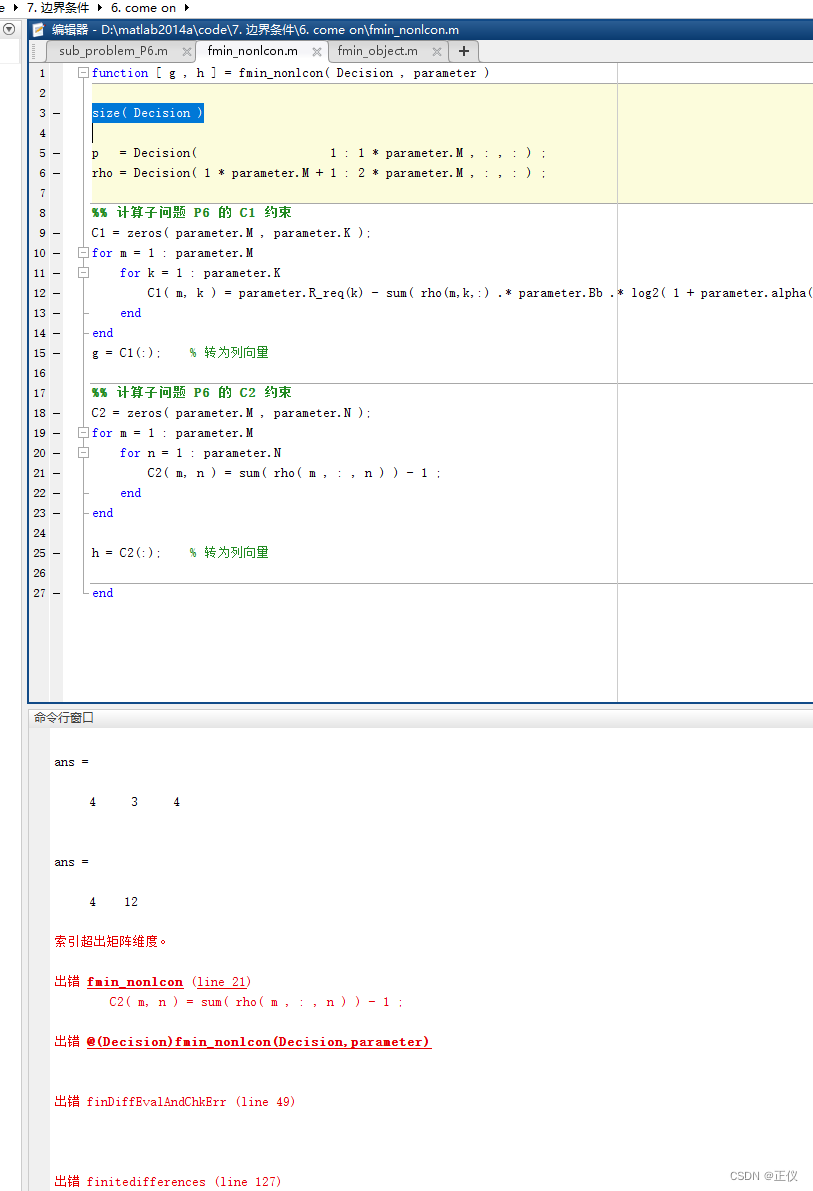
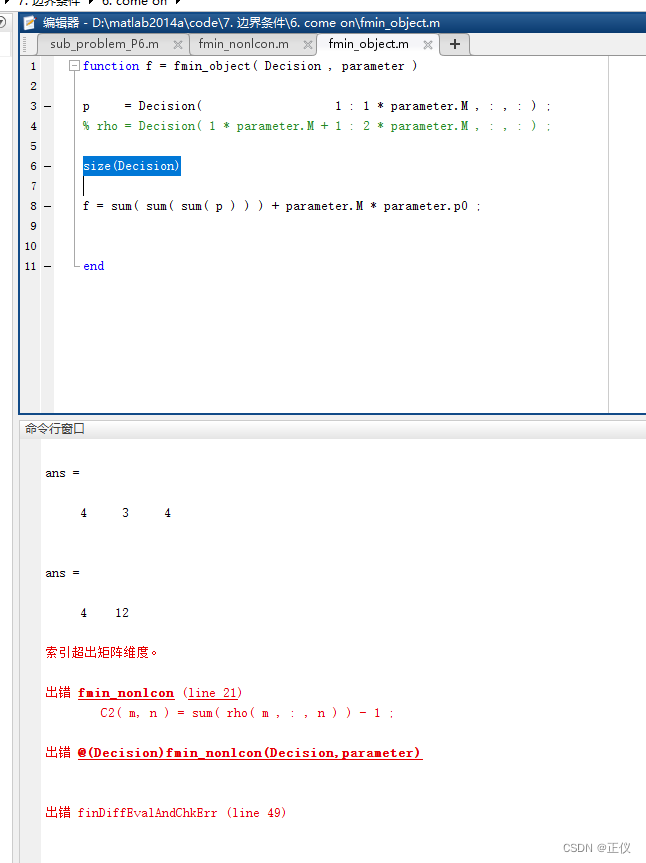
因此，建议fmin中的决策变量，最高维度只设为二维矩阵！！不建议设成高维矩阵！！