文章目录
- 一、LR分析法
- 1、概念
- 2、流程
- 3、LR分析器结构及分析表构造
- 1)结构
- 2)一些概念
- 二、LR(0)分析法
- 1、流程
- 2、分析动作
- 1)移近
- 2)归约(reduce)
- 3、总结
- 1)LR分析器
- 2)构造DFA
- 3)构造LR(0)的方法(三步)
- 4、局限性
- 三、LR(1)分析法
- 四、SLR(1):简单LR分析法
- 1、基本思想
- 2、分析思路
- 1)构建表
- 2)SLR求ACTION表
- 3、局限性
- 五、彩蛋
一、LR分析法
1、概念
是一种自底向上的分析方法(1965年 D.Knuth 提出)。
L:从左向右分析 (left to right)
R:产生“最右推导”(right-most derivation)
k=0:不向前查看符号 k=1:向前查看1个符号
从左到右扫描(L)自底向上进行归约(Right-most Derivation)(一定是规范归约), 是自底向上分析方法的高度概括和集中
历史 + 展望 + 现状 => 句柄
2、流程
根据文法不断进行移进或者规约
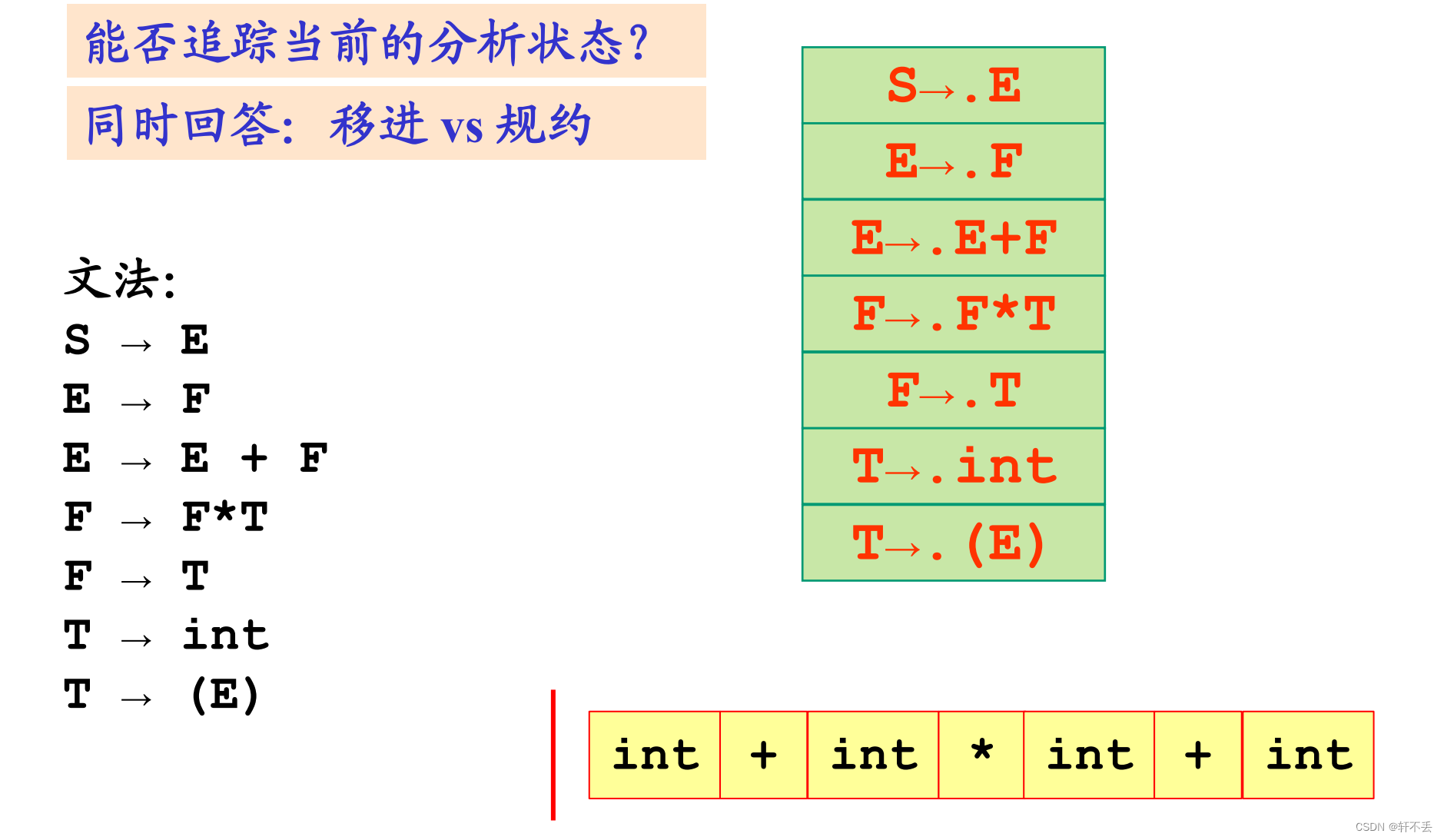
规约后回退状态,且得到的终结符也需要回退
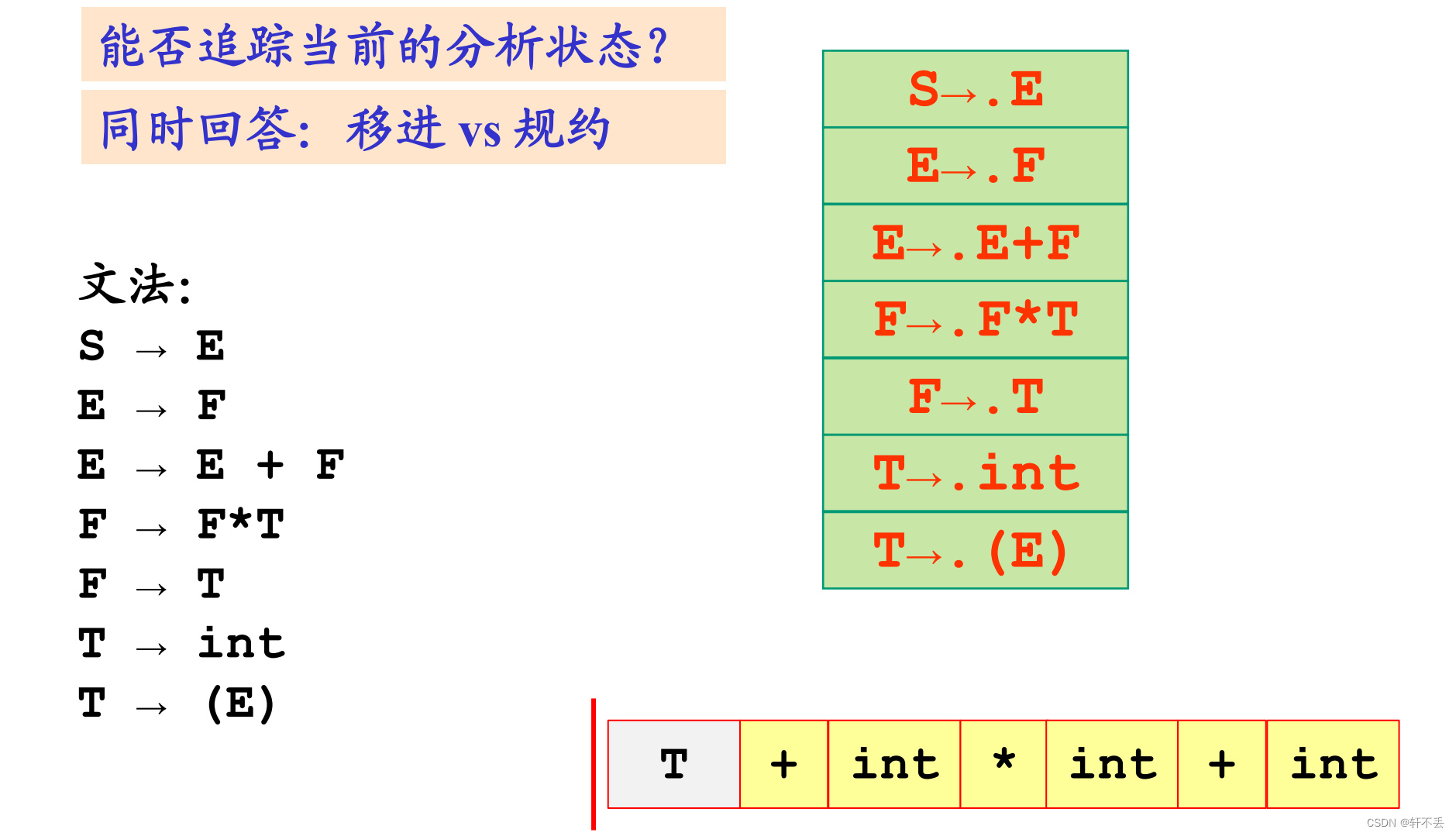
3、LR分析器结构及分析表构造
1)结构
状态栈、分析表、控制程序
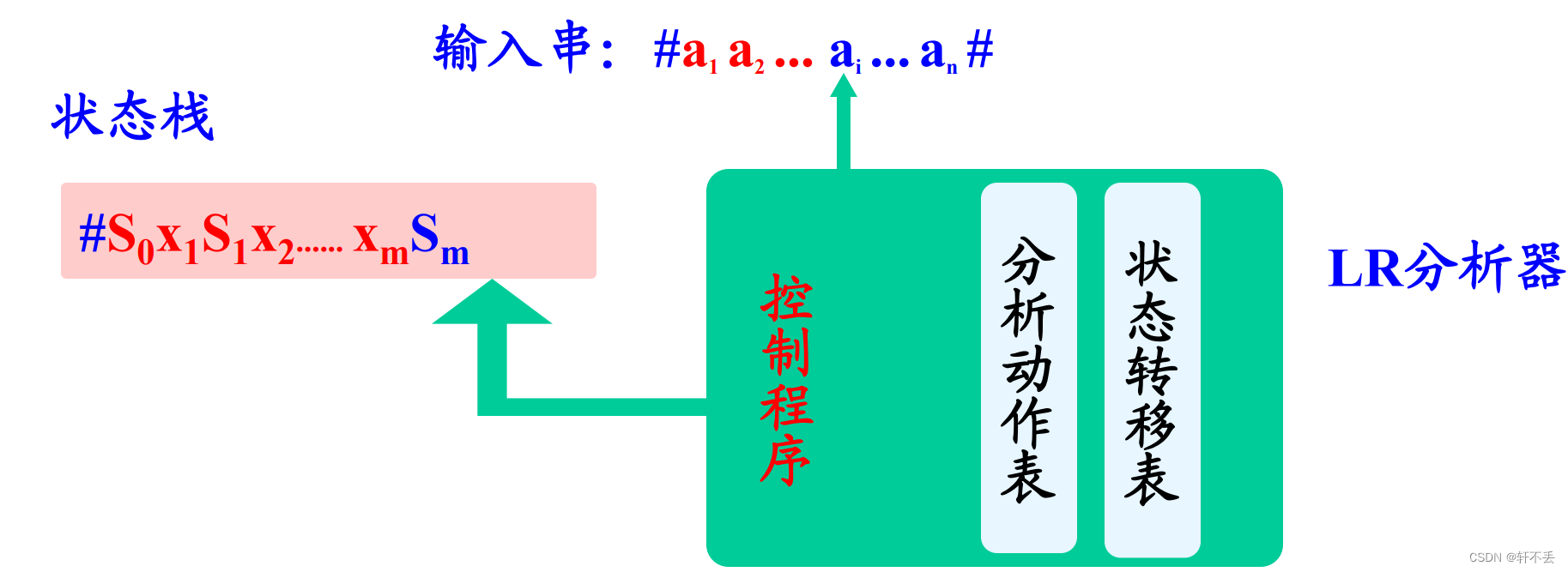
栈顶状态概括了从分析开始到该状态的全部分析历史和展望信息
2)一些概念
符号串 X 1 X 2 . . . . . X m X_1X_2..... X_m X1X2.....Xm:从开始状态( S 0 S_0 S0)到当前状态( S m S_m Sm)所识别的规范句型的活前缀。
规范句型前缀: 将输入串的剩余部分与其连接起来就构成了规范句型。
如:
x
1
x
2
.
.
.
.
.
x
m
a
i
.
.
.
a
n
x_1x_2..... x_ma_i... a_n
x1x2.....xmai...an为规范句型(
x
i
x_i
xi已处理,
a
i
a_i
ai未处理)
对于句型
α
β
t
αβt
αβt,
β
β
β表示句柄, 如果
α
β
=
u
1
u
2
…
u
r
αβ= u_1u_2…u_r
αβ=u1u2…ur那么符号串
u
1
u
2
…
u
i
(
1
≤
i
≤
r
)
u_1u_2…u_i(1≤i≤r)
u1u2…ui(1≤i≤r)即是句型
α
β
t
αβt
αβt的活前缀。
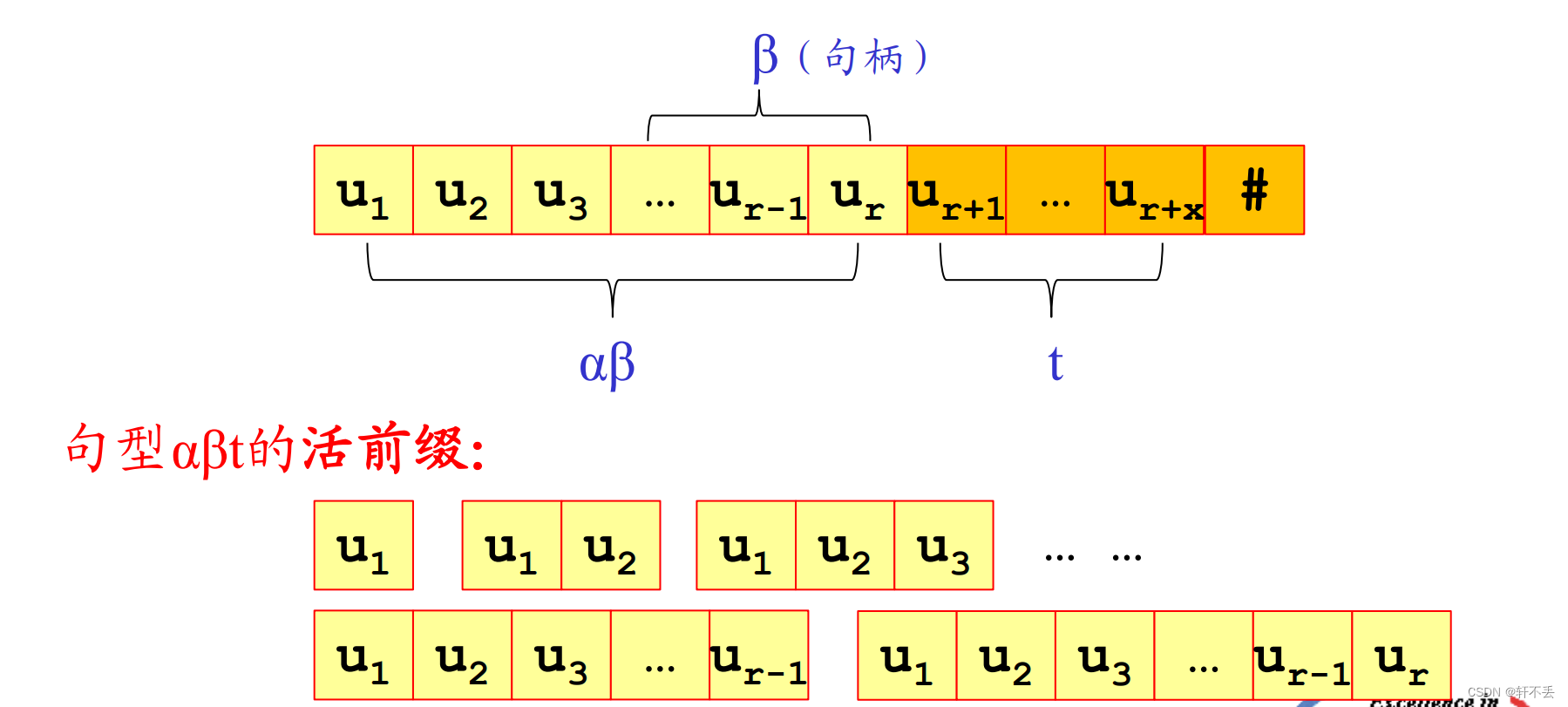
活前缀: 若分析过程能够保证栈中符号串均是规范句型的前缀,则表示输入串已分析过的部分没有语法错误,所以称为规范句型的活前缀。
二、LR(0)分析法
1、流程
根据状态转移图得出状态转移表
状态栈:#
S
0
x
1
S
1
x
2
.
.
.
.
.
.
x
i
−
1
S
i
−
1
x
i
S
i
S_0x_1S_1x_2...... x_{i-1}S_{i-1} x_iS_i
S0x1S1x2......xi−1Si−1xiSi
S
i
−
1
S_{i-1}
Si−1—当前状态(栈顶状态)
x
i
x_i
xi— 新的栈顶符号
S
i
S_i
Si----新的栈顶状态(状态转移)
2、分析动作
1)移近
A
C
T
I
O
N
[
S
i
,
a
]
=
s
ACTION[S_i,a] = s
ACTION[Si,a]=s (s表示
s
h
i
f
t
shift
shift,移进)
动作: 将
a
a
a推进栈,并设置新的栈顶状态
S
j
S_j
Sj
S
j
=
G
O
T
O
[
S
i
,
a
]
S_j= GOTO[S_i,a]
Sj=GOTO[Si,a],将指针指向下一个输入符号
2)归约(reduce)
A
C
T
I
O
N
[
S
i
,
a
]
=
r
d
ACTION [S_i,a] = r_d
ACTION[Si,a]=rd (r表示 reduce,按规则d规约)
条件:某个项目集形如
A
→
β
A→β
A→β.
动作: 将符号串β(假定长度为
n
n
n)连同状态从栈内
弹出, 把
A
A
A推进栈, 并设置新的栈顶状态
S
j
S_j
Sj
S
j
=
G
O
T
O
[
S
i
−
n
,
A
]
S_j= GOTO[S_{i-n},A]
Sj=GOTO[Si−n,A]
3、总结
1)LR分析器
构造LR分析器的关键是构造其分析表
构造LR分析表的方法是:
- 根据文法构造识别规范句型活前缀的有穷自动机DFA
- 由DFA构造分析表
2)构造DFA

构造DFA:
4. 确定
S
S
S集合,即
L
R
(
0
)
LR(0)
LR(0)项目集规范族,同时确定
S
0
S_0
S0
5. 确定状态转移函数GOTO
LR(0) 是DFA的状态集,其中每个状态又都是项目的集合
项目:文法G的每个产生式(规则)的右部添加一个圆点就构成一个项目

3)构造LR(0)的方法(三步)
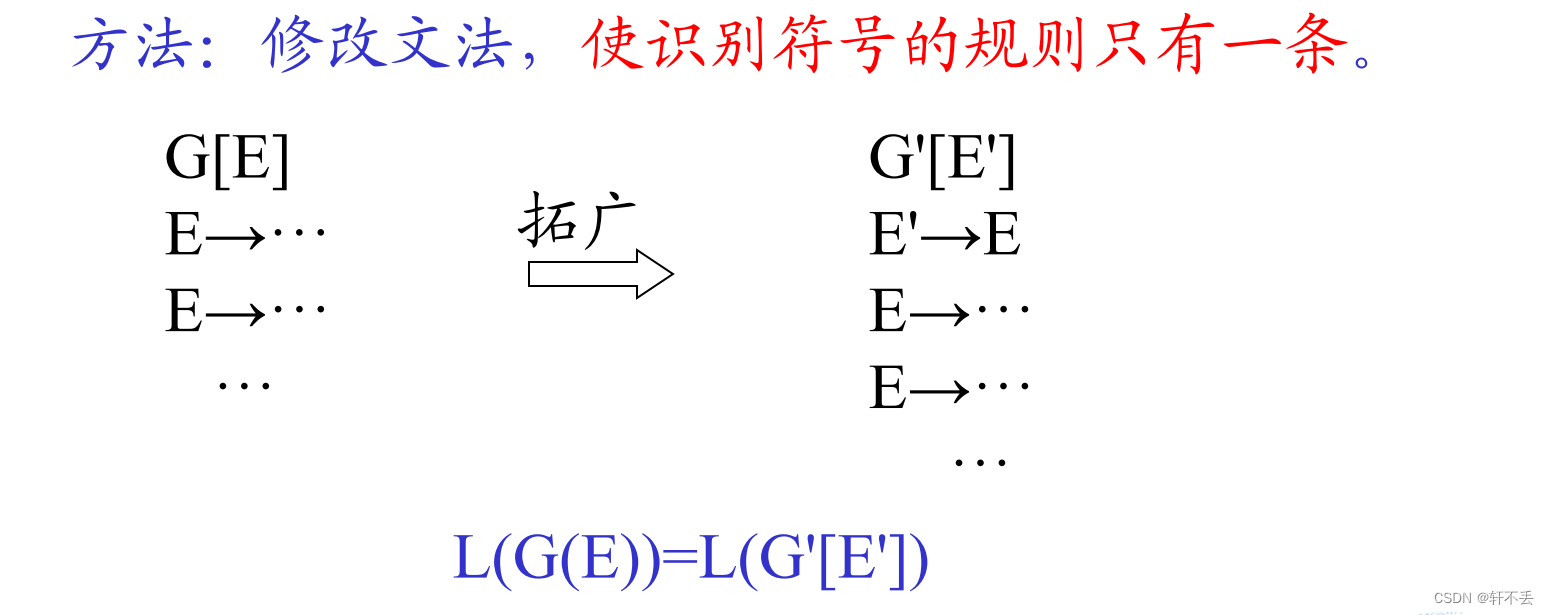
- 将文法拓广
目的:使构造出来的分析表只有一个接受状态,这是为了实现的方便。
- 根据文法列出所有的项目
- 将有关项目组合成集合,即DFA中的状态;
所有状态再组合成一个集合,即LR(0)项目集规范族
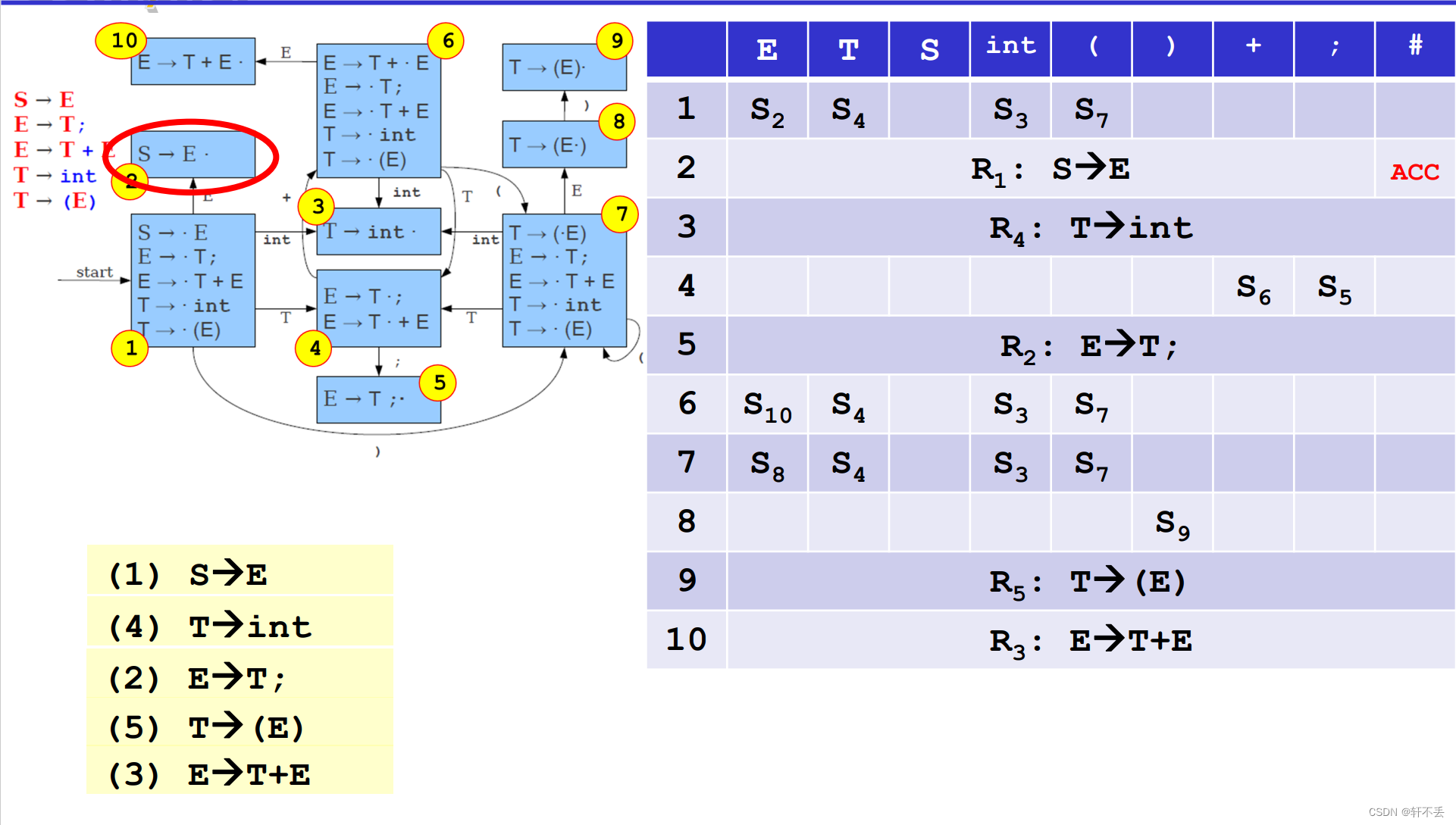
举例分析:

3 将有关项目组成项目集,所有项目集构成的集合即为LR(0)
为实现这一步,先定义:
• 项目集闭包closure
• 状态转移函数GOTO


4、局限性
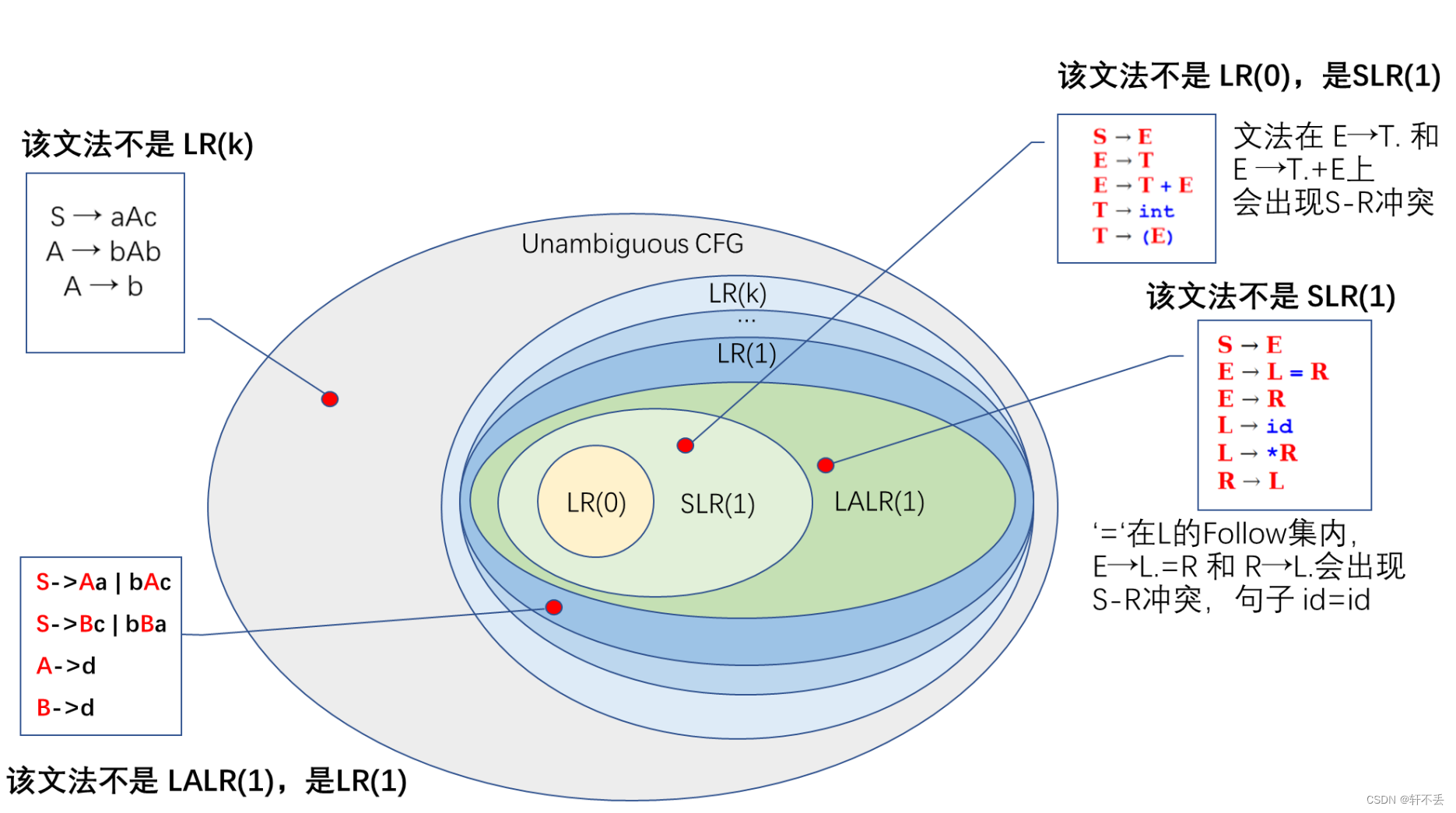
会存在两种冲突,导致LR(0)识别不出来
- Shift-Reduce冲突
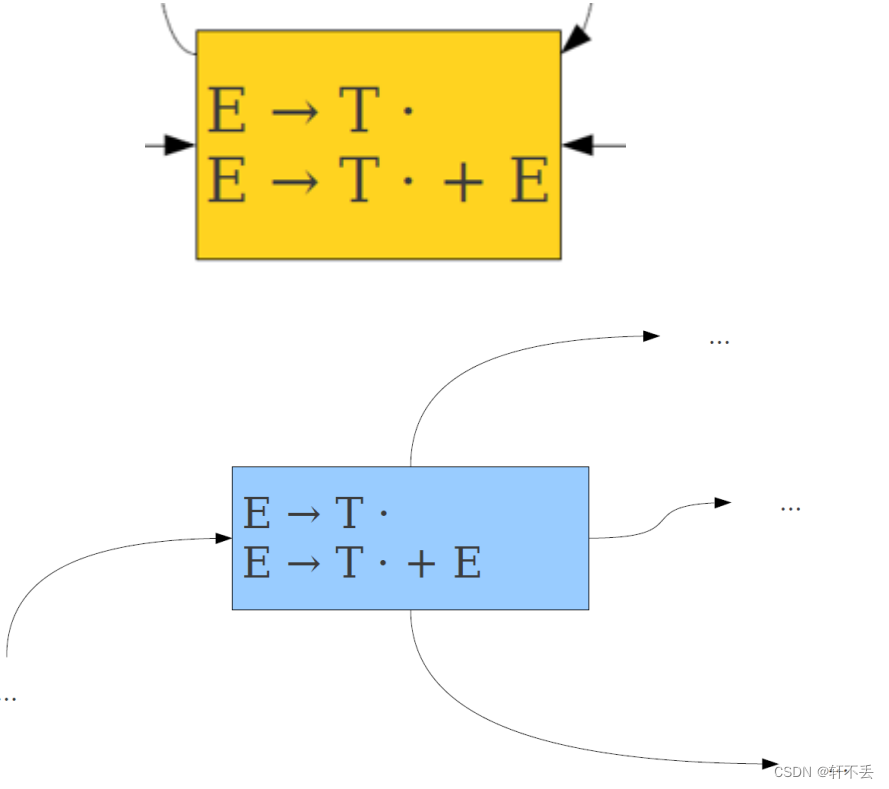
- Reduce-Reduce冲突
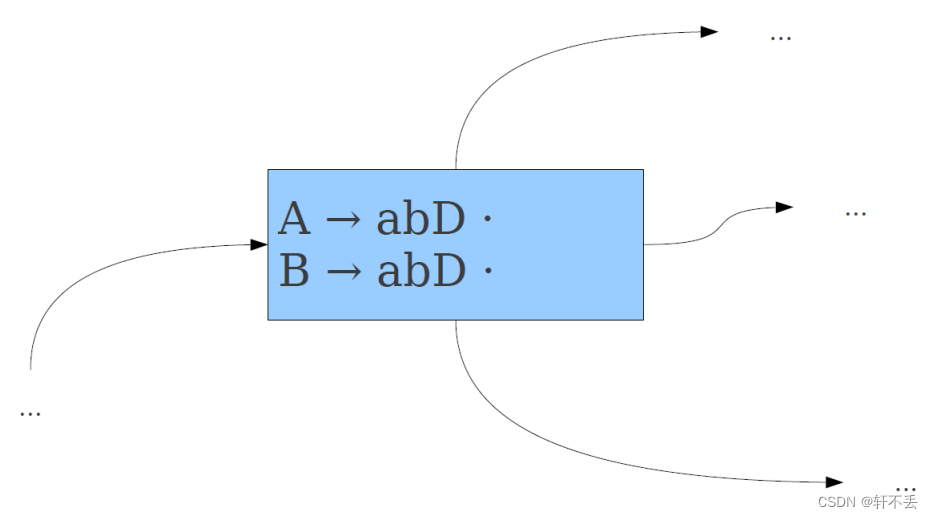
因此需要采用偷看解决问题, L R ( 0 ) → L R ( 1 ) LR(0) → LR(1) LR(0)→LR(1)
三、LR(1)分析法
通过“偷看”一个右侧符号,在遇到冲突时辅助决定。
思路:将状态区分的更加细致,构造LR(1)的状态机。
优点就是可以将状态区分的更加细致,构造LR(1)的状态机。
优势:功能强大!任何LR(0)、LL(1)、确定型CFL、LL(k)、LR(k)都有LR(1)的等价文法。
主要问题:状态爆炸,实用性差。
四、SLR(1):简单LR分析法
1、基本思想
由DFA构造出的SLR分析表,在造表时, 只需向前看一个符号就能确定分析的动作是移进还是归约,所以称为SLR(1)分析表,简称SLR分析表,使用SLR分析表的分析器叫SLR分析器,兼有LR(0)和LR(1)的优点,放弃一些精度。
在LR(0)的基础上,只针对冲突进行处理。
当发生 S-R冲突时,根据FOLLOW集合确定S还是R
2、分析思路
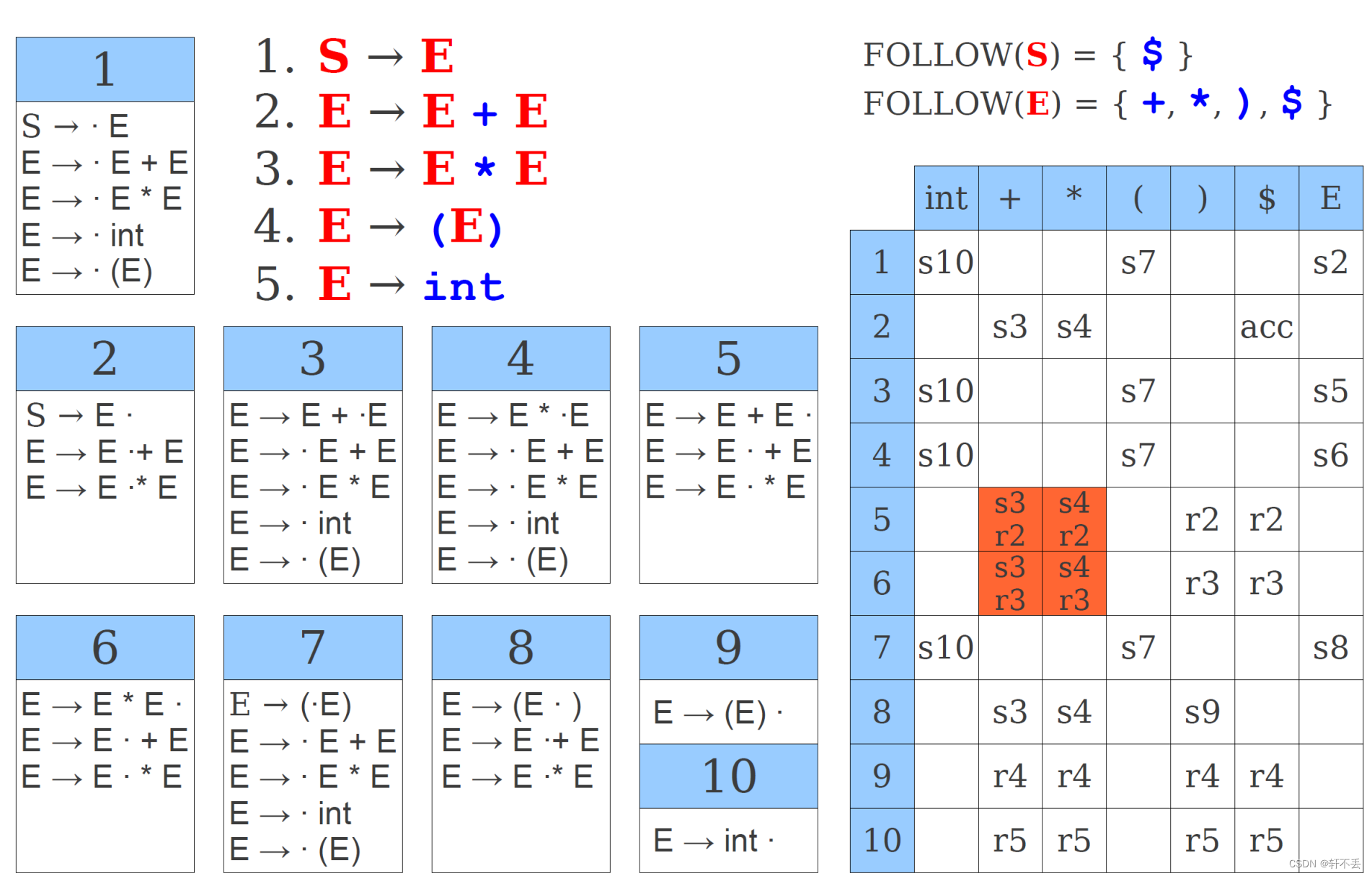
1)构建表
先构造LR(0)的自动机,GOTO表。
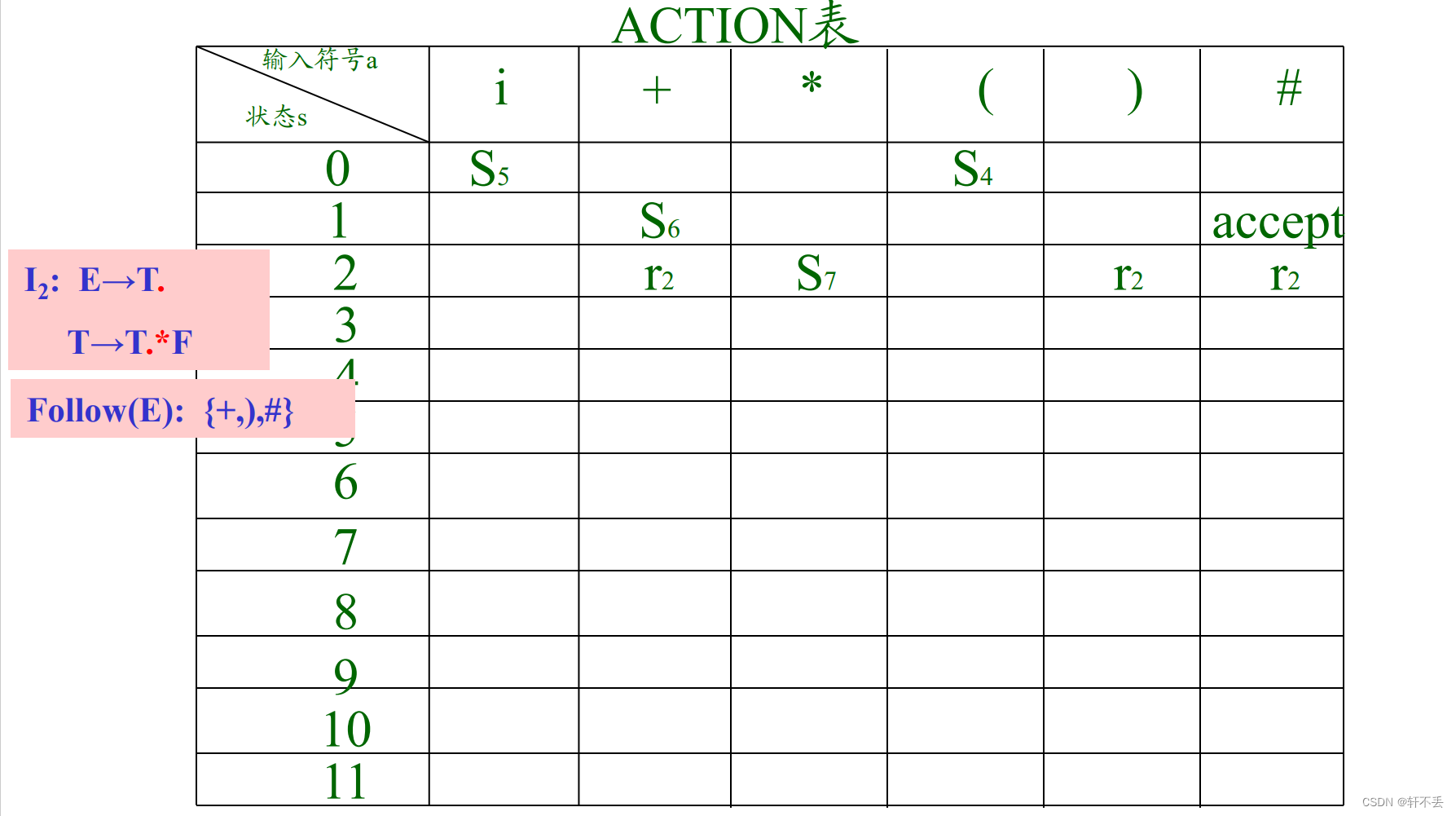
2)SLR求ACTION表
- 求出文法每个非终结符的FOLLOW集合
- 若项目 A → α . a β ∈ k A→α.aβ ∈k A→α.aβ∈k,且 a ∈ V t a ∈V_t a∈Vt ,则置 A C T I O N [ k , a ] = s ACTION[k,a] = s ACTION[k,a]=s (移进)
- 若项目 A → α . ∈ k A→ α.∈k A→α.∈k, 那么对输入符号 a a a,若 a ∈ F O L L O W ( A ) a∈FOLLOW(A) a∈FOLLOW(A),则置 A C T I O N [ k , a ] = r j ACTION[k,a]=r_j ACTION[k,a]=rj,其中 A → α A→ α A→α为文法 G ’ G’ G’的第j个产生式。
- 若项目 E ’ → E . ∈ k E’→E.∈k E’→E.∈k, 则置 A C T I O N ACTION ACTION[ k , k , k,#] = a c c e p t =accept =accept
- 空白格,均置error
看到 f o l l o w follow follow应该做规约(已经跳出表达式了)
3、局限性
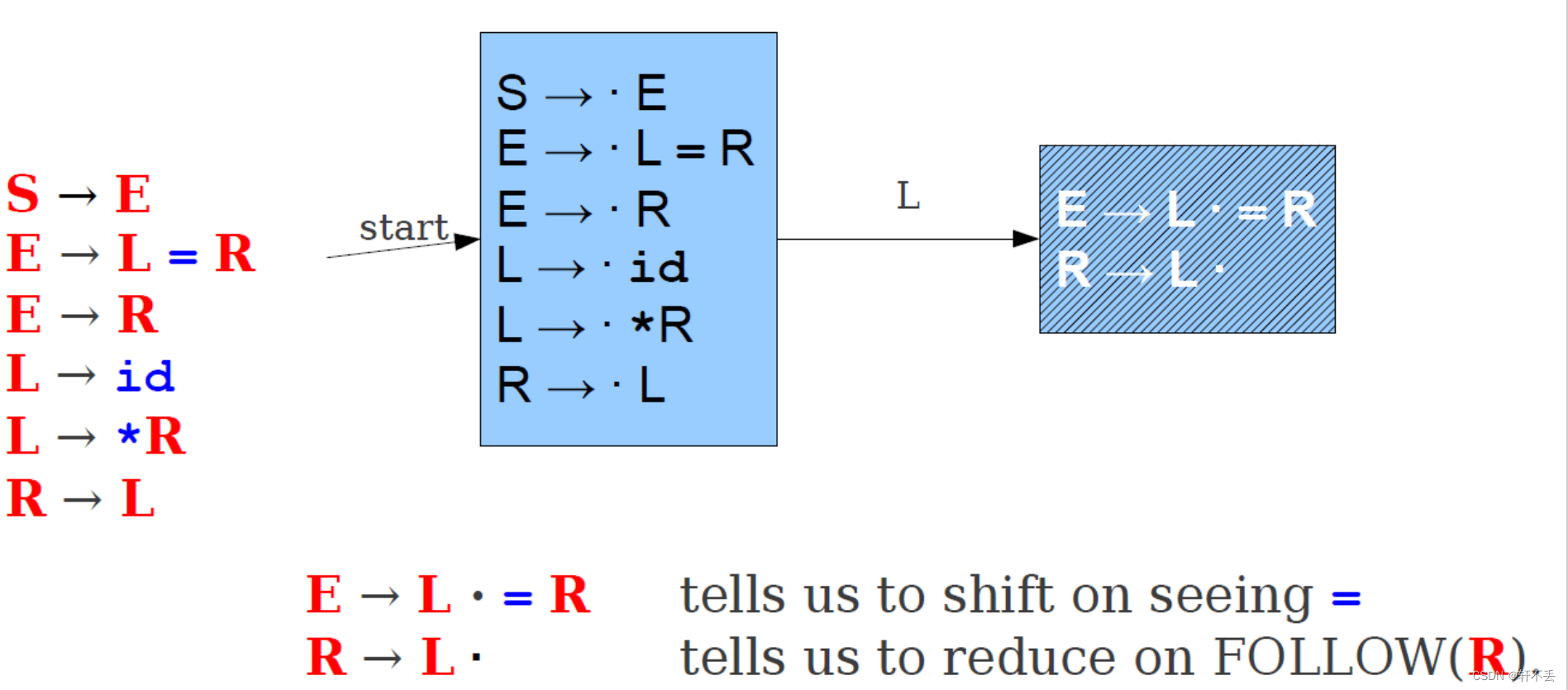
F
O
L
L
O
W
(
R
)
FOLLOW(R)
FOLLOW(R)中有=,应该做规约,但是碰到=,E中表达式应该移进,因此还是冲突。
对文法G,若应用上述算法所造出的分析表具有多重定义入口,分析动作不唯一, 则文法G就不是SLR的,需要用别的方法来构造分析表。如下图
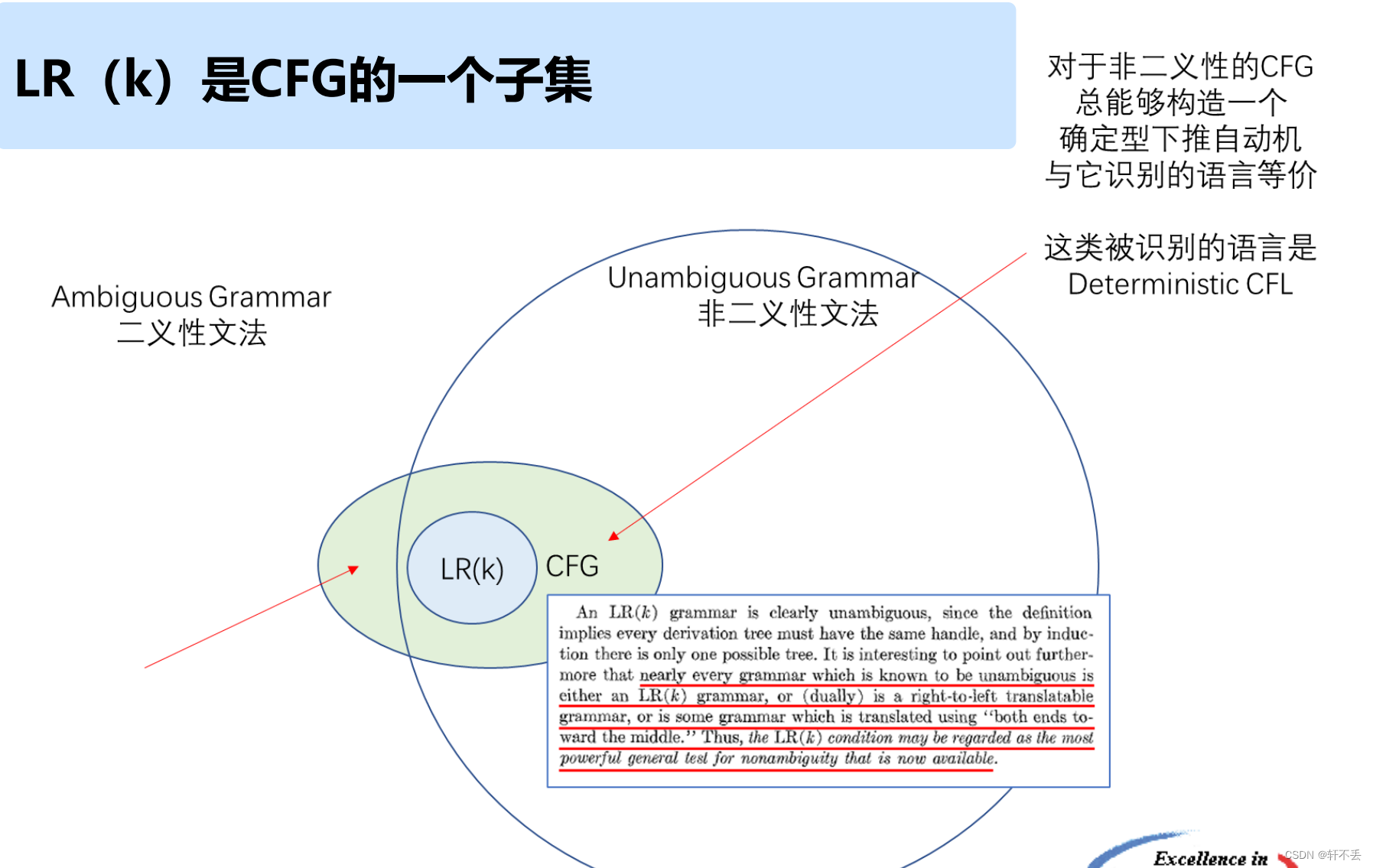
五、彩蛋
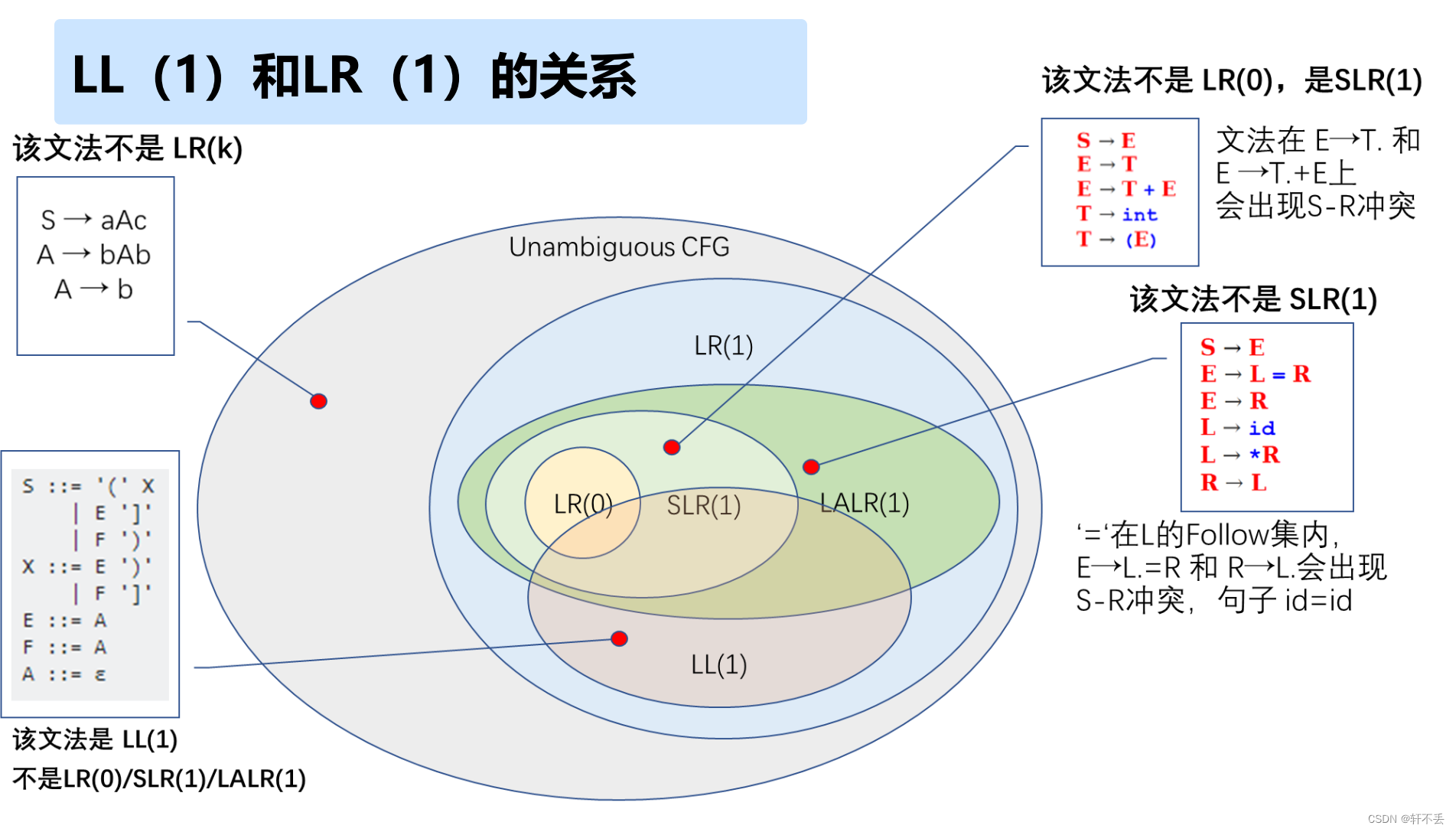
L L ( k ) LL(k) LL(k)是无二义性的, L L ( k ) LL(k) LL(k)文法识别的语言都是确定型下推自动机所识别的语言,但反之,不能保证任何一个确定型下推自动机 D P D A DPDA DPDA与 L L ( k ) LL(k) LL(k)等价
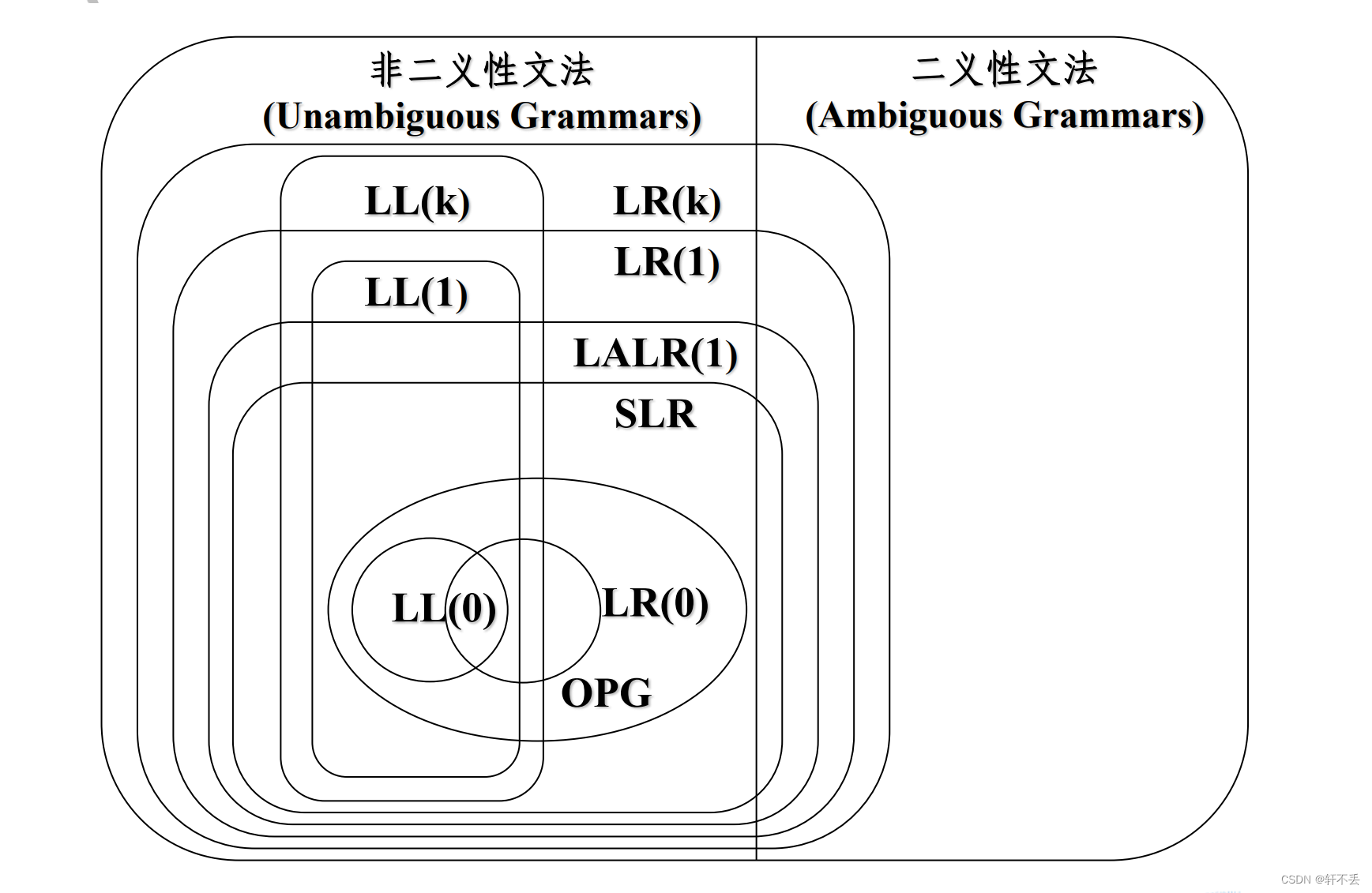
LL(k)文法总是一个LR(k)文法 ,
L
L
(
k
)
LL(k)
LL(k)是
L
R
(
k
)
LR(k)
LR(k)的子集
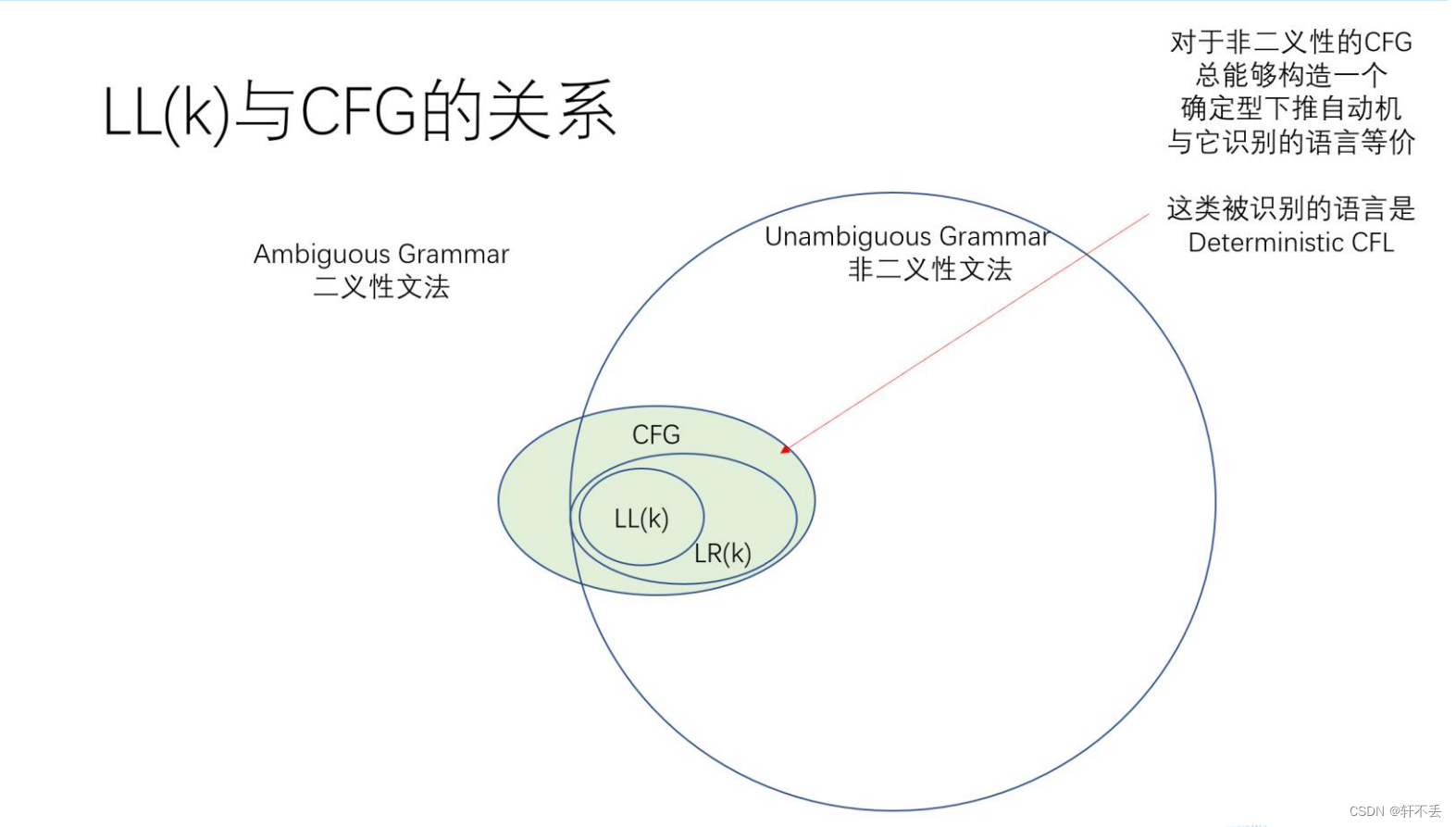
定义上看,LR(0), LR(1), LR(k), SLR(1), LALR(1)等,要求构造出来的分析表是“确定性”的,也就是分析表不允许存在冲突,无二义性!