文章目录
- 总览
- 算法
- 编写代码:
- recursive_bezier()的实现
- Bezier()函数的实现
- 提高部分:反走样
总览
Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中,你需要实现 de Casteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当你正确实现该算法时,你可以支持绘制由更多点来控制的 Bézier 曲线)。
你需要修改的函数在提供的 main.cpp 文件中。
• bezier:该函数实现绘制 Bézier 曲线的功能。它使用一个控制点序列和一个OpenCV::Mat 对象作为输入,没有返回值。它会使 t 在 0 到 1 的范围内进行迭代,并在每次迭代中使 t 增加一个微小值。对于每个需要计算的 t,将调用另一个函数 recursive_bezier,然后该函数将返回在 Bézier 曲线上 t处的点。最后,将返回的点绘制在 OpenCV ::Mat 对象上。
• recursive_bezier:该函数使用一个控制点序列和一个浮点数 t 作为输入,实现 de Casteljau 算法来返回 Bézier 曲线上对应点的坐标。
算法
De Casteljau 算法说明如下:
- 考虑一个 p0, p1, … pn 为控制点序列的 Bézier 曲线。首先,将相邻的点连接起来以形成线段。
- 用 t : (1 − t) 的比例细分每个线段,并找到该分割点。
- 得到的分割点作为新的控制点序列,新序列的长度会减少一。
- 如果序列只包含一个点,则返回该点并终止。否则,使用新的控制点序列并转到步骤 1。
使用[0,1] 中的多个不同的 t 来执行上述算法,你就能得到相应的 Bézier 曲线。
编写代码:
我们先把源代码的naive_bezier画Bezier曲线的程序跑通
mkdir build
cd build
cmake ..
make
./BezierCurve
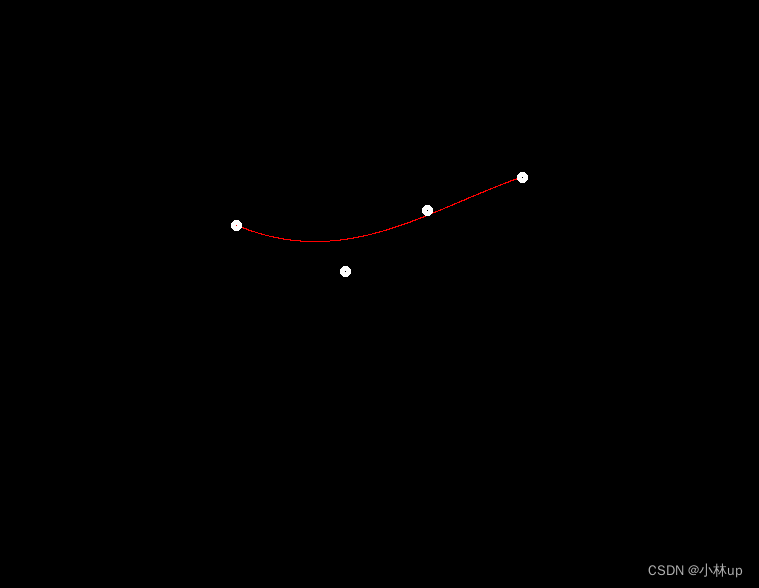
然后我们注释掉main函数里的naive_bezier(control_points, window);,实现自己的Bezier曲线绘制。
recursive_bezier()的实现
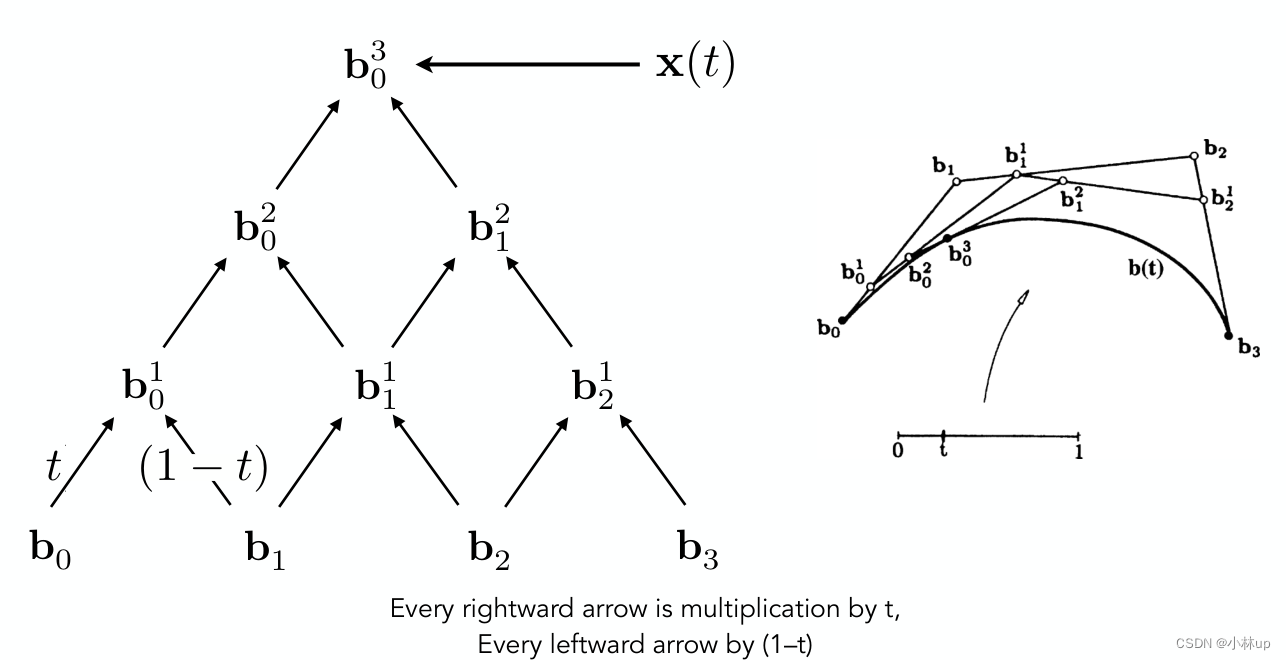
我们在recursive_bezier()函数中获得根据t获得贝塞尔曲线的点,这里不同于直接使用多项式(naive_bezier使用的是多项式的方法),使用递归算法,递归的返回条件是最终递归数组的长度为1(下图对应的是
b
0
3
\mathbf{b}_0^3
b03),这时候返回结果。如果没有达到返回条件,就进入下一次递归,传进递归计算后的数组(数组的长度减1):
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t)
{
// TODO: Implement de Casteljau's algorithm
int len = control_points.size();
if (len == 1)
return control_points[0];
std::vector<cv::Point2f> lerp_control_points(len - 1, cv::Point2f(0.0, 0.0));
for (int i = 0; i < len - 1; ++i)
{
lerp_control_points[i] = t * control_points[i] + (1 - t) * control_points[i + 1];
}
return recursive_bezier(lerp_control_points, t);
}
Bezier()函数的实现
我们在bezier()函数里从0到1遍历所有的t,然后使用前面写的recursive_bezier()获得Bezier曲线点的坐标,然后在图上该点的位置涂上颜色即可。
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = recursive_bezier(control_points, t) ;
window.at<cv::Vec3b>(point.y, point.x)[1] = 255; //显示是绿色
}
}
绿色的曲线通过同样的make命令可以得到:
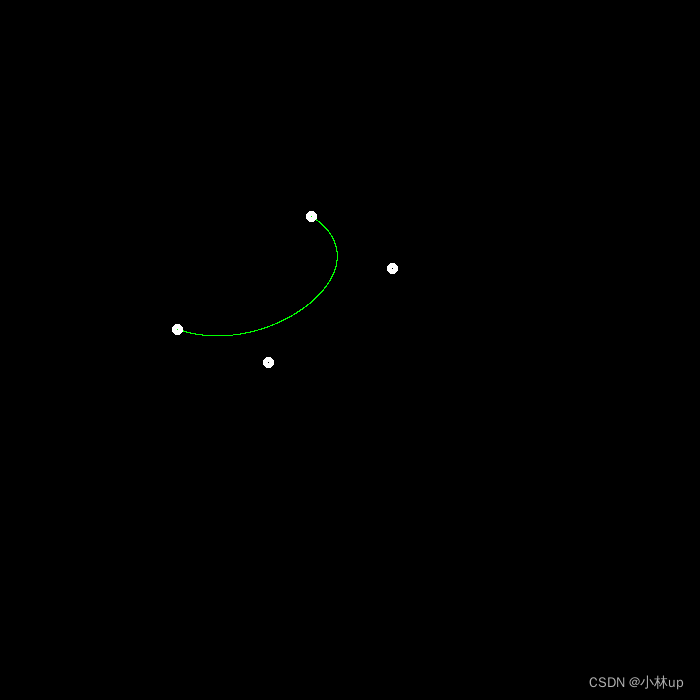
把naive_bezier(control_points, window);取消注释可以看到黄色的Bezier曲线
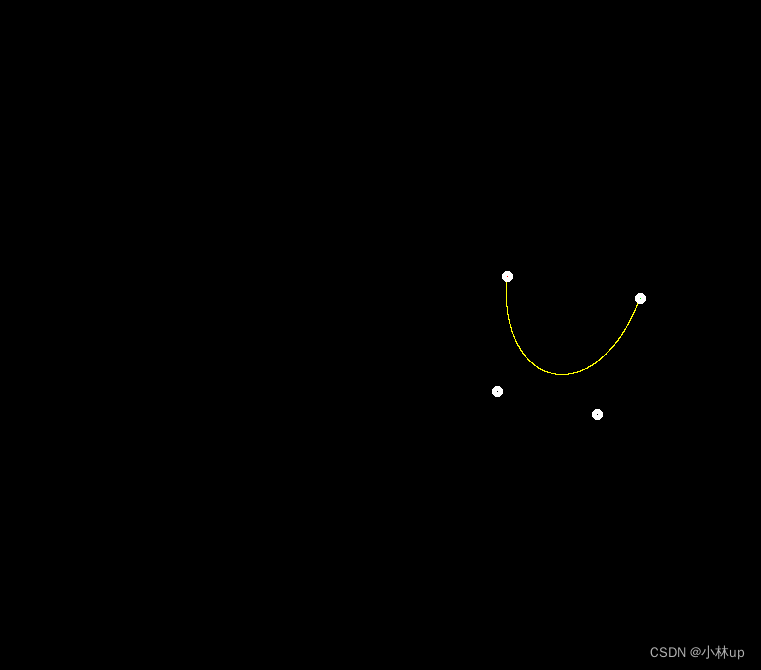
但可以看到锯齿比较明显
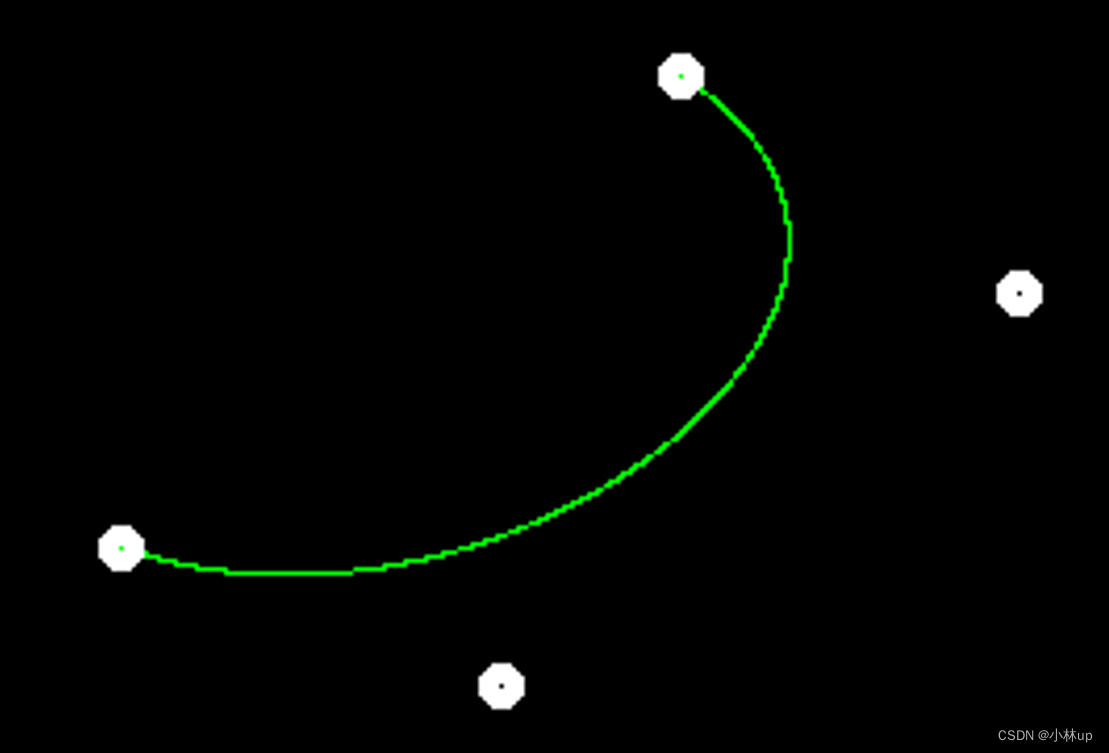
提高部分:反走样
提高部分要求使用反走样,题目提示说:
对于一个曲线上的点,不只把它对应于一个像素,你需要根据到像素中心的距离来考虑与它相邻的像素的颜色。
也就是说离像素越近颜色越深,离像素越远颜色越浅。
这里参考的是作业四得到这样的结果是否满足要求?里xuyonglai的思路,我们首先要找到和Bezier曲线点(point.x,point,y)最临近的四个像素,曲线点所在的像素很好找,其他三个像素该怎么找呢?这里类似采用四舍五入的方法,判断(point.x,point,y)靠近它所在像素的哪一侧,以此来确定其他三个像素的方向,然后我们就可以确定四个像素的坐标了,其中代码中的p0是最临近的像素,其他的p1,p2,p3依次是其他三个像素。然后定义一个pvec存放这三个临近的像素,依次给这其他三个近邻像素着色,这里取了最大值是因为如果这次计算的像素的颜色是偏暗的绿色,但是这个像素上次有重复计算(靠近曲线绿色的比重更大),替换为暗色可能会让反走样的效果变差。这种方法也有一定的缺点,就是只能对黑色的背景(RGB三个分量都是0)起作用,但是其他背景颜色直接取max最大值就不太行了。

void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
// TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's
// recursive Bezier algorithm.
for (double t = 0.0; t <= 1.0; t += 0.001)
{
auto point = recursive_bezier(control_points, t) ;
window.at<cv::Vec3b>(point.y, point.x)[1] = 255; //显示是绿色
float xDelta = point.x - std:: floor(point.x);
float yDelta = point.y - std:: floor(point.y);
int xDir = xDelta < 0.5f ? -1 : 1;
int yDir = yDelta < 0.5f ? -1 : 1;
cv::Point2f p0 = cv::Point2f(std::floor(point.x) + 0.5f, std::floor(point.y) + 0.5f);
cv::Point2f p1 = cv::Point2f(std::floor(point.x + xDir * 1.0f) + 0.5f, std::floor(point.y) + 0.5f);
cv::Point2f p2 = cv::Point2f(std::floor(point.x) + 0.5f, std::floor(point.y + yDir * 1.0f) + 0.5f);
cv::Point2f p3 = cv::Point2f(std::floor(point.x + xDir * 1.0f) + 0.5f, std::floor(point.y + yDir * 1.0) + 0.5f);
std::vector<cv::Point2f> pvec;
pvec.push_back(p1);
pvec.push_back(p2);
pvec.push_back(p3);
float d1 = std::sqrt(std::pow(p0.x - point.x, 2) + std::pow(p0.y - point.y, 2));
for (auto& p: pvec)
{
float dp = std::sqrt(std::pow(p.x - point.x, 2) + std::pow(p.y - point.y, 2));
float weight = d1 / dp;
float colorG = window.at<cv::Vec3b>(p.y, p.x)[1];
colorG = std::fmax(colorG, weight * 255.0);
window.at<cv::Vec3b>(p.y, p.x)[1] = (int)colorG;
}
}
}
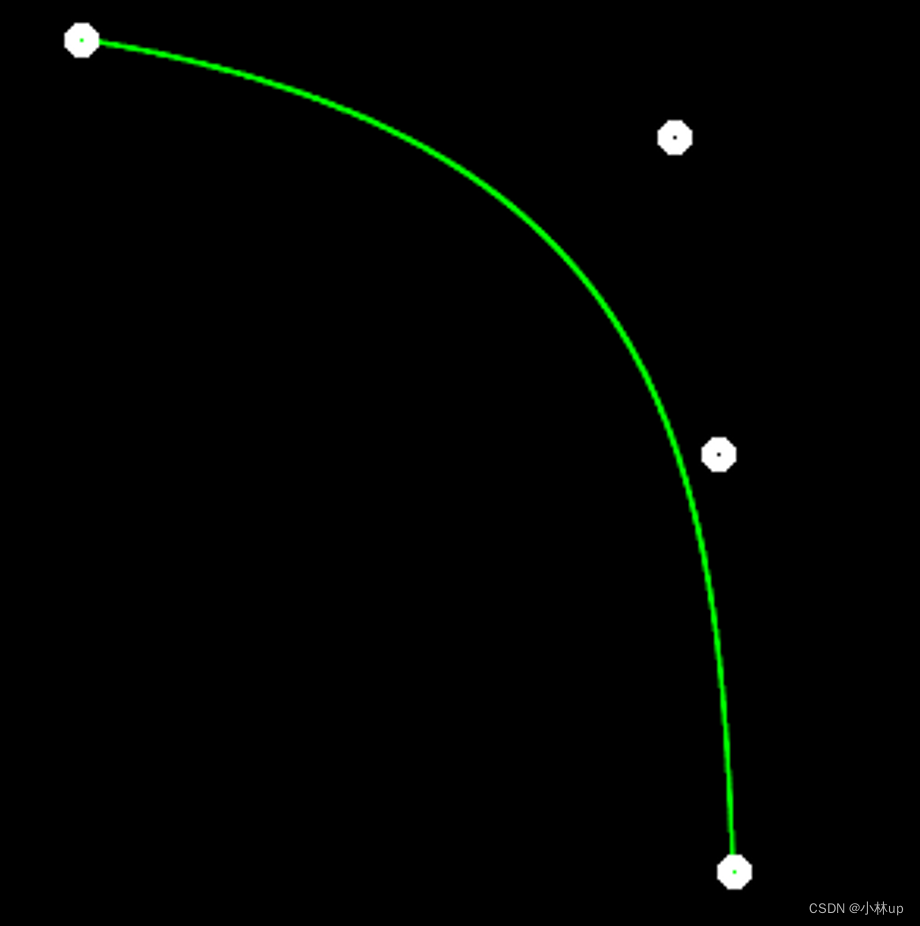
可以看到反走样有了较好的效果。
其他反走样的方法也可以看这篇文章:Games 101 | 作业4 + Bezier Curve + 反走样 + 双线性插值,距离和颜色的值(RGB分量的值越接近1越饱和)成反比,所以用最大距离减去像素中心和曲线点的距离也可以构造反比的函数,权重需要在0到1之间,还是一样我们使用所有的最大距离减像素中心和曲线点的距离的值的和作为分母,使用大距离减去特定像素中心和曲线点的距离作为分子计算特定像素的权重,这里就不写代码了,思路是差不多的。
其他参考:
The Beauty of Bresenham’s Algorithm【介绍了Bresenham’s 算法来实现反走样】
A Rasterizing Algorithm for Drawing Curves【上面网站的pdf的说明】







![[2024区块链开发入门指引] - 比特币运行原理](https://img-blog.csdnimg.cn/img_convert/679a4160ce14887093a56d47d4e30d01.jpeg#pic_center)