目录
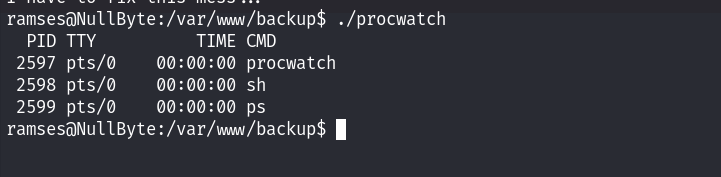
求分布律里的未知数
例1
例2
根据X的分布律写Y的分布律
例3
根据(X,Y)的分布律写Z的分布律
例4
根据(X,Y)的分布律写边缘分布律
例5
X与Y相互独立时的联合分布律
例6
根据分布律求期望、方差
例7
求分布律里的未知数
例1
已知X的分布律为
,试求k
X -2 0 2 P 0.4 0.3 k
解
0.4+0.3+k=1 → k = 0.3
例2
设二维随机变量(X,Y)的联合分布律为
X\Y 0 1 0 1 a 解
2/3+1/12+a+1/12=1 → a=1/6
根据X的分布律写Y的分布律
例3
已知X的分布律为
求Y=X*X+1的分布律
X -2 0 2 P 0.4 0.3 0.3
方法:
在分布律中X以及X的取值是可以同时变化的
例如
X*2 -2*2 0*2 2*2 P 0.4 0.3 0.6 本题我们需要下面这个表
X*X (-2)*(-2) 0*0 2*2 P 0.4 0.3 0.3
X*X+1 (-2)*(-2)+1=5 0*0+1 2*2+1=5 P 0.4 0.3 0.3 解
Y 1 5 P 0.3 0.7
根据(X,Y)的分布律写Z的分布律
例4
已知(X,Y)的分布律为
X\Y -1 0 1 0 0 0 1 0 求Z=XY的分布律
X\Y -1 0 1 0 Z=0*(-1)=0 Z=0*0=0 Z=0*1=0 1 Z=1*(-1)=1 Z=1*0=0 Z=1*1=0
Z -1 0 1 P
根据(X,Y)的分布律写边缘分布律
例5
已知(X,Y)的分布律为
求随机变量X,Y的边缘分布律
X\Y -1 0 1 0 0 0 1 0
解
X 0 1 P +
=
Y -1 0 1 P 根据(X,Y)分布律,对应的值的概率为该行或该列的概率的和
X与Y相互独立时的联合分布律
例6
设随机变量X与Y相互独立,下表列出了二维随机变量(X,Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值,试将其余数值填入表中的空白处
方法一:
X\Y y1 y2 y3 P{X=xi} x1 ? ? ? x2 ? ? ? P{Y=yj} ? ? ?
每一列的和等于最下面的数P{Y=yj},每一行的和等于最右边的数P{X=xi}
方法二:
右下角的数为1,最下边所有数P{Y=yj}的和等于1,最右边所有数P{X=xi}的和等于1
方法三:
当X与Y相互独立时,每个空的概率都等于其最下面的数P{Y=yj}×其最右边的数P{X=xi}
解
X\Y y1 y2 y3 P{X=xi} x1 x2 P{Y=yj} 1
根据分布律求期望、方差
例7
已知X的分布律为
X -2 0 2 P 0.4 0.3 0.3 Y的分布律为
试求(EX、EY、E(X^2)、E(Y^3+1)、E(3X+5Y+7))求期望、(DX)求方差
Y 1 5 P 0.3 0.7
解
对于单一字母的期望
期望的值为每列上面的数×下面的数相加
EX=-2×0.4+0×0.3+2×0.3=-0.2
EY=1×0.3+5×0.7=3.8E(X^2)=(-2)×(-2)×0.4+0×0×0.3+2×2×0.3=2.8
X*X (-2)*(-2)=4 0*0 2*2=4 P 0.4 0.3 0.3
Y^3+1 1^3+1=2 5^3+1=126 P 0.3 0.7
E(Y^3+1)=(1^3+1)×0.3+(5^3+1)×0.7=88.8
对于E(3X+5Y+7)
方法:
E(aX+bY+c)=aEX+bEY+c
E(3X+5Y+7)=3EX+5EY+7=3×(-0.2)+5×3.8+7=25.4
对于DX
方法:
DA=
DX=E(X^2)-(EX)^2=2.8-(-0.2)^2=2.76
![[2024区块链开发入门指引] - 比特币运行原理](https://img-blog.csdnimg.cn/img_convert/679a4160ce14887093a56d47d4e30d01.jpeg#pic_center)