文章目录
- 1.问题描述
- 2.难度等级
- 3.热门指数
- 4.解题思路
- 4.1 暴力
- 4.2 排序
- 4.3 哈希表
- 4.4 空间复杂度为 O(1) 的哈希表
- 4.5 置换
- 参考文献
1.问题描述
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
提示:
1 <= nums.length <= 5 * 10^5
-2^31 <= nums[i] <= 2^31 - 1
2.难度等级
Hard。
这道题很简单,但是题目的要求是 O(n) 的时间复杂度和 O(1) 空间复杂度,所以难度上升到了 Hard。
3.热门指数
★★★★☆
4.解题思路
4.1 暴力
最容易想到的做法是暴力法。
我们可以从 1 开始依次枚举正整数,并遍历数组,判断其是否在数组中。
时间复杂度:
如果数组的长度为 n,时间复杂度为 O(n^2)。
所以该算法时间复杂度不满足题目要求。
空间复杂度:
O(1)。只需要常数级别的空间存储若干变量。
下面以 Golang 为例给出实现。
func firstMissingPositive(nums []int) int {
p := 1
for {
exist := false
for i := 0; i < len(nums); i++ {
if nums[i] == p {
p++
exist = true
break
}
}
if !exist {
return p
}
}
}
4.2 排序
我们可以对数组排序,然后遍历数组,找到第一个不在 nums 中的正整数。
时间复杂度:
O(nlogn),排序一般时间复杂度为 O(nlogn),然后遍历排序后的数组,最坏时间复杂度为 O(n),所以总的时间复杂度为 O(nlogn)。
所以该算法时间复杂度不满足题目要求。
空间复杂度:
O(1)。只需要常数级别的空间存储若干变量。
下面以 Golang 为例给出实现。
func firstMissingPositive(nums []int) int {
slices.Sort(nums)
p := 1
for i := 0; i < len(nums); i++ {
if nums[i] == p {
p++
}
}
return p
}
4.3 哈希表
我们可以将数组所有的数放入哈希表,随后从 1 开始依次枚举正整数,并判断其是否在哈希表中。
时间复杂度:
如果数组的长度为 n,那么时间复杂度为 O(n)。
空间复杂度:
需要哈希表存储数组所有元素,空间复杂度为 O(n)。
所以该算法空间复杂度不满足题目要求。
下面以 Golang 为例给出实现。
func firstMissingPositive(nums []int) int {
m := make(map[int]struct{}, len(nums))
for _, v := range nums {
m[v] = struct{}{}
}
for p := 1; ; p++ {
if _, ok := m[p]; !ok {
return p
}
}
}
4.4 空间复杂度为 O(1) 的哈希表
题目要求空间复杂度需要 O(1),所以不能使用额外的哈希表存储数组中的元素。
我们将目光放到数组本身。
实际上,对于一个长度为 n 的数组,其中没有出现的最小正整数只能在 [1,n+1] 中。我们可以利用数组本身,将数组中大于等于 1 小于等于 n 的正整数,在数组中打上标记。
打完标记后,遍历数组,如果下标 i 没有被打上标记,那么 i+1 就是数组中缺失的第一个正整数。
如果数组所有下标均被打上标记,那么 n+1 就是数组中缺失的第一个正整数。
如何给数组下标打上标记呢?
由于我们只在意 [1,n] 中的数,因此我们可以先对数组进行遍历,把不在 [1,n] 范围内的数修改成任意一个大于 n 的数(例如 n+1)。这样一来,数组中的所有数就都是正数了,因此我们就可以将「标记」表示为「负号」。
算法的流程如下:
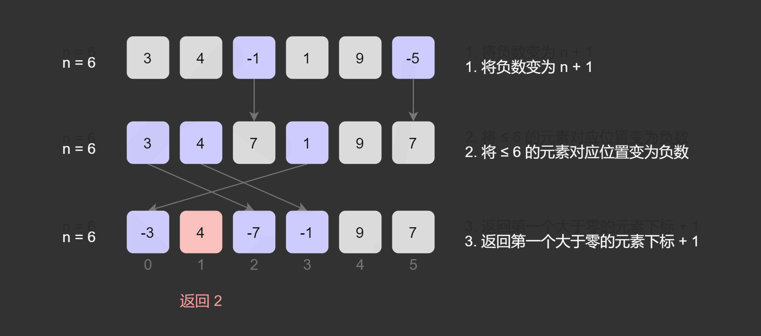
-
我们将数组中所有小于等于 0 的数修改为 n+1。
-
我们遍历数组中的每一个数 x,它可能已经被打了标记,因此原本对应的数为 |x|,其中 || 为绝对值符号。如果 |x|∈[1,n],那么我们给数组中的第 |x|−1 位置的数添加一个负号。注意如果它已经有负号,不需要重复添加。
-
在遍历完成之后,如果数组中的每一个数都是负数,那么答案是 n+1,否则答案是第一个正数的下标加 1。
时间复杂度:
三次遍历数组,第一次遍历将数组中所有非正数变成 n+1。第二次遍历给数组下标打标记。第三次遍历获取没有打标记的下标。所以时间复杂度是 O(n),满足题目要求。
空间复杂度:
没有使用额外的存储空间,所以是 O(1),满足题目要求。
下面以 Golang 为例给出实现。
func firstMissingPositive(nums []int) int {
// 将数组中所有小于等于 000 的数修改为 n+1。
for i, v := range nums {
if v <= 0 {
nums[i] = len(nums) + 1
}
}
// 给数组下标打标记。
for _, v := range nums {
abs := int(math.Abs(float64(v)))
if abs >= 1 && abs <= len(nums) {
if nums[abs-1] > 0 {
nums[abs-1] = -nums[abs-1]
}
}
}
// 遍历数组,寻找未打标记的下标。
for i, v := range nums {
if v > 0 {
return i + 1
}
}
return len(nums) + 1
}
4.5 置换
除了打标记以外,我们还可以使用置换的方法,将给定的数组「恢复」成下面的形式:
如果数组中包含 x∈[1,n],那么恢复后,数组的第 x−1 个元素为 x。
在恢复后,数组应当有 [1, 2, …, n] 的形式,但其中有若干个位置上的数是错误的,每一个错误的位置就代表了一个缺失的正数。以题目中的示例二 [3, 4, -1, 1] 为例,恢复后的数组应当为 [1, -1, 3, 4],我们就可以知道缺失的数为 2。
那么我们如何将数组进行恢复呢?我们可以对数组进行一次遍历,对于遍历到的数 x=nums[i],如果 x∈[1,n],我们需要将 x 放在数组中的 x−1 的位置,因此交换 nums[i] 和 nums[x−1],这样 x 就出现在了正确的位置。
在完成交换后,新的 nums[i] 可能还在 [1,n] 的范围内,我们需要继续进行交换操作,直到 x∉[1,n]。
注意到上面的方法可能会陷入死循环。如果 nums[i] 恰好与 nums[x−1] 相等,那么就会无限交换下去。此时我们有 nums[i]=x=nums[x−1],说明 x 已经出现在了正确的位置。因此我们可以跳出循环,开始遍历下一个数。
时间复杂度:
由于每次的交换操作都会使得某一个数交换到正确的位置,因此交换的次数最多为 n,整个方法的时间复杂度为 O(n)。
空间复杂度:
没有使用额外的存储空间,所以是 O(1)。
下面以 Golang 为例给出实现。
func firstMissingPositive(nums []int) int {
n := len(nums)
for i := range nums {
for nums[i] > 0 && nums[i] <= n && nums[i] == nums[nums[i]-1] {
nums[i], nums[nums[i]-1] = nums[nums[i]-1], nums[i]
}
}
for i, v := range nums {
if v != i+1 {
return i + 1
}
}
return len(nums) + 1
}
参考文献
41. 缺失的第一个正数 - LeetCode