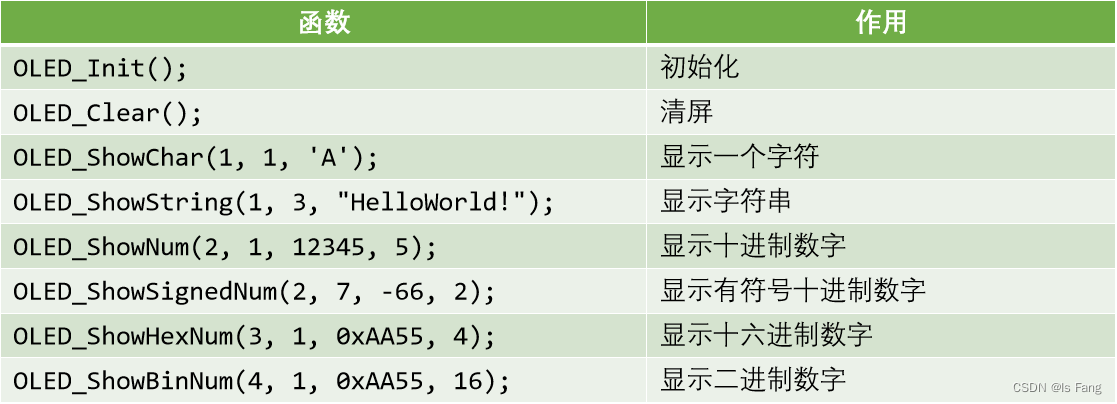
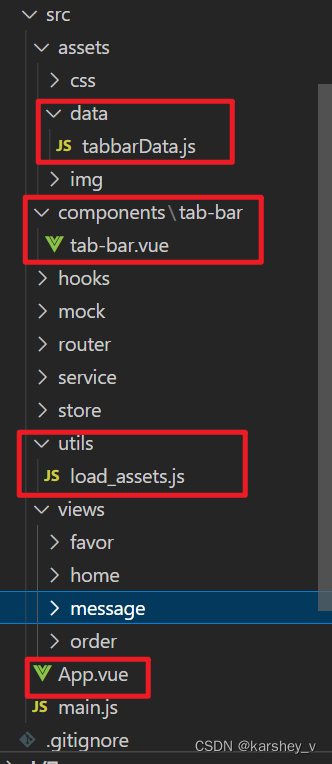
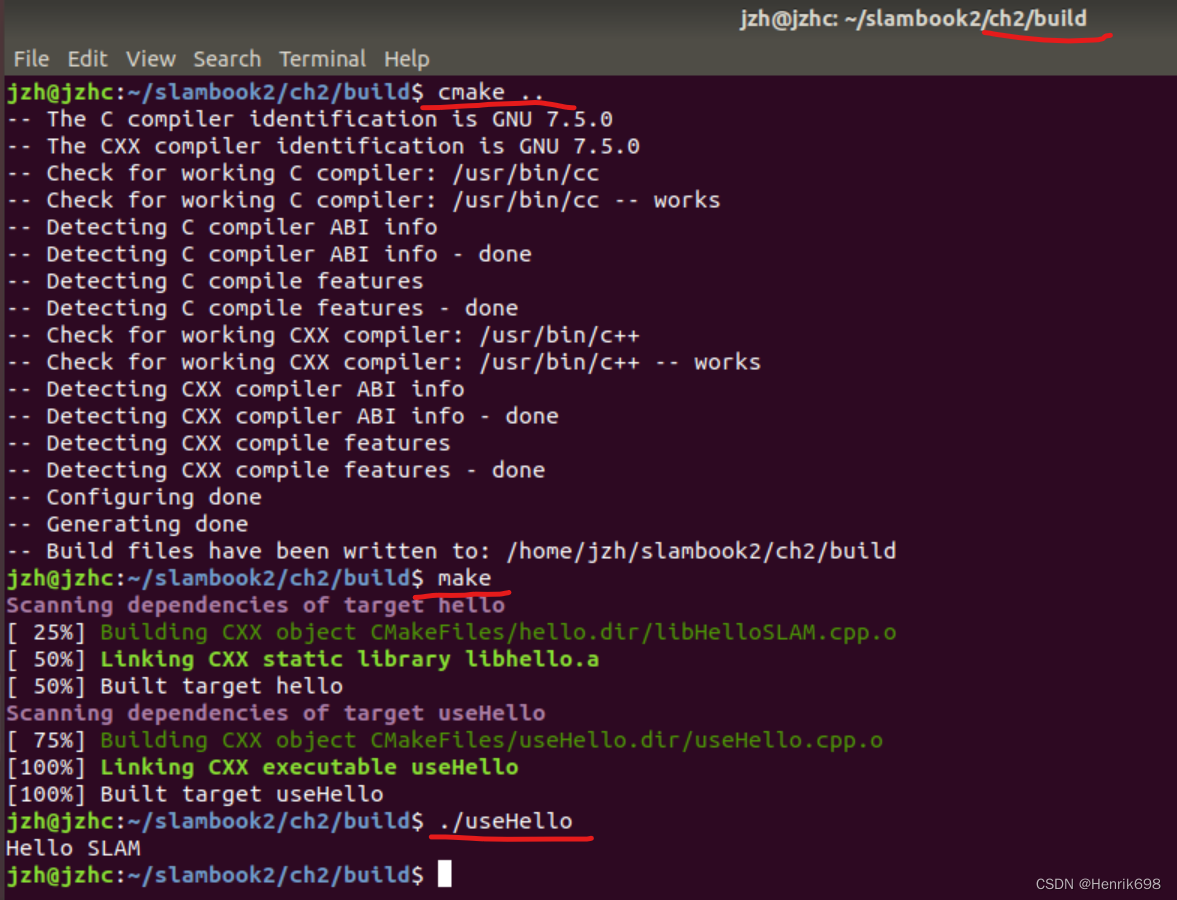
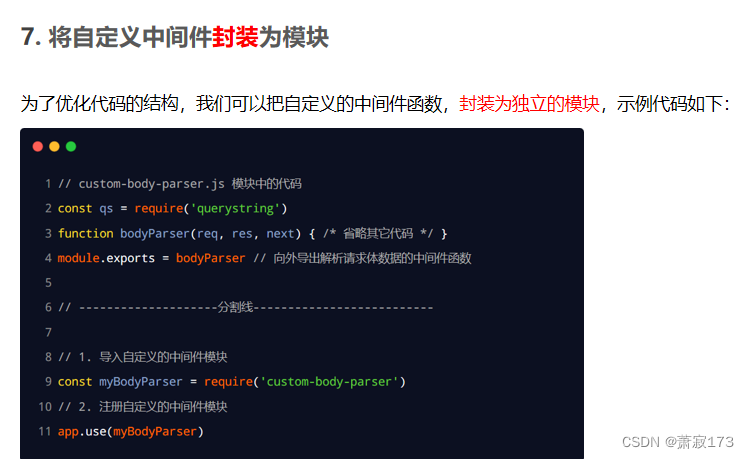
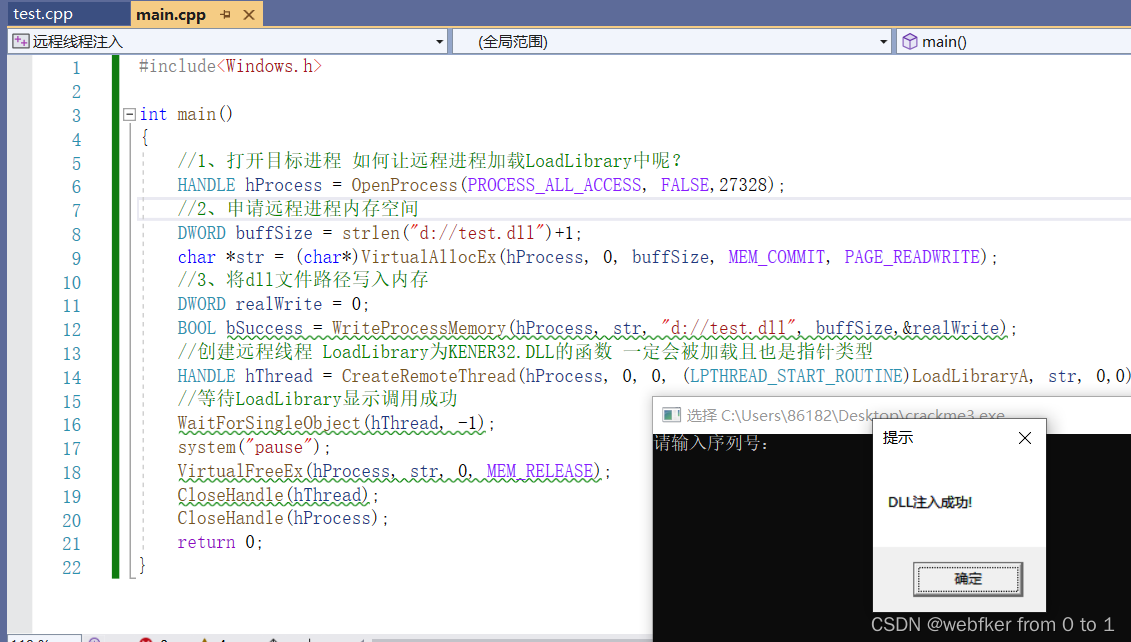
​

编辑

添加图片注释，不超过 140 字（可选）

外点也即是我们所说的粗差，是因为在实际工程当中由于人为因素或者测量设备等因素造成的测量值与实际情况相比误差较大。然后从高斯分布的角度来说就是大于3σ以外的数据。本篇博客将主要讲解ransac和m估计。

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

Ransac的流程一定要清楚，其就是通过不断调整自己的参数来使得内点的数量尽量多。

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

上面的公式里面确定k与p 的关系，也即需要预估一下计算多少次ransac可以达到预期的效果。

M估计

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

M估计就是将二次项用其他函数来代替，其代替的目的是在误差较大时降低其增长的速度。

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

没有仔细推

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

在推导M估计的时候，当使用当前工作点计算Y矩阵，便称为迭代重加权最小二乘 IRLS

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

RANSAC与最小二乘的区别：

最小二乘法尽量去适应包括外点在内的所有点。而RANSAC得出一个仅仅用内点计算出模型，并且概率还足够高。但是，RANSAC不能保证结果一定正确（只有一定的概率得到可信的模型），为了保证算法有足够高的合理概率，必须小心选择算法的参数。对于外点数量较多的数据集，RANSAC的效果远优于直接的最小二乘法。

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

处理外点的方法主要为RANSAC和M估计，其中ransac的流程要知道，其是通过不断调整模型的参数，也即不断调整拟合直线的参数来保证获得更多的内点数量。然后根据最终得到的模型来剔除掉外点(也即粗差)。然后M估计是在二次项误差较大的情况下，使用其他函数来替代二次函数，进而使得尽管误差很大，但是其不会对模型的目标函数起主导作用。也即削弱了误差较大对目标函数的影响。

然后对ransac和最小二乘的区别，首先最小二乘需要把外点很好地拟合在直线中，而ransac是剔除外点的。但是ransac是以概率的角度来得到结果的，因此不一定得到正确结果。最后针对外点数量较多的模型，ransac的效果是比较好的。

下面是IRLS和自适应估计，这些都是基于M估计的基础上，根据计算中的一些情况创造的方法。其本质还是从M估计开始，降低误差很大时对模型的影响。