【owt-server】一些构建项目梳理
news2026/2/14 4:50:01
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1345317.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
【PyQt】(自定义类)QIcon派生,更易用的纯色Icon
嫌Qt自带的icon太丑,自己写了一个,主要用于纯色图标的自由改色。 当然,图标素材得网上找。 Qt原生图标与现代图标对比:
没有对比就没有伤害 Qt图标 网络素材图标 自定义类XJQ_Icon:
from PyQt5.QtGui import QIc…
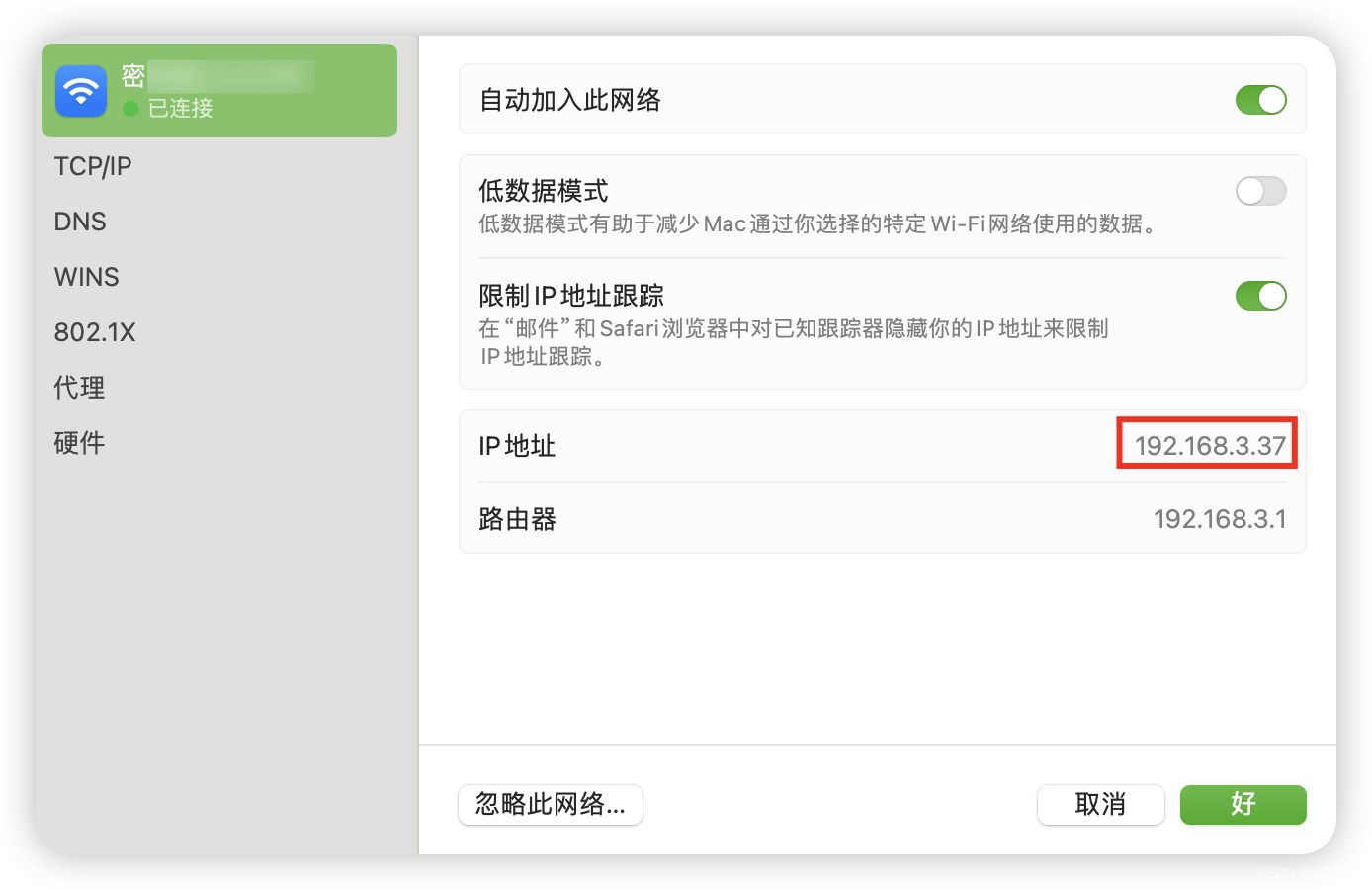
MacBook查看本机IP
嘚吧嘚
其实这也不是什么困难的问题,但是今年刚刚入坑Mac,外加用的频率不是很高,每次使用的时候都查,用完就忘,下次用的时候再查🤮。真的把自己恶心坏了🙈。
所以写篇文章记录一下ᾒ…
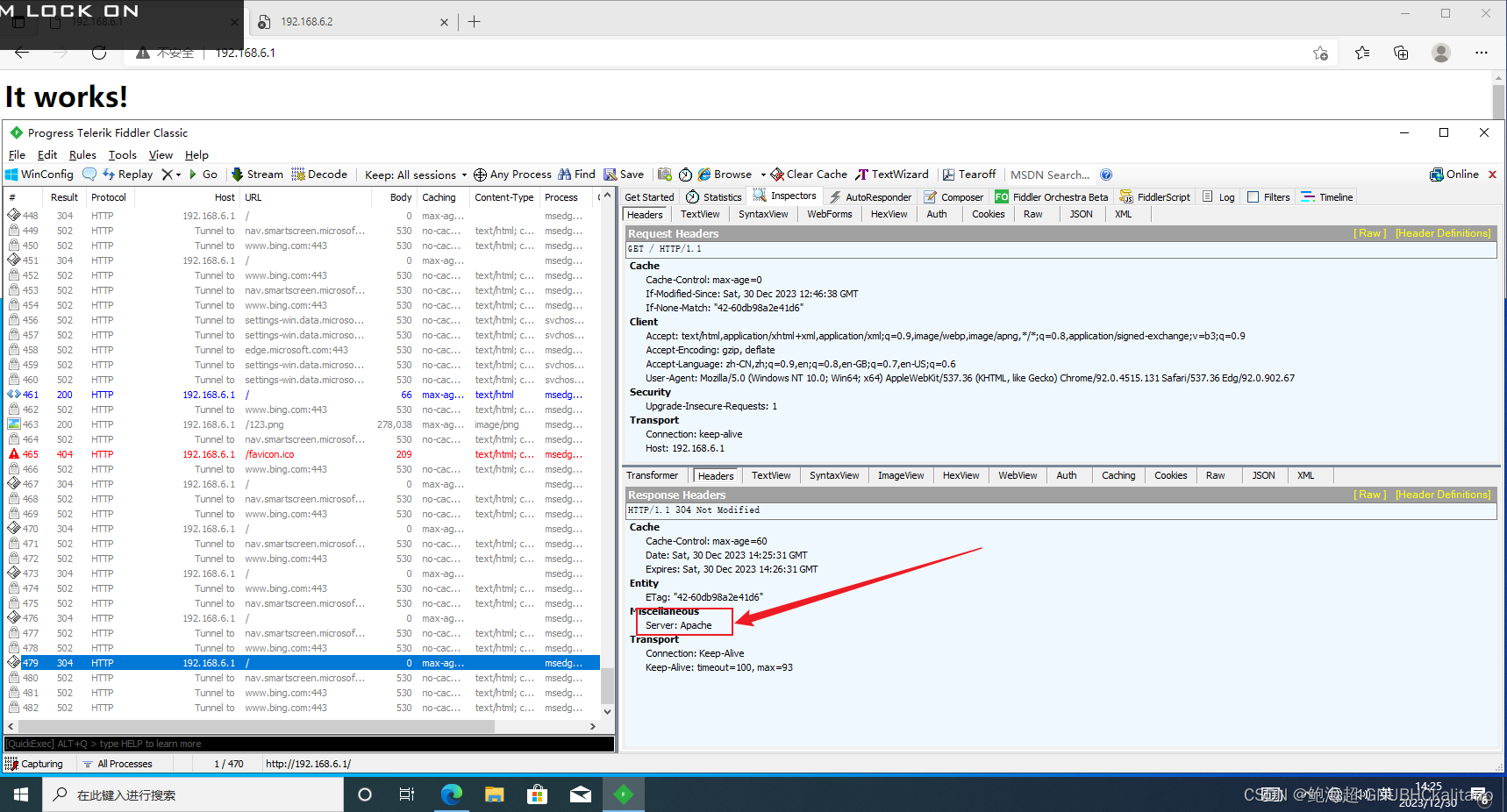
Linux:apache优化(4)—— 隐藏版本号
运行环境
yum -y install apr apr-devel cyrus-sasl-devel expat-devel libdb-devel openldap-devel apr-util-devel apr-util pcre-devel pcre gcc make zlib-devel
源码包配置
./configure --prefix/usr/local/httpd --enable-cgi --enable-rewrite --enable-so --enabl…
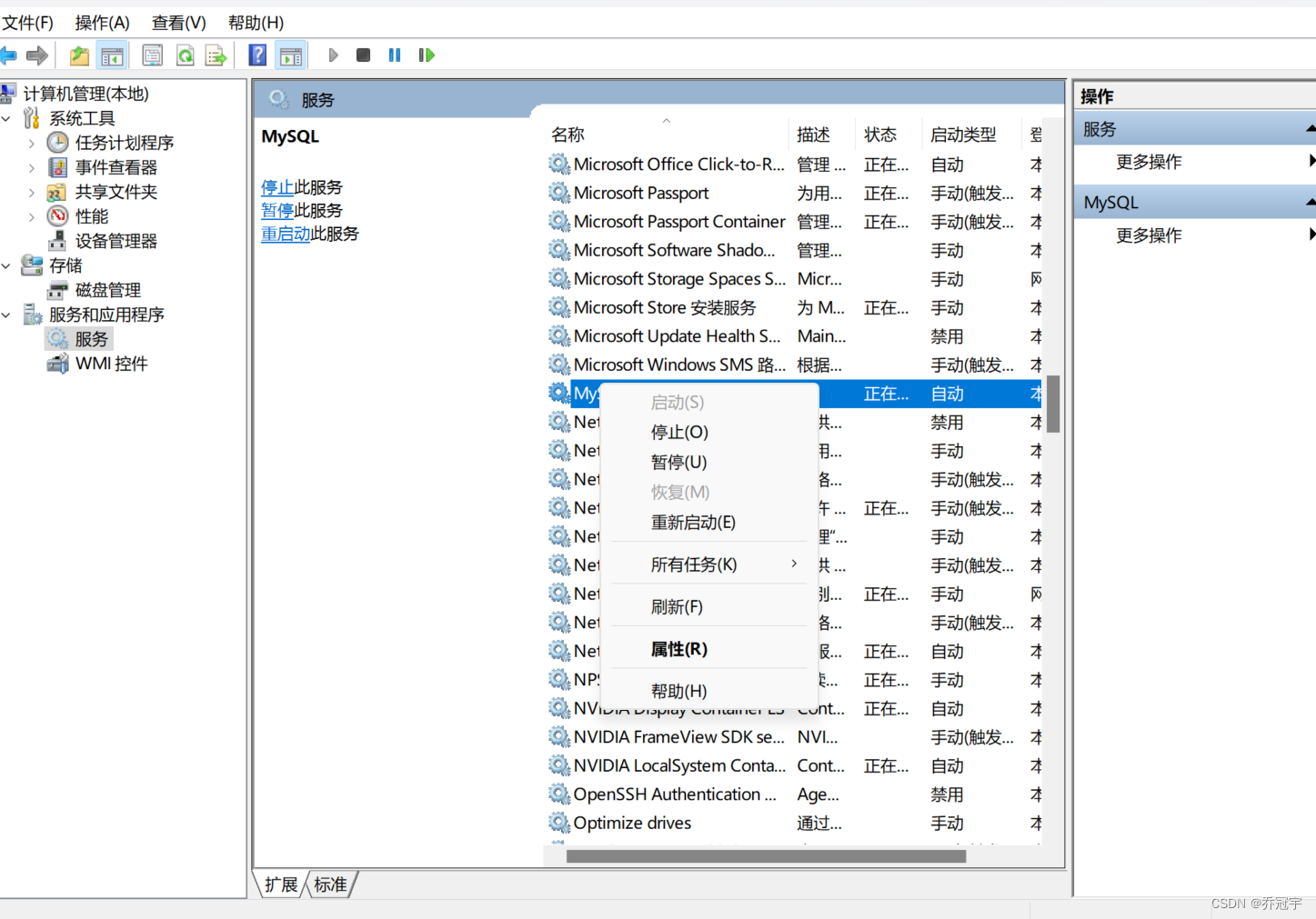
MySQL数据库的安装与环境配置
下载
下载MySQL8 安装
解压 配置MySQL环境变量
系统环境变量path D:\ProgramFiles\mysql-8.0.20-winx64\bin
1.点击属性 2.点击高级系统设置 3.点击环境变量 4.在系统变量中找到path 注意这里不是用户变量
5.新建后输入解压的地址 MySQL初始化和启动
以管理员身份运行cmd…
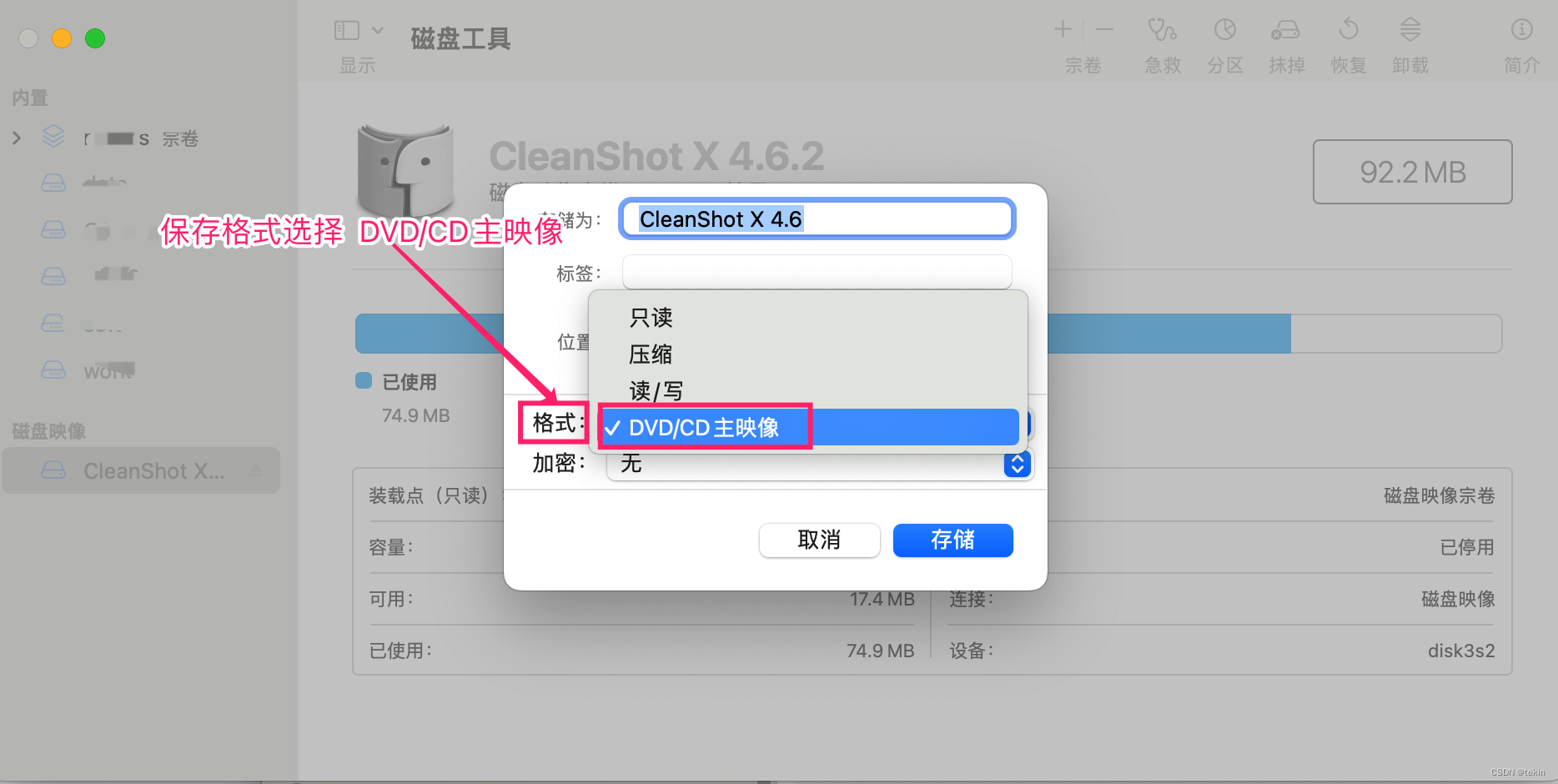
macos下转换.dmg文件为 .iso .cdr文件的简单方法
为了让镜像文件在mac 和windows平台通用, 所以需要将.dmg格式的镜像文件转换为.iso文件, 转换方法也非常简单, 一行命令即可
hdiutil convert /path/to/example.dmg -format UDTO -o /path/to/example.iso
转换完成后的文件名称默认是 example.iso.cdr 这里直接将.cdr后缀删…
Efficient Classification of Very Large Images with Tiny Objects(CVPR2022补1)
文章目录 Two-stage Hierarchical Attention SamplingOne-stageTwo-Stage内存需求 Efficient Contrastive Learning with Attention Sampling Two-stage Hierarchical Attention Sampling
一阶段缩放是hw,提取的特征是h1w1, 二阶段缩放是uv(…
Vue中的默认插槽详解
Vue中的默认插槽详解 在 Vue 中,插槽(Slot)是一种非常强大且灵活的机制,用于在组件中插入内容。Vue 提供了两种类型的插槽:默认插槽(Default Slot)和具名插槽(Named Slot)…
24、Web攻防-通用漏洞SQL注入MYSQL跨库ACCESS偏移
文章目录 一、SQL注入原理 脚本代码在与数据库进行数据通讯时(从数据库取出相关数据进行页面显示),使用预定义的SQL查询语句进行数据查询。能通过参数传递自定义值来实现SQL语句的控制,执行恶意的查询操作,例如查询…
[Angular] 笔记 20:NgContent
chatgpt:
在Angular中,NgContent是用于内容投影(Content Projection)的一个重要概念。它允许你在一个组件中插入内容,并将这些内容投影到另一个组件中。
当你在一个组件中使用<ng-content></ng-content>标签时&…
Python新手教程 —— Hello, World!
文章目录 Hello, World!作者自述关于本系列什么是编程语言什么是Python安装Python运行Python3解释器IDLE编写代码文件 本文复习Python技术资源分享1、Python所有方向的学习路线2、学习软件3、入门学习视频4、实战案例5、清华编程大佬出品《漫画看学Python》6、Python副业兼职与…
黑马程序员SSM框架-Maven进阶
分模块开发与设计
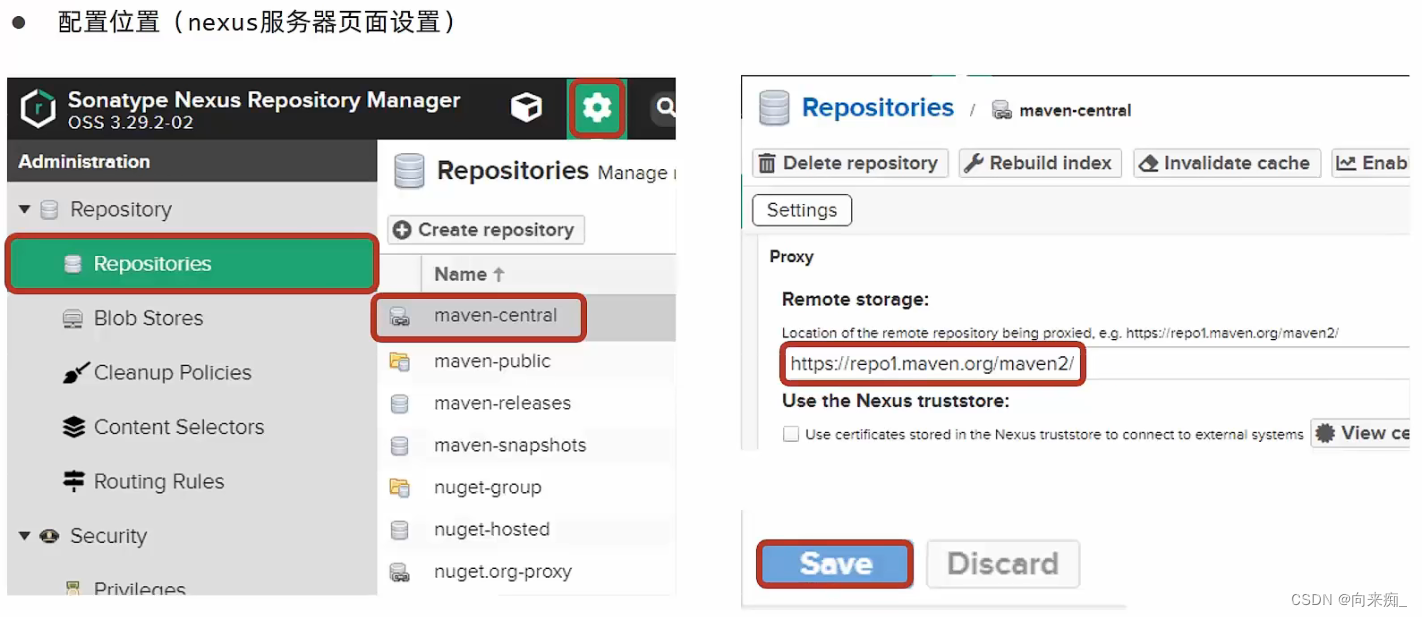
分模块开发意义 分模块开发 依赖管理
依赖传递 依赖传递冲突问题 可以点击红框按钮查看依赖情况。 可选依赖和排除依赖 继承和聚合
聚合 聚合工程开发 继承 聚合和继承的区别 属性
属性的配置与使用 资源文件引用属性 其他属性(了解࿰…
<JavaEE> 协议格式 -- 应用层协议 HTTP
目录
一、HTTP的概念
1)什么是HTTP协议?
2)什么是超文本?
二、HTTP协议格式
三、请求(request)
1) 方法(Method)
1> GET方法
2> POST方法
3> GET和POS…
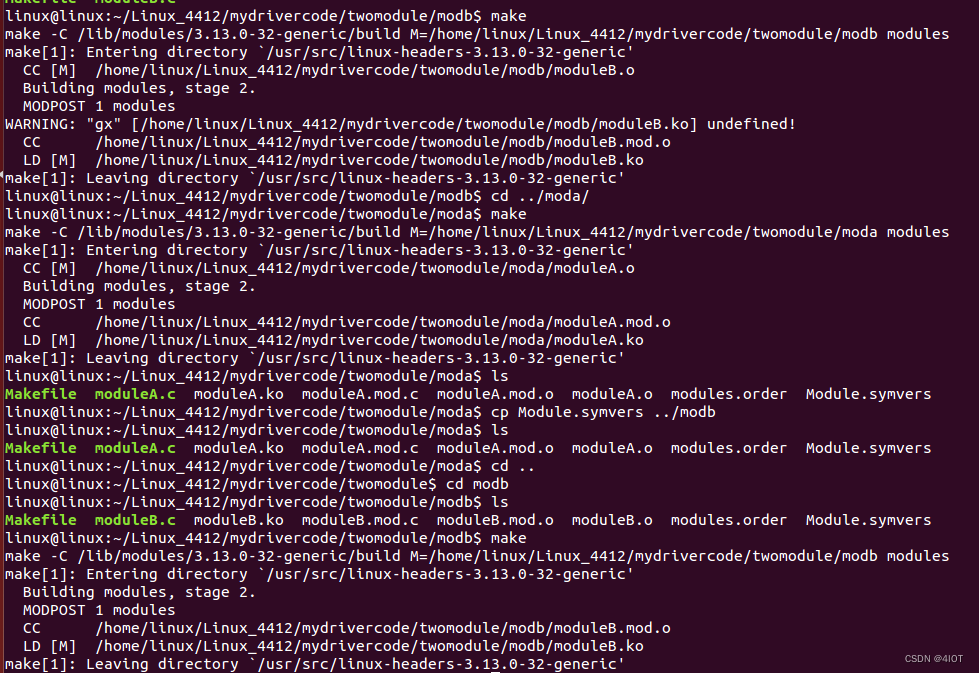
lv13 内核模块参数和依赖
1 模块传参
1.1 模块参数设置
将指定的全局变量设置成模块参数
module_param(name,type,perm);//将指定的全局变量设置成模块参数
/*
name:全局变量名
type:使用符号 实际类型 传参方式bool bool insmod xxx.ko 变量名0 …
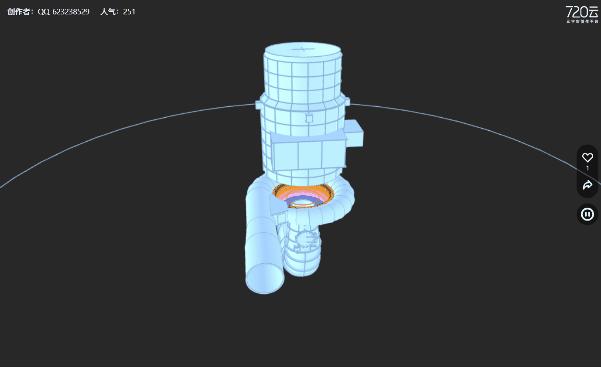
拍照就能建模!手机就能访问! 这个技术正成为宣传新手段!
随着人工智能技术的不断进步,现在可以通过拍摄照片结合AI技术来实现3D模型生成。这种技术的出现, 不仅能更加方便快捷地创建3D模型,而且还能真实复原现实中物件的质感、纹理等。同时,极大地降低了各行业对3D技术的应用门槛&#x…
[Angular] 笔记 24:ngContainer vs. ngTemplate vs. ngContent
请说明 Angular 中 ngContainer, ngTemplate 和 ngContent 这三者之间的区别。
chatgpt 回答: 这三个在 Angular 中的概念是关于处理和组织视图的。
1. ngContainer:
ngContainer 是一个虚拟的 HTML 容器,它本身不会在最终渲染…
二分查找(非朴素)--在排序数组中查找元素的第一个和最后一个位置
个人主页:Lei宝啊
愿所有美好如期而遇 目录
本题链接
输入描述
输出描述
算法分析
1.算法一:暴力求解
2.算法二:朴素二分算法
3.算法三:二分查找左右端点
3.1查找左端点
3.1.1细节一:循环条件
3.1.2细节二…
【详解】KMP算法——每步配图让你打穿KMP
介绍
什么是KMP算法:
KMP算法主要运用串的模式匹配中(简单来说就是在s串中找到一个与t串相等的子串,称为模式匹配)例如s为abcdef,t为bcd,那么就是在s中找到bcd,并返回其在s中的首下标…
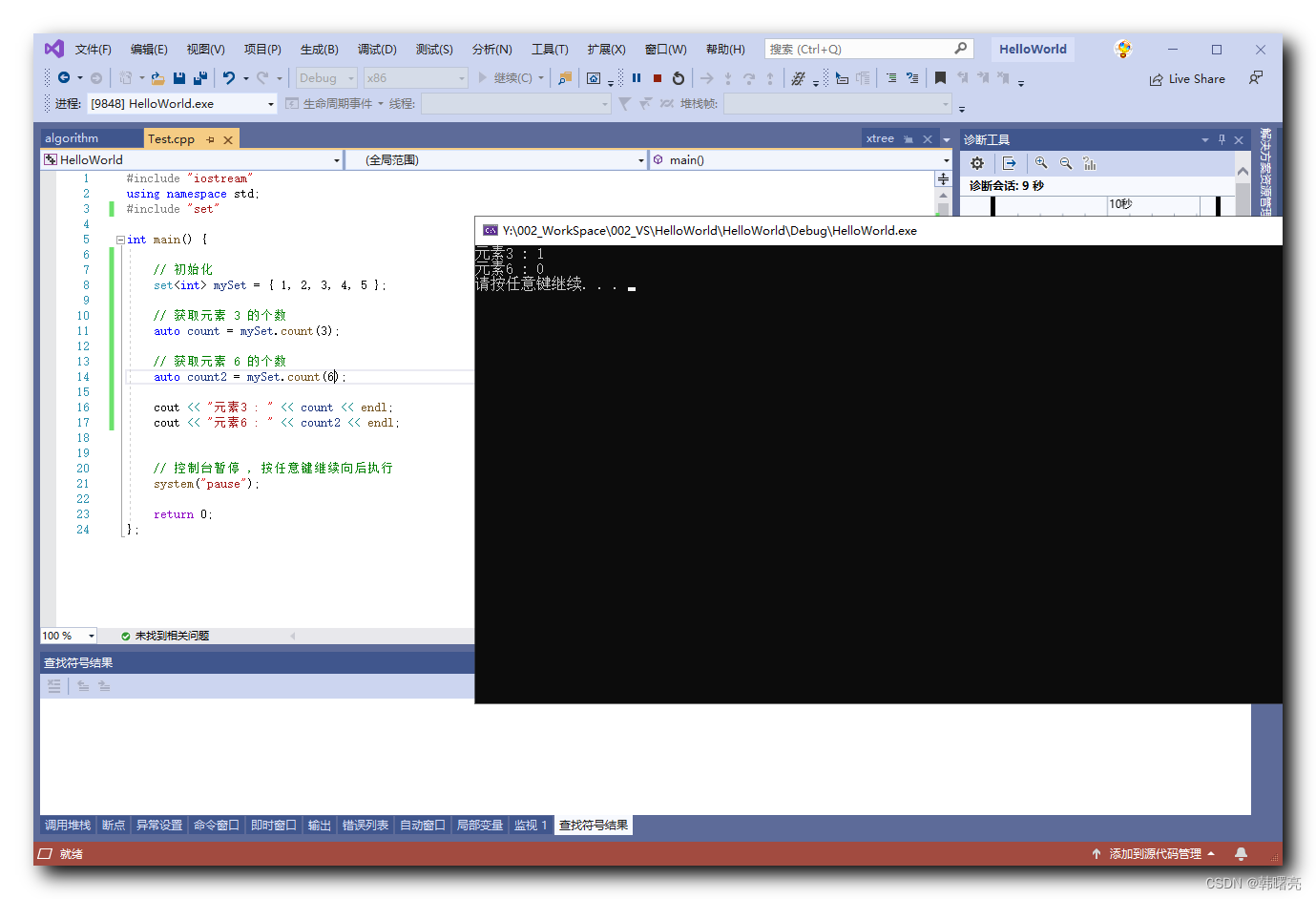
【C++】STL 容器 - set 集合容器 ⑦ ( 查找元素 - set#find 函数 | 获取元素个数 - set#count 函数 )
文章目录 一、查找元素 - set#find 函数1、函数原型 简介2、代码示例 - set#find 函数 二、获取元素个数 - set#count 函数1、函数原型 简介2、代码示例 - set#find 函数 一、查找元素 - set#find 函数 1、函数原型 简介 在 C 语言的 STL 标准模板库 , std::set 集合容器 是一个…
优化模型:matlab二次规划
1.二次规划
1.1 二次规划的定义
若某非线性规划的目标函数为自变量 x x x的二次函数,且约束条件全是线性的,则称这种规划模型为二次规划。
1.2 二次规划的数学模型 min 1 2 x T H x f T x \min \frac{1}{2}\boldsymbol{x}^{\boldsymbol{T}}\bolds…


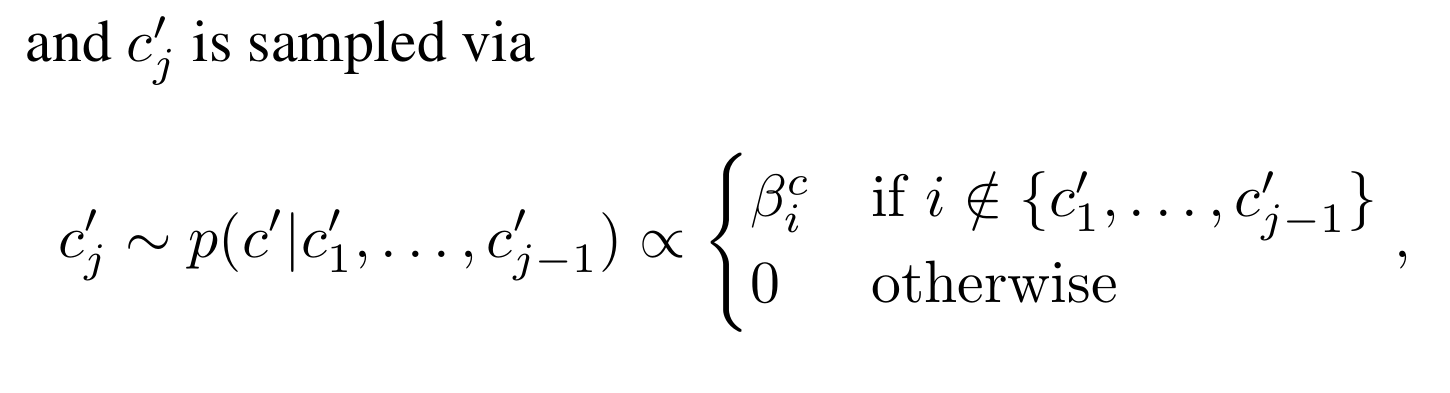


![[Angular] 笔记 20:NgContent](https://img-blog.csdnimg.cn/direct/87f629ff002d4a09b2e76c17f78fdf5c.png)


![[Angular] 笔记 24:ngContainer vs. ngTemplate vs. ngContent](https://img-blog.csdnimg.cn/direct/3140348447094532893519e0429d06ee.png)