随着人工智能技术的不断进步,现在可以通过拍摄照片结合AI技术来实现3D模型生成。这种技术的出现, 不仅能更加方便快捷地创建3D模型,而且还能真实复原现实中物件的质感、纹理等。同时,极大地降低了各行业对3D技术的应用门槛;
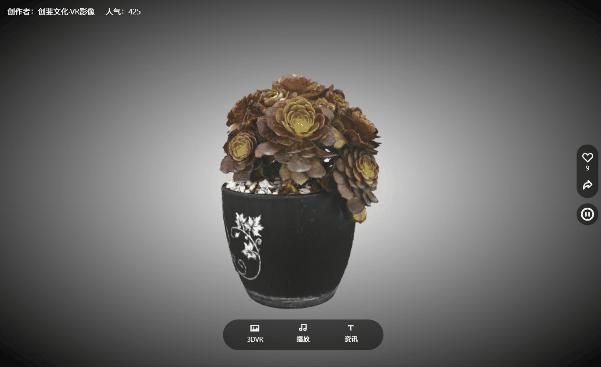
这种技术的实现原理主要是基于计算机视觉和深度学习等领域的技术。通过训练深度神经网络,让计算机能够自动识别照片中的三维结构,并根据这些结构信息生成出逼真的3D模型。同时,我们还可以通过优化算法和改进模型结构等方式,进一步提高3D模型的精度和逼真度。

传统3D建模往往需要专业技术和繁琐的步骤,然而,随着AI技术的飞速发展,我们现在可以通过深度学习等技术手段,让计算机自动从照片中提取出三维结构信息,从而快速生成高质量的3D模型。
这种技术的出现,带来了更多的创作可能性——数字孪生、建筑测量、文物保护等领域,为这些领域的工作提供更加精准的数据支持。

拍照3D建模技术正被越来越多的企业开始将这项技术应用于产品展示和宣传等领域,为消费者带来更加真实、生动的产品体验。

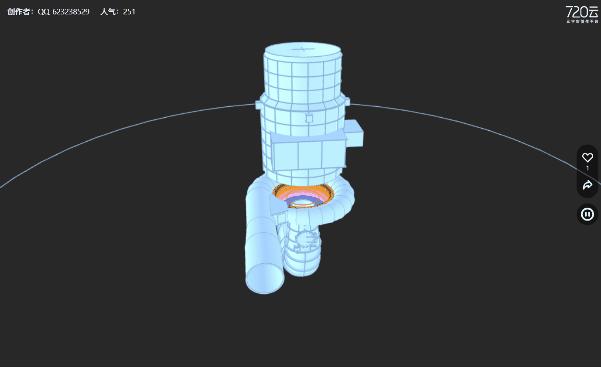
在产品宣传展示方面,拍照3D建模技术结合720云3D模型工具,可以将3D产品模型以高精度、高还原度的形式呈现在消费者面前。让消费者通过手机、电脑等浏览器就可以直观地了解产品的外观、结构、功能等特点。
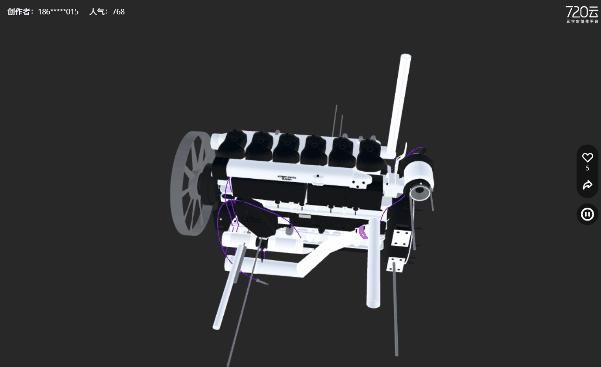
这对于一些复杂的产品来说尤为重要,比如机械设备、文物及其他实体化产品等,通过720云3D模型工具,消费者在手机上就可以,拖动、旋转、缩放的详细了解产品的细节和特点,提高购买决策的准确性。

通过将720云3D模型与社交媒体、广告、展览和游戏等领域相结合,可以创造出更具吸引力和互动性的内容,提高品牌知名度和用户参与度。

例如,在社交媒体上,可以通过720云3D模型生成的链接分享到平台上,吸引更多的关注和互动;在广告中,品牌可以利用这种技术制作出逼真的产品模型,提高广告的视觉效果和说服力;在展览中,这种技术可以为观众带来更加沉浸式的体验,让他们更加深入地了解展品和展览的主题。
总之,拍照720云3D模型作为一种新型的宣传手段,具有广泛的应用前景和发展潜力。通过与不同领域的结合,可以创造出更加丰富、生动和有趣的宣传内容,提高品牌知名度和用户参与度。然而,我们也需要关注技术的局限性和挑战,不断探索和完善拍照AI建模技术的应用方式和方法,以更好地服务于品牌和用户的需求。
![[Angular] 笔记 24:ngContainer vs. ngTemplate vs. ngContent](https://img-blog.csdnimg.cn/direct/3140348447094532893519e0429d06ee.png)