数字PID是由编程语言实现的PID算法并烧录到控制芯片中,控制芯片与电机驱动连接,将PID控制算法的输出转换为PWM控制信号发送给电机驱动电路,电机驱动电路与直流电机相连并将PWM控制信号转换为具有相同占空比的PWM供电电压,通过对输入电机的PWM供电电压占空比的控制实现对电机转速的调节;通过传感器监测电机转速,反馈至控制芯片,实现闭环。
1、公式推导
PID控制算法在连续时间序列下的公式如下:
![]()
对连续时间信号进行等间隔采样,就得到离散化的数字信号。

容易得到PID的离散化表达式,该表达式也成为位置式PID:

增量式PID,即ux - ux-1,表达式为:
![]()
所以,可以看出,位置式PID和增量式PID在本质上是同一种表达式。
2、PID控制的实际含义

以电机控制为例,期望转速是1000rpm,与实际电机转速(400rpm)的差值为600rpm输入PID控制器,电机驱动产生PWM波调节电机转速。

2.1、使用比例环节进行控制
只是用比例环节进行控制,e(t)为控制转速与电机实际转速的差值。

这是用比例环节进行电机控制的转速曲线,随着系数Kp的增加,转速曲线的波动越来越陡峭,波峰也越来越高。从Kp调节控制器的转速曲线可以发现,这里有两个问题:
1、存在转速波动。转速调节的初始阶段,电机转速有一段上下波动阶段(7秒前),这一段波动在实际应场景往往是不可以接受的;
2、存在稳态误差。在比例环节的控制下,电机的稳态转速始终与目标转存在偏差。根据比例环节的公式,当偏差消失后比例环节的输出也为0,因此稳态转速永远无法与目标转速一致。
实际中,随着Kp增加,前期转速波动增加、稳态误差降低,但始终无法消除。

2.2、增加微分环节
针对问题1的转速波动,可以通过增加微分环节来解决。

通过,下面的转速曲线,来看积分环节如何解决转速波动问题的。e(t)大于e(t-1)表示当前转速正在远离目标转速,根据积微分环节的公式,此时微分环节会将转速往靠近目标值进行调整。可以看到微分环节相当于一个阻尼器,转速原理目标值时,它阻止远离;转速靠近目标值时,它阻止靠近。从而让被控对象更快的稳定在一个状态,不进行波动。

2.3、增加积分环节
针对问题2的稳态误差问题,可以通过增加积分环节来解决。

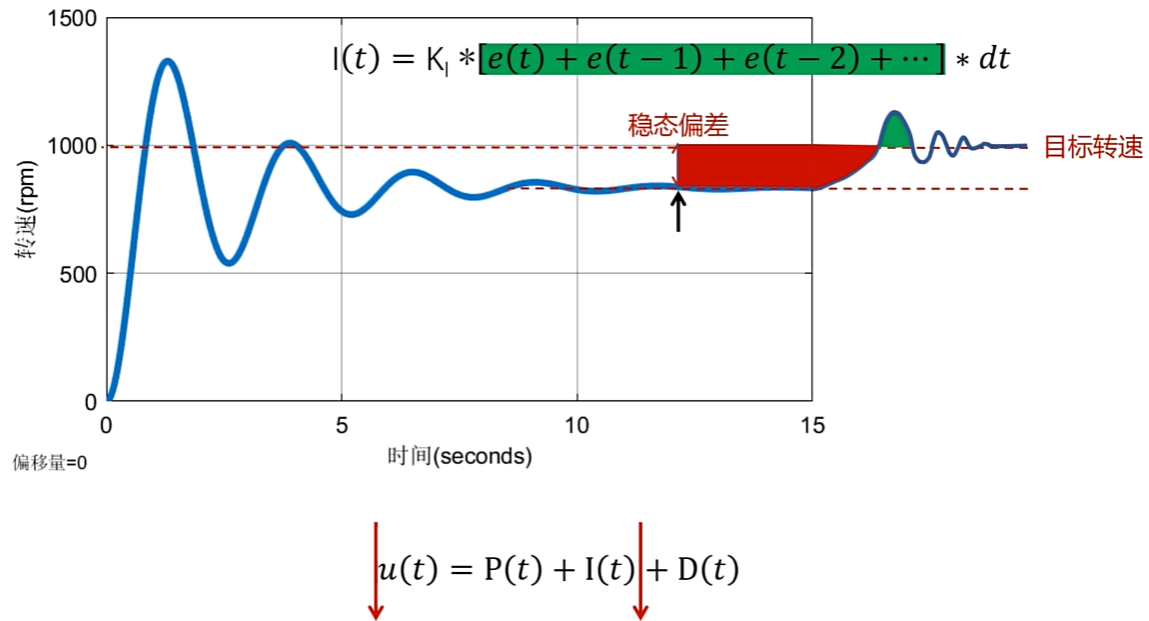
对于稳态误差,系统稳定后目标值和实际中始终存在一个偏差。如果此时,积分环节增加进来,它会对这部分偏差进行正向积分,在积分作用下,积分环节的输出变得越来越大,因此PID控制起的输出也变得越来越大,从而当前转速开始升高。当转速超过目标转速后,积分环节又会对这部分偏差进行负向积分,PID控制器的输出变小,从而转速开始下降。
只要转速没有停在目标转速上,积分环节就会一直发挥调节作用,被控对象会因为这种调节作用,最终稳定在目标转速上。
3、总结
PID控制器在只有比例环节时,存在转速波动和稳态误差。通过增加积分环节可以消除稳态误差,通过微分环节消除转速调节的波动问题。因此,在PID三个环节的共同努力下,就可以实现如下理想的转速调节曲线。



![[Angular] 笔记 20:NgContent](https://img-blog.csdnimg.cn/direct/87f629ff002d4a09b2e76c17f78fdf5c.png)


![[Angular] 笔记 24:ngContainer vs. ngTemplate vs. ngContent](https://img-blog.csdnimg.cn/direct/3140348447094532893519e0429d06ee.png)