1、设置问题
图片分类:只根据尺寸把它分类为 纵向图像和横向图像。

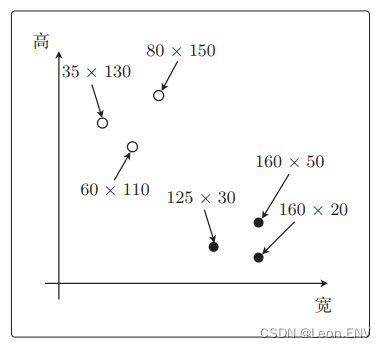
如果只用一条线将图中白色的点和黑色的点分开:

这次分类的目的就是找到这条线。
2、内积
找到一条线,这是否意味着我们要像学习回归时那样,求出一次函数的斜率和截距?
这个又不一样, 这次的目的是找出向量。
刚才画的那条线,是使权重向量成为法线向量的直线。
设权重 向量为 w,那么那条直线的表达式就是这样的:
![]()
实向量空间的内积是各相应元素乘积的和:
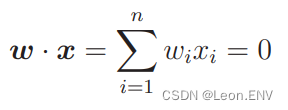
比如我们设权重向量为 w = (1, 1):

内积表达式表示的是这样的直线:
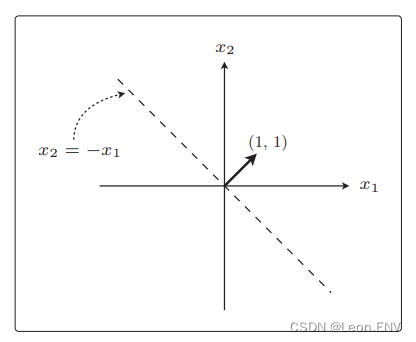
权重向量 w 和这条直线是垂直的, 这就是“使权重向量成为法线向量的直线”在图形上的解释。
用向量之间的夹角 θ 和 cos 计算内积的表达式:
![]()
这是内积的另一个表达式。用这个表达式也没有问题。
表达式中 的 |w| 和 |x| 是向量的长,因此必定是正数。
所以要想使内积为 0,只能使 cos θ = 0。
要想使 cos θ = 0,也就意味着 θ = 90◦ 或 θ = 270◦ ,这两种情况也是直角。
最终找到与上面画的直线成直角的权重向量就行了:

当然,一开始并不存在这条直线,而是要通过训练找到权重向量,然后才能得到与这个向量垂直的直线,最后根据这条直线就可以对数据进行分类了。
3、感知机
具体要如何求出权重向量?
基本做法和回归时相同:将权重向量用作参数,创建更新表达式来 更新参数。接下来,要说明的就是被称为感知机(perceptron) 的模型。
感知机是接受多个输入后将每个值与 各自的权重相乘,最后输出总和的模型:
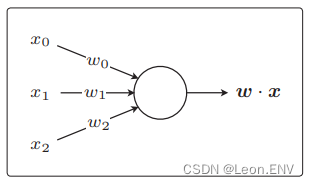
感知机是非常简单的模型,基本不会应用在实际的问题中, 但它是神经网络和深度学习的基础模型。
训练数据的准备
设表示宽的轴为 x1、表示高的轴为 x2,用 y 来 表示图像是横向还是纵向的,横向的值为 1、纵向的值为 −1。
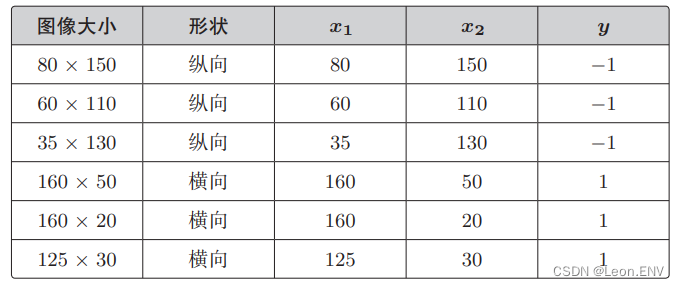
判别函数:

这是根据内积的符号(正或负)来给出不同返回值的函数。
如: 与权重向量 w 的内积为负的向量 x 是 什么样的向量?
![]()
|w| 和 |x| 必定为正数,所以决定 内积符号的是 cos θ:

在 90◦ <θ< 270◦ 的时候 cos θ 为负。
所以与权重向量 w 之间的夹角为 θ,在 90◦ <θ< 270◦ 范围内的所有向量都符合条件:
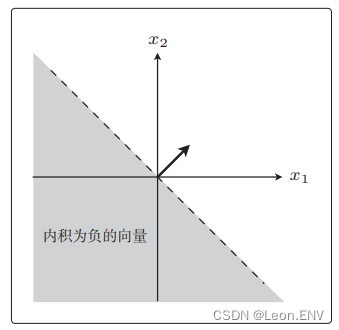
同样使内积为正的向量:
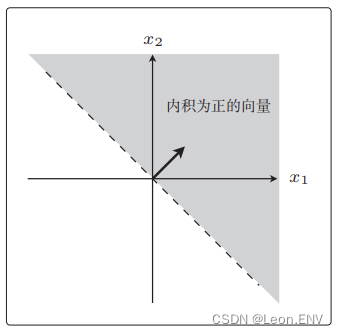
这样就 可以根据内积的正负来分割。
内积是衡量向量之间相似程度的指标。结果为正,说明二者相似; 为 0 则二者垂直;为负则说明二者不相似。
权重向量的更新表达式
样定义权重向量的更新表达式:

更新表达式只有在判别函数分类失败的时候 才会更新参数值。
如: 现在权重向量 w 和训练数据的向量 x(1) 二者的方向几乎相 反,w 和 x(1) 之间的夹角 θ 的范围是 90◦ <θ< 270◦ ,内积为负, 判别函数 fw(x(1)) 的分类结果为 −1,实际 y(1) 为 1。
说明分类失败,需要更新权重:
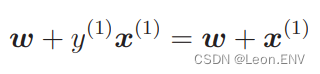
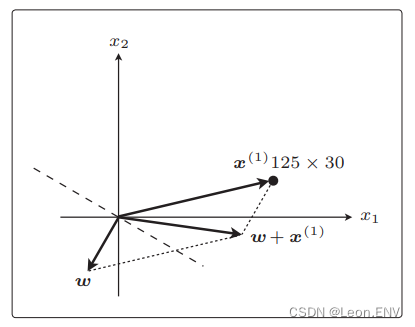
刚才x(1) 与权重向量分居直线两侧,现在它们在同 一侧。
刚才处理的是标签值 y = 1 的情况,而对于 y = −1 的情况,只是 更新表达式的向量加法变成了减法而已,做的事情是一样的。
虽然有加法和减法的区别,但它们的做法都是在分类失败时更新权重向量,使得直线旋转相应的角度。
4、线性可分
感知机非常简单又容易理解,但相应地,缺点也有很多。
最大的缺点就是它只能解决线性可分的问题。
之前提到的感知机也被称为简单感知机或单层感知机,真的是很弱的模型。不过,既然有单层感知机,那么就会有多层感 知机。实际上多层感知机就是神经网络了。
5、逻辑回归
逻辑回归与感知机的方法不一样。
逻辑回归与感知机的不同之处在于,它是把分类作为概率来考虑的。
这里设横向的值为 1、纵向的值为 0。这个也和感知机的时候不一样了,纵向不是 −1 了。
只要是两个不同的值,用什么都可以。在学习感知机时之所以设 置值为 1 和 −1,是因为这样会使参数更新表达式看起来更简洁, 而现在则是设置为 1 和 0 会更简洁。
sigmoid 函数
学习回归时定义过这样一个带参数 的函数:
![]()
我们需要能够将未知数据分类为某个类别的函数 fθ(x):

这个函数的名字叫 sigmoid 函数,设 θTx 为横轴,fθ(x) 为纵轴:

θTx = 0 时 fθ(x)=0.5,以及 0 < fθ(x) < 1 是 sigmoid 函数的两 个特征。
因为 sigmoid 函数的取值范围是 0 < fθ(x) < 1,所以它可以作为概率来使用。
决策边界
把未知数据 x 是横向图像的概率作为 fθ(x):
![]()
这是在给出 x 数据时 y = 1,即图像为横向的概率。
应该是以 0.5 为阈值,然后根据 fθ(x) 的结果分类横向或纵向:

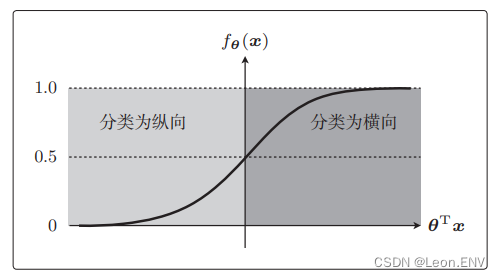
所以我们可以把上面的表达式改写:
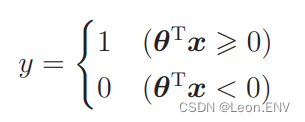
下面像学习感知机时那样,设横轴为图像的宽(x1)、纵轴为图像的高(x2),并且画出图来考虑。
然后像学习回归时那样,先随便确定 θ 再具体地去考虑。
比如当 θ 是这样的向量时,我们来画一下 θTx ⩾ 0 的图像:
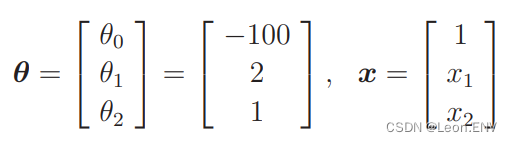
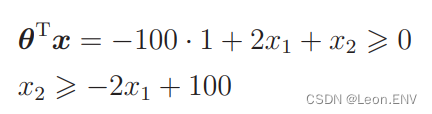
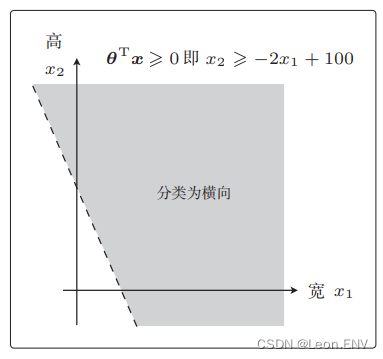
这个不等式表示的范围也就是图像被分类为横向的范围了:
为纵向的范围:
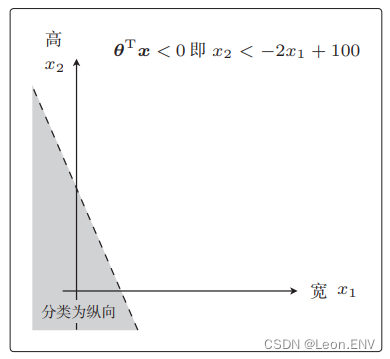
也就是说,将 θTx = 0 这条直线作为边界线,就可以把这条线两侧的数据分类为横向和纵向了。
这样用于数据分类的直线称为决策边界。
实际应用时这个决策边界似乎不能正确地分类图像,这是因为我们决定参数时太随意了:

为了求得正确的参数 θ 而定义目标函数,进行微分,然后求参数的更新表达式。
这种算法就称为逻辑回归。
6、 似然函数
训练数据的标签 y 和 fθ(x)是什么样的关系会比较理想:
● y = 1 的时候,我们希望概率 P(y = 1|x) 是最大的
● y = 0 的时候,我们希望概率 P(y = 0|x) 是最大的
这适用于全部的训练数据。对于一开始列举的那 6 个训练数据,我们期待的最大概率是这样
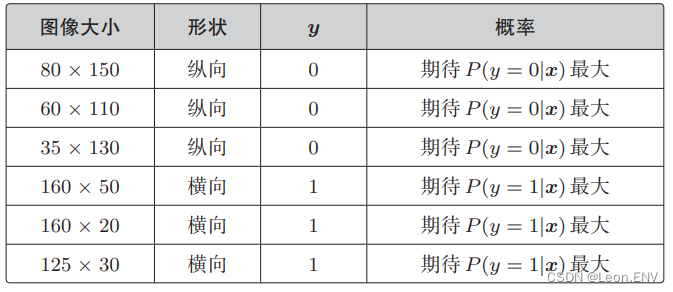
假定所有的训练数据都是互不影响、独立发生的,这种情况下整体的概率就可以用下面的联合概率来表示(同时发生的概率):
![]()
且联合概率的表达式是可以一般化的,写法如下:

(该联合乘法符号读作“派”)
接下来考虑一下使这个目标函数最大化的参数 θ。
回归的时候处理的是误差,所以要最小化,而现在考虑的是联合概率,我们希望概率尽可能大,所以要最大化。
这里的目标函数 L(θ) 也被称为似然,函数的名字 L 取自似 然的英文单词 Likelihood 的首字母。
它的意思是最近似的。我们可以认为似然函数 L(θ) 中,使其值最大的参数 θ 能够最近似地说明训练数据。
7、对数似然函数
直接对似然函数进行微分有点困难,在此之前要把函数变形。
首先它是联合概率。概率都是 1 以下的数,所以像联合概率这种 概率乘法的值会越来越小。
如果值太小,编程时会出现精度问题。另外还有一个,那就是乘法与加法相比,乘法的计算量要大得多。
解决方法:
只要取似然函数的对数就好了,像这样在等式两边加上 log 即可:

回归的时候是随便乘了个常数(1/2),这次随便取对数也没问题吗?
没问题的,因为 log 是单调递增函数:
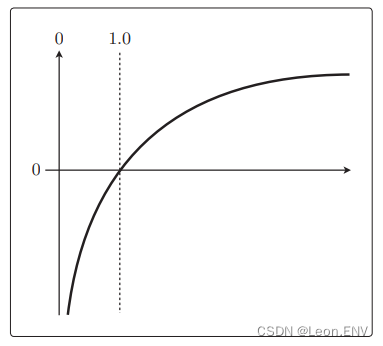
单调递增函数是在 x1 < x2 时, f(x1) < f(x2) 的函数 f(x)。
现在考察的似然函数也是在 L(θ1) < L(θ2) 时,有 logL(θ1) < logL(θ2) 成立。
也就是说,使 L(θ) 最大化等价于使 logL(θ) 最大化。
把对数似然函数变形:
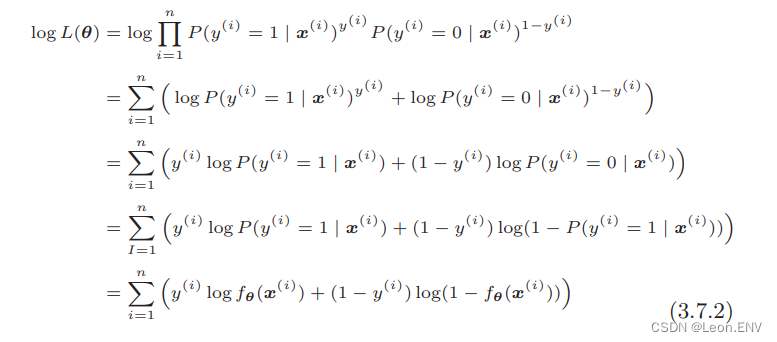
每一行的变形分别利用了下面这些特性:
● 第 2 行是 log(ab) = log a + log b
● 第 3 行是 log ab = b log a
● 第 4 行是 P(y(i) = 0|x(i) ) = 1 − P(y(i) = 1|x(i) )
似然函数的微分
总结一下就是逻辑回归将这个对数似然函数用作目标函数:
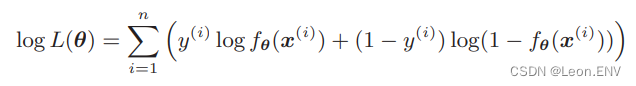
接下来对各个参数 θj 求微分:

把似然函数也换成这样的复合函数, 然后依次求微分:

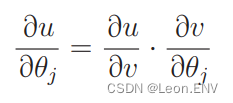

log(v) 的微分是 1/v 。
不过对 log(1 − v) 微分时,要像这样通过复合函数来求。还要注意,这样做最后的表达式前面会有个负号:

微分结果是:
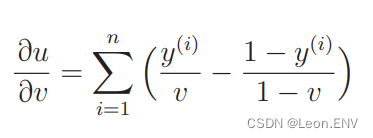
接下来是 v 对 θj 的微分:
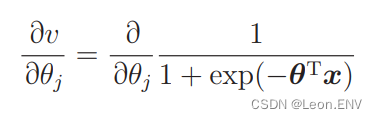
sigmoid 函数的 微分是这样的:

求解:
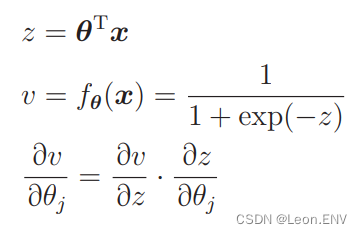
v 对 z 微分:
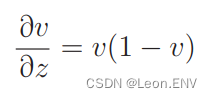
z 对 θj 的微分:
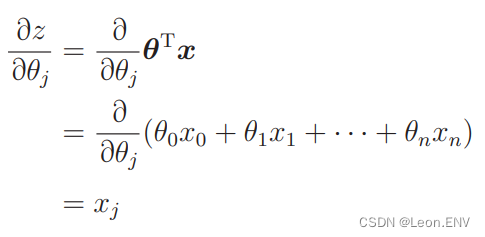
得出:
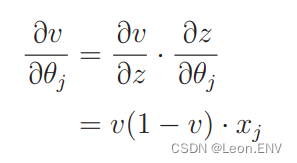
最后代入各个结果:
接下来要做的就是从这个表达式导出参数更新表达式。
不过现在是以最大化为目标,所以必须按照与最小化时相反的方向移动参数。
也就是说,最小化时要按照与微分结果的符号相反的方向移动,而最大化时要与微分结果的符号同向移动:

为了与回归时的符号保持一致,也可以将表达式调整为下面这样:
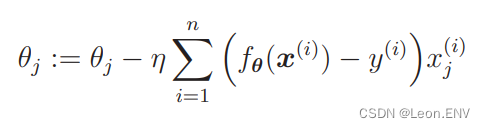
注意,η 之前的符号和 ∑中的符号反转了。
8、 线性不可分
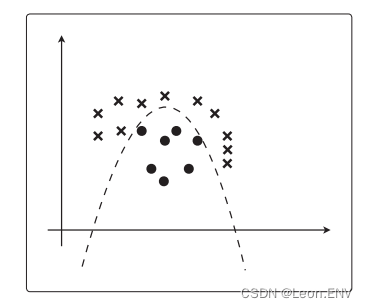
最后,我们将逻辑回归应用于线性不可分问题。
我们可以像学习多项式回归时那样,去增加次数, 向训练数据中加入 x1^2 :

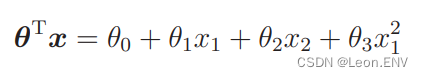
假设 θ 是这样的向量,那么 θTx ⩾ 0 的图形是什么样的?
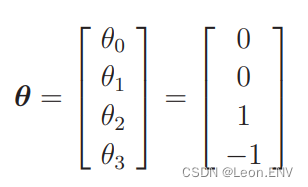
先代入:
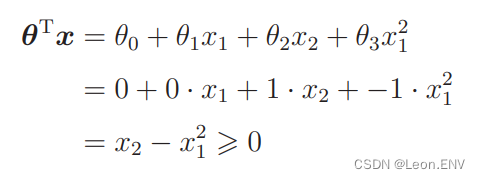
移项后最终得到的表达式是 x2 ⩾ x1^2 ,将这个画成图:
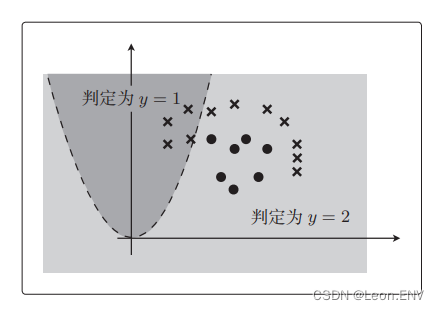
之前的决策边界是直线,现在则是曲线了。
参数 θ 是随便定的,所以数据完全没有被正确地分类。
之后通过随意地增加次数,就可以得到复杂形状的决策边界了。 比如在 x1^2 之外再增加一个 x2^2,就会有圆形的决策边界。
在逻辑回归的参数更新中也可以使用随机梯度下降法。