🌈个人主页: Aileen_0v0
🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法
💫个人格言:"没有罗马,那就自己创造罗马~"

---

目录

冒泡排序

过程演示：

冒泡排序实现代码：

分析冒泡排序：

Practice1：

📝总结： 

---

冒泡排序

过程演示：

 

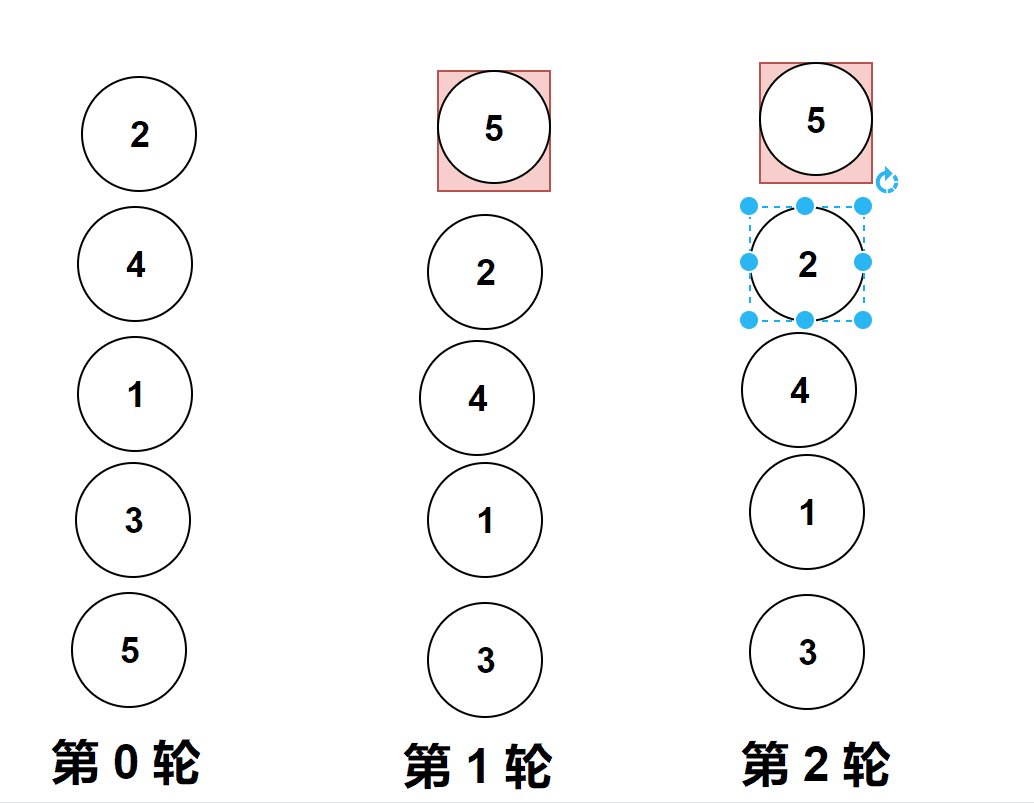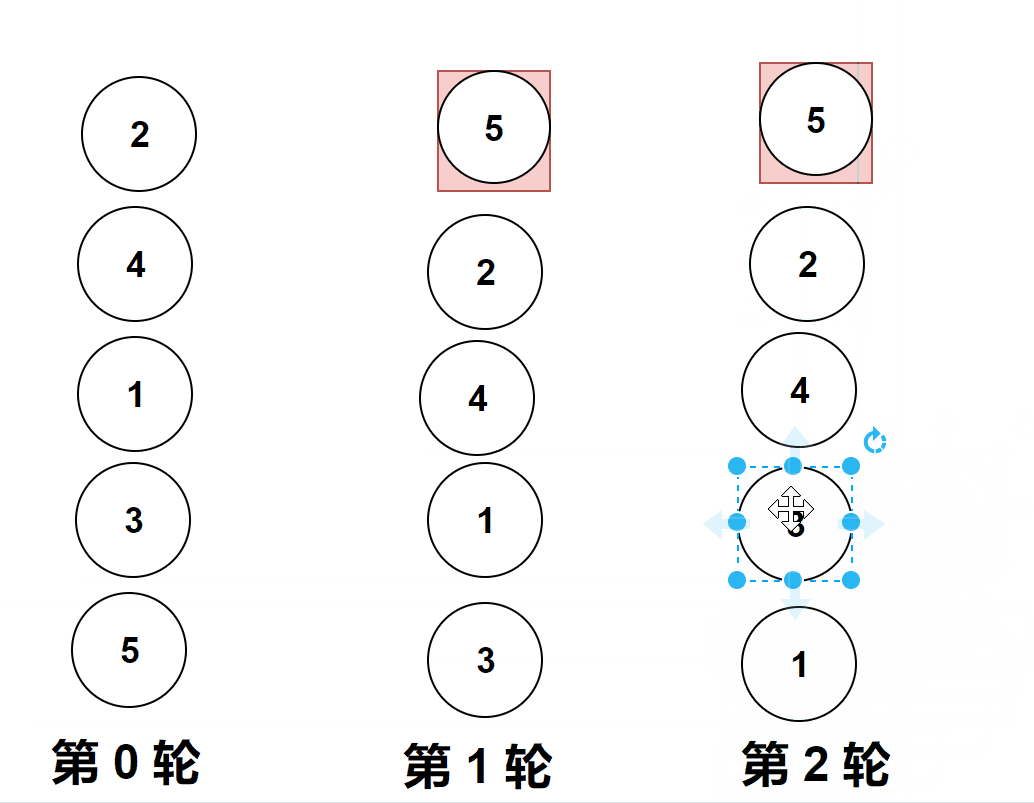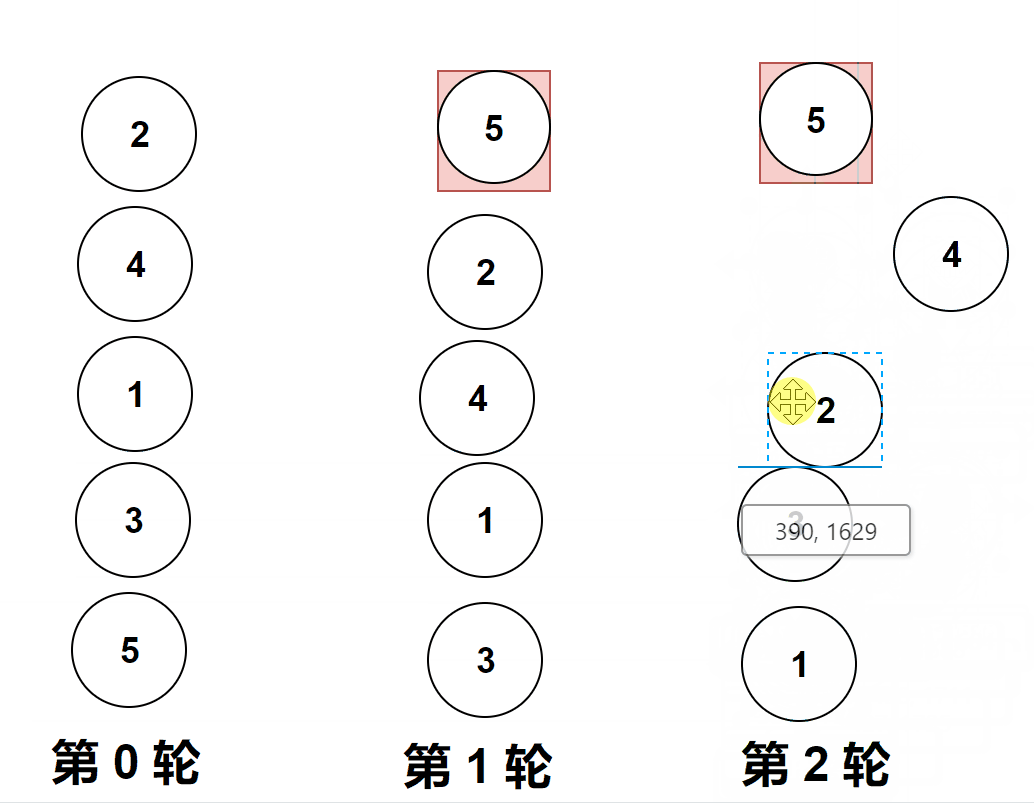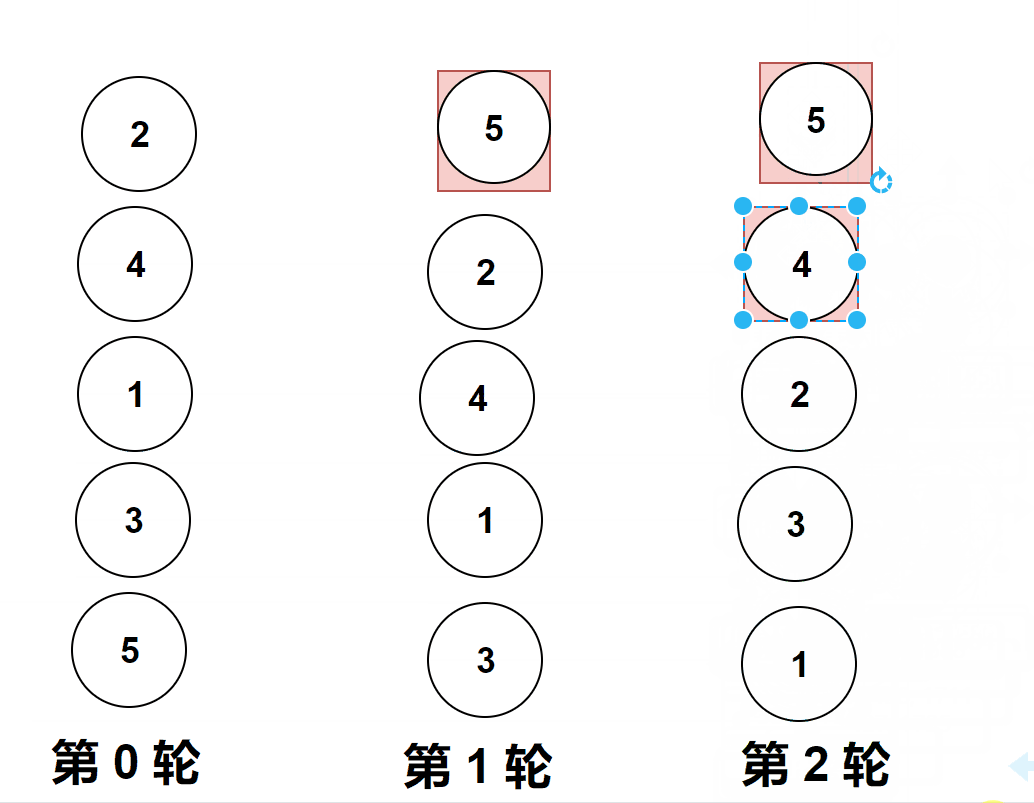
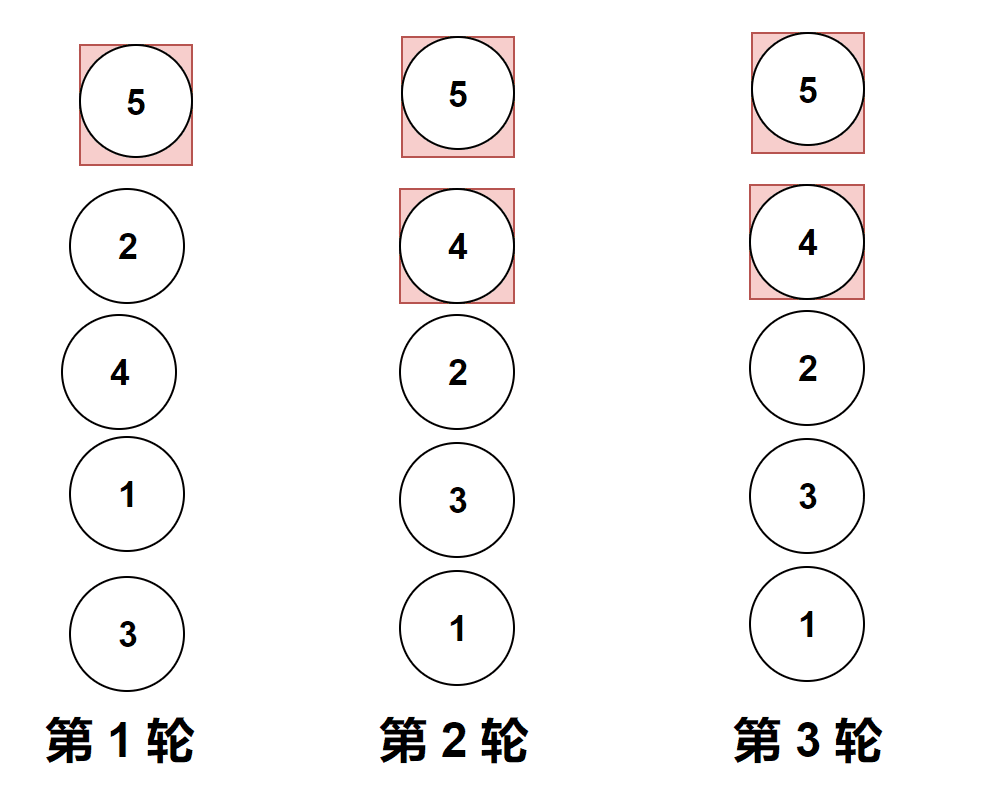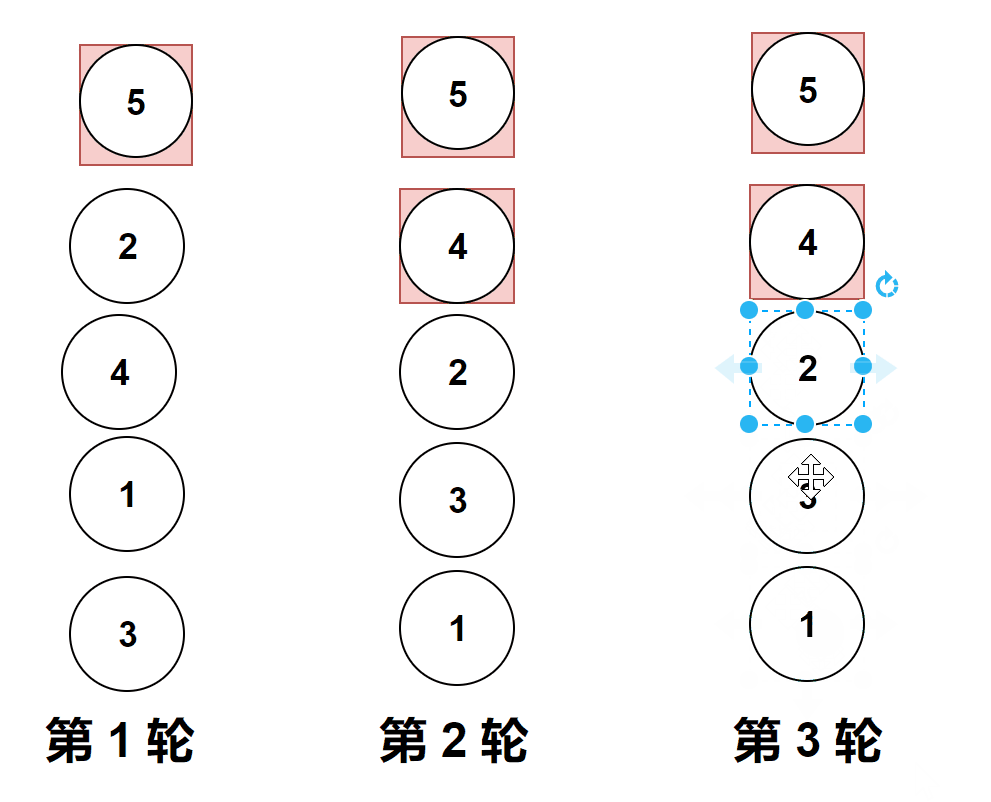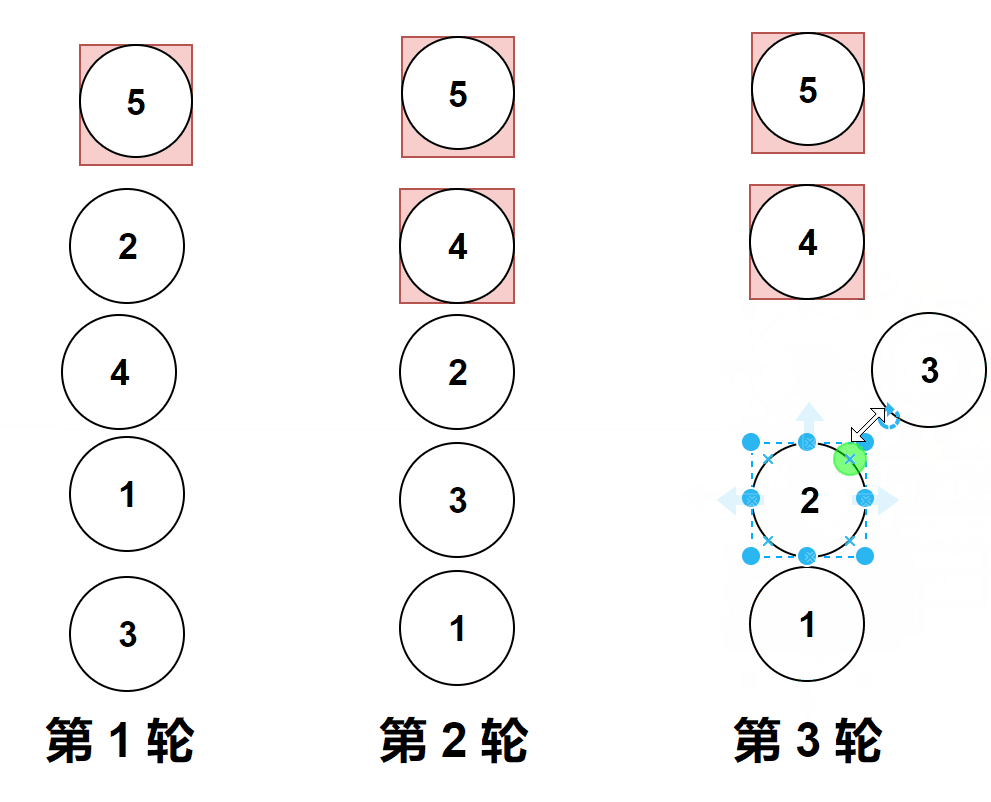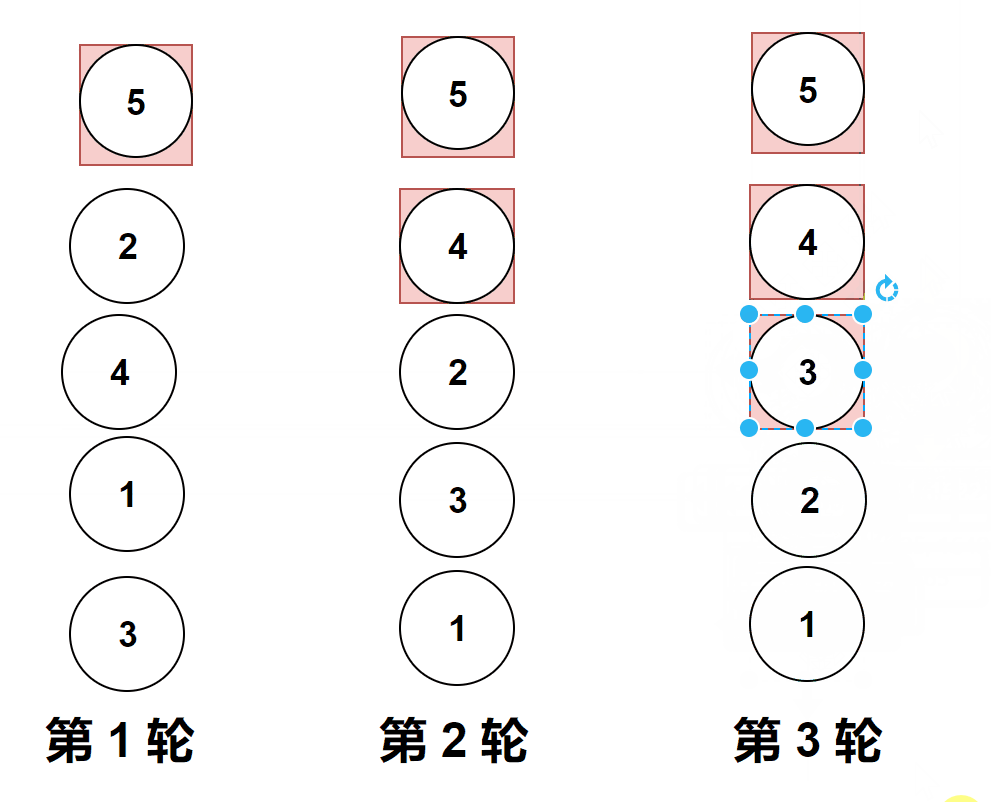
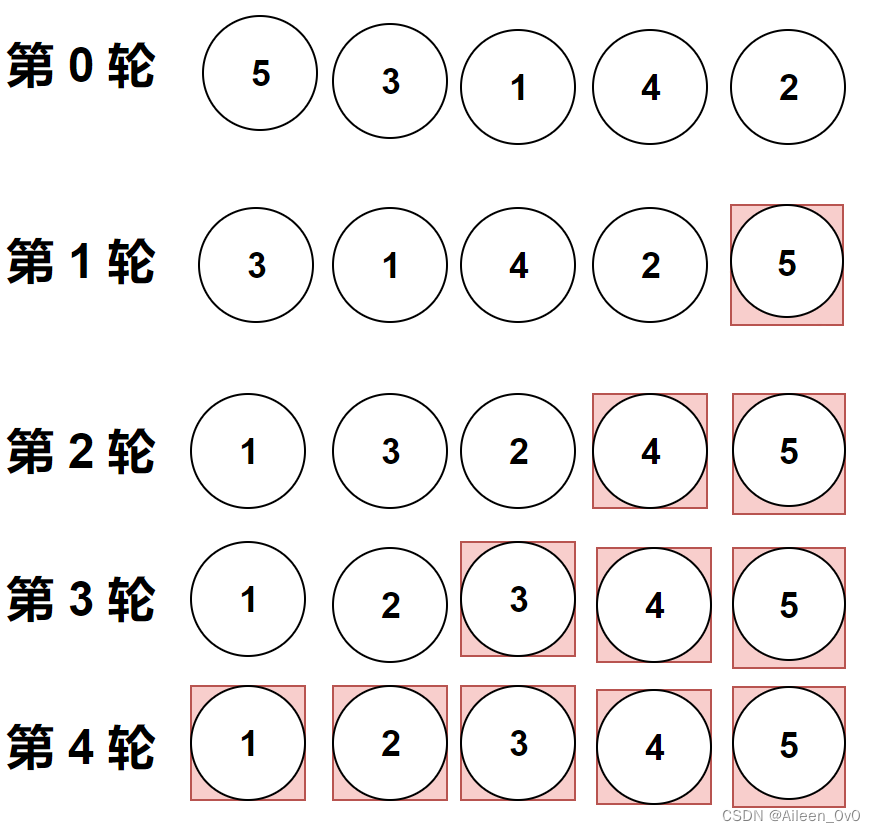
做题实际遇到的图像是横向的，但是它位置变化和纵向是一样的，上面的gif图是为了让大家更加直观的看清楚冒泡排序。

比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。

这步做完后，最后的元素会是最大的数。

针对所有的元素重复以上的步骤，除了最后一个。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

插入排序是连续对比，而冒泡排序是挨个对比

第1趟比较交换，【共有n-1】  即如图中的4对相邻数据进行比较，一旦经过最大项，则最大项会一路交换到达最后
一项
第2趟比较交换时，最大项已经就位，需要排序的数据减少为n-1，共有n-2对相邻数据进行比较
直到第n-1趟完成后，最小项一定在列表首位，就无需再处理了。

冒泡排序实现代码：

def bubble_sort(q):
    #循环遍历（起泡）次数
    for i in range(0,len(q)):
        #每次起泡里比对的次数
        for j in range(0,len(q) - i - 1 ):
            #当前位置的值大于下一个位置的值
            if q[j] > q[j + 1]:
                q[j] , q[j + 1] = q[j + 1] , q[j]
    return q

list = [1,5,33,88,44,77,99,0,66]
print(bubble_sort(list))

分析冒泡排序：

分析冒泡排序算法时要注意，不管一开始元素是如何排列的，给含有n个元素的列表排序总需要遍历 n-1轮。

下表展示了每一轮的比较次数。

总的比较次数是前 n-1个整数之和。即： (1 / 2)n² + （1 / 2)n ,可以看出这个算法的时间复杂度是 O(n²)。

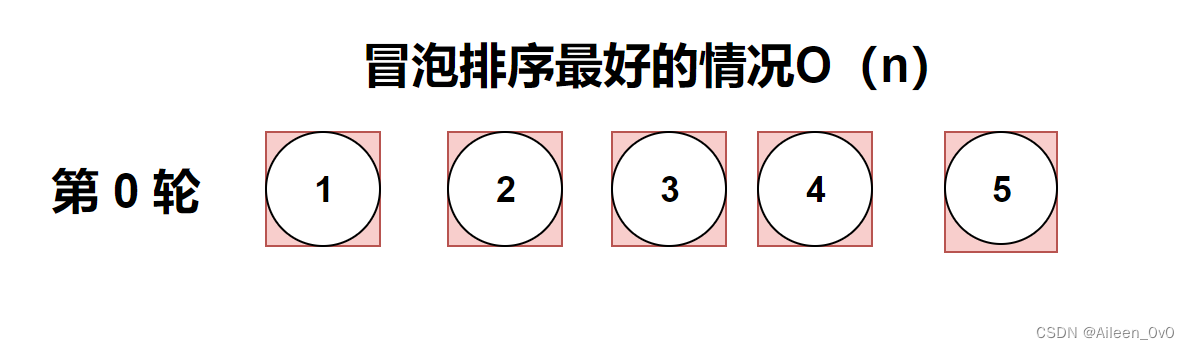
在最好情况下，列表已经是有序的，不需要执行交换操作。

在最坏情况下，每一次比较都将导致一次交换。 

劣势：冒泡排序通常作为时间效率较差的排序算法，来作为其它算法的对比基准，其效率主要差在每个数据项在找到其最终位置之前必须要经过多次比对和交换，其中大部分的操作是无效的。
优势：就是无需任何额外的存储空间开销。

Practice1：

 抓住冒泡排序的特点，最大的往后排，所以选B。

📝总结：