关键词：动态规划 最长公共子序列

题目：

思路：

这题我虽然做出来了但是还是有点迷糊。首先，这道题一定是和最长公共子序列相似的。

所以往最长公共子序列方向思考，考虑的它的状态和转移方程以及边界。

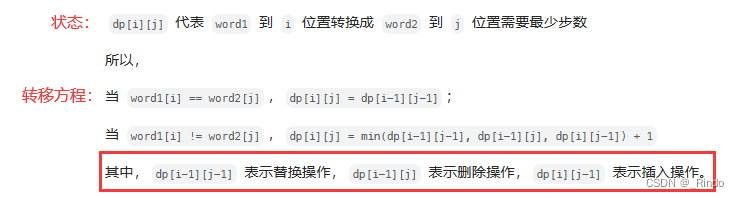
状态和转移方程：

这里的替换 删除 插入需要好好琢磨一下。可以结合实际例子理解。

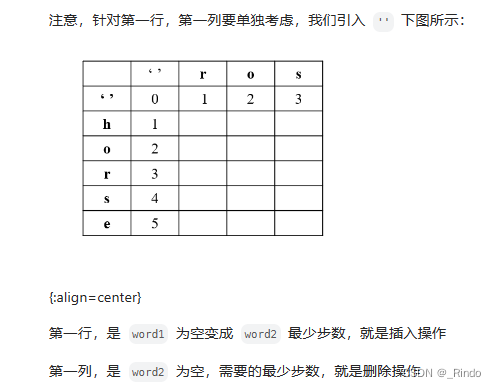
边界：

（第一次提交的时候没有注意，刚开始把边界都设成了intmax）

复杂度计算：

时间复杂度O(nm)

空间复杂度O(nm)

代码：

class Solution {
public:
    int minDistance(std::string word1, std::string word2) {
        if (word1.empty() || word2.empty()) //两个string里面至少有一个是空的
            return word1.length() + word2.length();
        //两个string都不空
        int n = word1.length() + 1;
        int m = word2.length() + 1;
        std::vector<std::vector<int>> dp(m, std::vector<int>(n, 0));
        //边界
        for (int i = 0; i < dp[0].size(); ++i)
            dp[0][i] = i;
        for (int i = 0; i < dp.size(); ++i)
            dp[i][0] = i;
        //遍历每一个
        for (int i = 0; i < word2.length(); ++i)
        {
            for (int j = 0; j < word1.length(); ++j)
            {
                if (word1[j] == word2[i])
                    dp[i + 1][j + 1] = dp[i][j];
                else
                    dp[i + 1][j + 1] = std::min(std::min(dp[i][j], dp[i][j + 1]), dp[i + 1][j]) + 1;
            }
        }
        return dp[word2.length()][word1.length()];
    }
};