区间DP详解，思路分析，OJ详解

文章目录

- 前言
- 问题引入
- - 暴力枚举
  - 自下而上
  - 状态设计
  - 状态转移方程
- 区间DP的分析
- - 状态设计
  - 状态转移
  - 时间复杂度
  - 翻译成递推
- OJ详解
- - P1880 [NOI1995] 石子合并
  - - 记忆化搜索版本
    - 递推版本
  - HDU Dire Wolf
  - Multiplication Puzzle
  - Polygon
- 总结

前言

区间dp属于动态规划中一类比较好理解的问题，同样是将大问题分划成小问题来求解。主要要理解其对区间问题拆解的思想，掌握状态转移的处理细节，通过对区间dp的学习，也能更好的理解自底向上分析问题的思想。

问题引入

在一个圆形操场的四周摆放N堆石子，第i堆石子的重量为w[i]，现要将石子有次序地合并成一堆，规定每次只能选相邻的2堆合并成新的一堆，并将新的一堆的石子重量，记为该次合并的代价。试设计出一个算法，计算出将N堆石子合并成1堆的最小代价。

在对区间dp没有了解的情况下，本蒟蒻解题过程很可能是这样的：

看题 -> 贪心？-> 代码一气呵成 -> WA -> 选择暴力 -> TLE -> 看题解 -> 区间DP？什么东西？-> orz

那么我们从暴力解法开始入手，寻找优化之处。

暴力枚举

即然要将n堆石子合并成一堆，我们自然要合并n - 1次，对于我们第一次合并，两两相邻的情况有n - 1种，那么第一次合并就有n - 1种情况

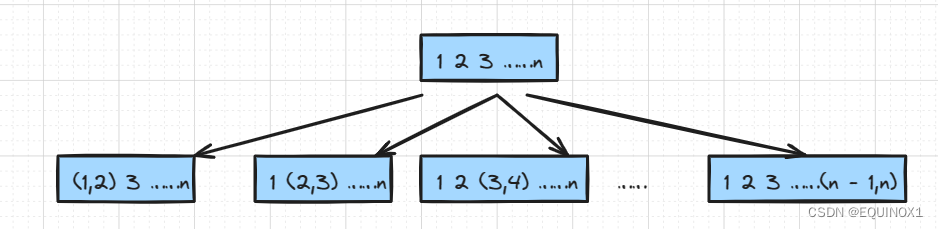
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

那么n - 1种情况继续向下分支，每种情况又能分出n - 2种情况

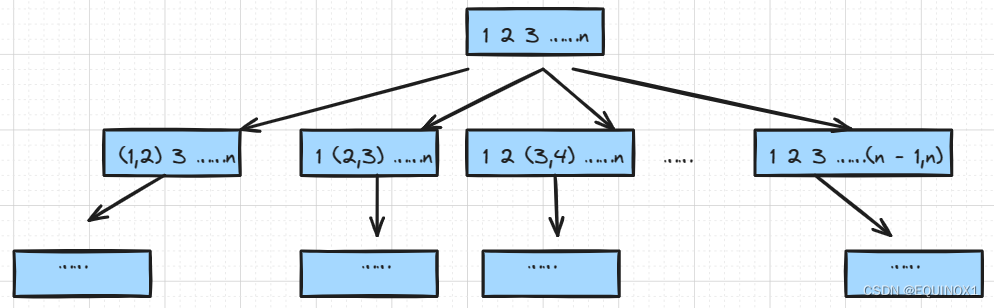
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

从而我们得到了一棵非常庞大的搜索树，每条从根节点到叶子节点的路径为一个方案，一共有(n - 1)!种方案，暴力算法显然会超时，那么我们如何去优化呢？

自下而上

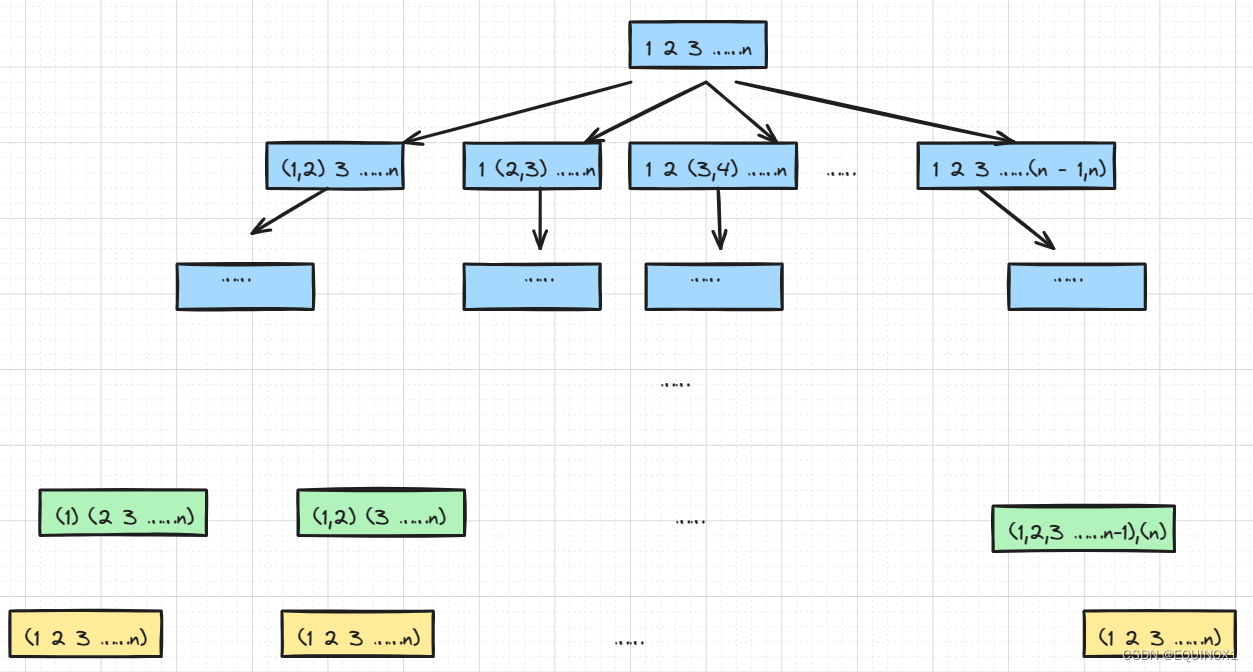
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

我们观察那棵庞大的搜索树，我们发现最后一层叶子节点相同都是一堆石子，倒数第二层是两堆石子，

我们发现对于倒数第二层而言，它们合并的花费是相同的，都是两堆石子重量之和——所有的石子重量之和，我们设倒数第二层的情况为合并(1……k)和(k+1……n)，那么我们如果要最小花费，那么只需要合并(1……k)和(k+1……n)都达到最小花费即可，这样我们的问题就分划为了合并(1……k)和(k+1……n)的最小花费

同样的，(1……k)和(k+1……n)又可以分割成更小的区间，最终区间会不断缩小，会变成合并1个石子的最小花费，即0，因为一个石子不需要合并。

我们发现，此时问题就可以抽象为动态规划的模型了。

状态设计

设计状态f[l][r]为合并第l堆石子一直到第r堆石子的最小代价。

状态转移方程

$\left\{\begin{align} &0&l=r\\ &min_{i=l}^{r-1}(f[l][i] + f[i + 1][r] + sum(l,r))&l \ne r \end{align}\right. \\ sum(l,r) = \sum_{j = l}^{r}w[j]$

通过对递归树的分析观察，这个状态转移方程其实不难理解。

l = r，那么已经是一堆了，合并代价为0
l ≠ r，那么对于倒数第二次合并一定是由两堆合并，由r - l种情况，一堆为(l , i)，另一堆为(i + 1, r)，两堆合并为一堆的代价sum(l,r)是确定的，只需要f[l][i] + f[i + 1][r]最小即可。

我们通过深搜计算答案，但是会有大量重复走的递归树路径，所以采用记忆化搜索进行剪枝，这样我们的时间复杂度就大大提升。

以上就是最经典的区间dp问题。

区间DP的分析

状态设计

区间DP的状态与区间有关，一般为二维数组f[i][j]来表示问题在区间[i , j]的解

对于一些变形问题，需要额外空间来辅助求解时，也会将空间扩展为三维，即f[i][j][k]，这也是动态规划问题中常见的辅助手段

状态转移

长区间问题的解由小区间问题的解转移过来

时间复杂度

以引例为例，区间长度为n，状态数为n^{2，每个状态只计算了一次，每次O(n)转移，那么时间复杂度为O(n}3)

具体的时间复杂度具体问题具体分析。

翻译成递推

对于记忆化搜索的做法其实是把顶层问题拆分为了下层问题，下层问题先计算，传递到上层

那么我们也可以直接从下层开始计算，每次由前面计算过的值转移即可，这样就把递归问题翻译成了递推问题，省去了递归开销。

具体实现可以自行实现，也可以看后面第一道OJ详解中的实现。

OJ详解

P1880 [NOI1995] 石子合并

原题链接

[P1880 NOI1995] 石子合并 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

这其实就是我们问题引入的问题，只不过要求我们同时计算出最大值和最小值，解法显然相同，只是初始化不同罢了

对于求最大值的，我们就把f[][]初始化为0，非0的状态就是访问过的，直接返回，l = r直接返回0，否则就进行状态转移

对于求最小值，我们就把f[][]初始化为无穷大的数(记为inf)，对于不是inf的，说明访问过，直接返回，l = r直接返回0，否则就进行状态转移

小细节：由于石子是环形放置，这里采用无脑将数组倍增一倍，破环成链。那么最终的答案还需要枚举长度为n的区间中的最值

记忆化搜索版本

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <unordered_set>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 220
int a[N]{0}, f1[N][N], f2[N][N]{0}, n;
const int inf = 0x3f3f3f3f;
int dfs1(int l, int r)
{
    if (f1[l][r] != inf)
        return f1[l][r];
    if (l == r)
        return f1[l][r] = 0;

    int &dp = f1[l][r];
    for (int k = l; k < r; k++)
        dp = min(dp, dfs1(l, k) + dfs1(k + 1, r) + a[r] - a[l - 1]);
    return dp;
}
int dfs2(int l, int r)
{
    if (f2[l][r])
        return f2[l][r];
    if (l == r)
        return f2[l][r] = 0;

    int &dp = f2[l][r];
    for (int k = l; k < r; k++)
        dp = max(dp, dfs2(l, k) + dfs2(k + 1, r) + a[r] - a[l - 1]);
    return dp;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    memset(f1, 0x3f, sizeof(f1));
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i], a[i + n] = a[i];
    for (int i = 1; i <= n * 2; i++)
        a[i] += a[i - 1];
    dfs1(1, n * 2);
    dfs2(1, n * 2);
    int ans1 = 0x3f3f3f3f, ans2 = 0;
    for (int i = 1; i < n; i++)
        ans1 = min(ans1, f1[i][i + n - 1]), ans2 = max(ans2, f2[i][i + n - 1]);
    cout << ans1 << '\n'
         << ans2;
    return 0;
}

递推版本

#include <iostream>
#include <cstring>
#include <vector>
#include <functional>
#include <algorithm>
#include <cmath>
#include <functional>
#include <climits>
#include <unordered_set>
#include <bitset>
#include <stack>
#include <cstring>
using namespace std;
#define N 220
int a[N]{0}, f1[N][N], f2[N][N]{0}, n;
const int inf = 0x3f3f3f3f;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    memset(f1, 0x3f, sizeof(f1));
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i], a[i + n] = a[i], f1[i][i] = f1[i + n][i + n] = f2[i][i] = f2[i + n][i + n] = 0;
    for (int i = 1; i <= n * 2; i++)
        a[i] += a[i - 1];

    for (int i = 2; i <= n; i++) // 枚举长度
    {
        for (int j = 1; j <= n * 2 - i + 1; j++) // 枚举区间起点
        {
            for (int k = j; k < j + i - 1; k++) // 枚举左子区间右边界
            {
                f1[j][j + i - 1] = min(f1[j][j + i - 1], f1[j][k] + f1[k + 1][j + i - 1] + a[j + i - 1] - a[j - 1]);
                f2[j][j + i - 1] = max(f2[j][j + i - 1], f2[j][k] + f2[k + 1][j + i - 1] + a[j + i - 1] - a[j - 1]);
            }
        }
    }

    int ans1 = 0x3f3f3f3f, ans2 = 0;
    for (int i = 1; i < n; i++)
        ans1 = min(ans1, f1[i][i + n - 1]), ans2 = max(ans2, f2[i][i + n - 1]);
    cout << ans1 << '\n'
         << ans2;
    return 0;
}

HDU Dire Wolf

原题链接

Problem - 5115 (hdu.edu.cn)

同样是板子题，我们思考发现每次杀一匹狼，最后一次的情形一定是杀最后一匹狼，也就是说这匹狼左边的狼和右边的狼都寄了，所以我们就可以抽象为区间dp问题了

我们定义状态f[l][r]为杀死第l匹到第r匹狼的最小伤害，那么对于每访问过的状态如何转移呢？

考虑最后一次一定是杀一匹狼i，那么我们枚举i，问题就转化为了杀死i在区间[l , r]内左边和右边狼的最小伤害加上狼i的伤害（注意这个狼i可以被区间[l,r]外相邻的狼加buff）

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define int long long
#define N 210
int f[N][N], t, n；
int a[N], b[N];
const int inf = 0x3f3f3f3f3f3f3f3f;
int dfs(int l, int r)
{
    if (l > r)
        return 0;
    if (f[l][r] != inf)
        return f[l][r];
    int &res = f[l][r];
    for (int i = l; i <= r; i++)
        res = min(res, dfs(l, i - 1) + dfs(i + 1, r) + a[i] + b[l - 1] + b[r + 1]);

    return res;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    cin >> t;
    while (t--)
    {
        memset(f, 0x3f, sizeof(f));
        memset(a, 0, sizeof(a));
        memset(b, 0, sizeof(b));

        cin >> n;
        for (int i = 1; i <= n; i++)
            cin >> a[i];
        for (int i = 1; i <= n; i++)
            cin >> b[i];
        cout << "Case #" << idx++ << ": " << dfs(1, n) << '\n';
    }

    return 0;
}

Multiplication Puzzle

原题链接

1651 – Multiplication Puzzle (poj.org)

区间DP板子题，我们采用记忆化搜索来计算状态，即dfs(l,r)为抽走第l张到第r张卡牌获取的最小总点数，用二维数组f[l][r]来剪枝保存

数组a[]来保存每张牌的点数，初始化为-1

如果l > r，那么返回0

如果f[l][r]已经访问，那么直接返回

如果未访问，那么有f[l][r] = min(f[l][r] , dfs(l, i - 1) + dfs(i + 1, r) + abs(a[i] * a[l - 1] * a[r + 1]))

代码甚至没怎么变

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 210
int f[N][N], t, n;
int a[N];
const int inf = 0x3f3f3f3f3f3f3f3f;
int dfs(int l, int r)
{
    if (l > r)
        return 0;
    if (f[l][r] != inf)
        return f[l][r];

    int &res = f[l][r];
    for (int i = l; i <= r; i++)
        res = min(res, dfs(l, i - 1) + dfs(i + 1, r) + abs(a[i] * a[l - 1] * a[r + 1]));
    return res;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    // freopen("in.txt", "r", stdin);
    // freopen("out.txt", "w", stdout);
    memset(f, 0x3f, sizeof(f));
    memset(a, -1, sizeof(a));

    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    cout << dfs(2, n - 1);
    return 0;
}

Polygon

原题链接

1179 – Polygon (poj.org)

这个题就涉及到我们前面区间DP分析中说的，二维状态已经不满足需求，需要增加辅助维度

这道题之所以需要加辅助维度，其实看完题就能明白，这种经典最大值可能是两个负数相乘

所以我们直接跑板子得到的不一定是最大值

我们还是自下而上的分析，最后一步自然是合并两个点为一个点，然后游戏结束了，那么问题转化为左区间合并最值和右区间合并最值

我们开两个二维数组（也可以开成第三个维度长度为2的三维数组），f存最大值，g存最小值，f[l][r]就是删除编号l到r的点的最大得分

读数据同样倍增一倍，破环为链，然后跑递推（记忆化搜索也行，主函数一层循环记忆化搜索）

枚举长度，对于长度为1的，即一个点，那么最大值最小值就是这个点的值

否则，我们枚举左子区间的右边界，区间最大值最小值由两个子区间最大值最小值共同转移

代码相比前面长了一点，但其实还是一个板子，没什么复杂的。

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 110, INF = 1 << 15;
int w[N], f[N][N], g[N][N] , n;
char op[N];

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);//poj没nullptr
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> op[i] >> w[i];
        op[i + n] = op[i], w[i + n] = w[i];
    }
    for (int len = 1; len <= n; len++)
    {
        for (int l = 1; l <= n * 2 - len + 1; l++)
        {
            int r = l + len - 1;

            if (len > 1)//分支预测常数优化
            {
                f[l][r] = -INF, g[l][r] = INF;
                for (int k = l; k < r; k++)
                {
                    char c = op[k + 1];
                    int minl = g[l][k], minr = g[k + 1][r];
                    int maxl = f[l][k], maxr = f[k + 1][r];
                    if (c == 't')
                    {
                        f[l][r] = max(f[l][r], maxl + maxr);
                        g[l][r] = min(g[l][r], minl + minr);
                    }
                    else
                    {
                        int x1 = maxl * maxr, x2 = maxl * minr, x3 = minl * maxr, x4 = minl * minr;
                        f[l][r] = max(f[l][r], max(max(x1, x2), max(x3, x4)));
                        g[l][r] = min(g[l][r], min(min(x1, x2), min(x3, x4)));
                    }
                }
            }
            else
                f[l][r] = g[l][r] = w[l];
        }
    }
    int res = -INF;
    for (int i = 1; i <= n; i++)
        res = max(res, f[i][i + n - 1]);
    cout << res << endl;

    for (int i = 1; i <= n; i++)
        if (res == f[i][i + n - 1])
            cout << i << " ";
    return 0;
}