百万数据集测试赛题秒级查询的MySQL方案

比赛题目

最佳解法

solution_row

prime_encoded

比赛题目

有一张表 cards，id 是自增字段的数字主键，另外有4个字段 c1,c2,c3,c4 ，每个字段随机从 1~10 之间选择一个整数，要求选手使用一条 SQL 给出 24 点的计算公式，返回的内容示例如下图：

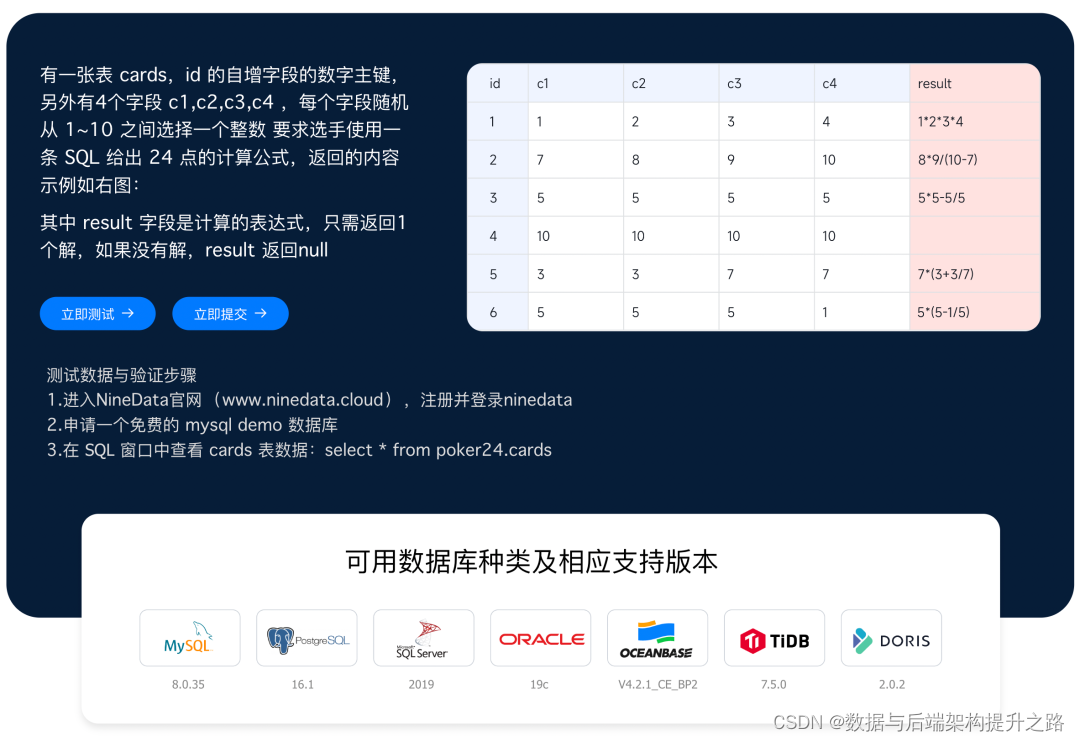
最佳解法

参赛数据库：MySQL

性能评测：百万级数据代码性能评测 0.67秒

综合得分：95

以下是代码说明思路简介：

0、核心：因为4张牌计算24点时的顺序可任意互换，所以不同排列的4张牌可视为同一组合。采用质数编码，把1到10映射成2到29内的质数，4张牌的积可作为该组合的唯一编码

1、本地写代码，通过简单的回溯算法，生成24点游戏的所有解，按照152,((1+1)+1)*8,156,(6*2)*(1+1),...即"质数乘积:解决方案表达式" 的格式输出(质数表达式对应的质数在这步算好，而不放如mysql可以提高计算速度)

生成4个1-10可重复的所有组合
通过回溯减枝给定的4个数判断是否符合24点，核心思路可以参考力扣的679. 24 点游戏
按照"质数乘积:解决方案表达式" 的格式整理输出

import itertools

TARGET = 24
EPSILON = 1e-6
ADD, MULTIPLY, SUBTRACT, DIVIDE = 0, 1, 2, 3


def generate_expr(nums, current_exprs=None):
    if current_exprs is None:
        current_exprs = [(str(num), num) for num in nums]

    if len(current_exprs) == 1:
        _, value = current_exprs[0]
        if abs(value - TARGET) < EPSILON:
            return [current_exprs[0][0]]
        return []

    results = []
    size = len(current_exprs)
    for i in range(size):
        for j in range(size):
            if i != j:
                next_exprs = [current_exprs[k] for k in range(size) if k != i and k != j]
                for op in range(4):
                    if op < 2 and i > j:
                        continue

                    expr1, val1 = current_exprs[i]
                    expr2, val2 = current_exprs[j]
                    new_expr = ""

                    if op == ADD:
                        new_expr = f"({expr1}+{expr2})"
                        next_exprs.append((new_expr, val1 + val2))
                    elif op == MULTIPLY:
                        new_expr = f"({expr1}*{expr2})"
                        next_exprs.append((new_expr, val1 * val2))
                    elif op == SUBTRACT:
                        new_expr = f"({expr1}-{expr2})"
                        next_exprs.append((new_expr, val1 - val2))
                    elif op == DIVIDE:
                        if abs(val2) < EPSILON:
                            continue
                        new_expr = f"({expr1}/{expr2})"
                        next_exprs.append((new_expr, val1 / val2))

                    sub_results = generate_expr([], next_exprs)
                    for result in sub_results:
                        results.append(result)
                    next_exprs.pop()

    return results

def find_prime_factor_product(nums):

    #1-10分别映射如下字段
    prime_map = {index+1: prime for index, prime in enumerate([2, 3, 5, 7, 9, 11, 13, 17, 19, 23])}
    result = 1

    for num in nums:
          result = result * prime_map[num]

    return result
def eval_expr(expr):
    try:
        return abs(eval(expr) - 24) < 1e-6
    except ZeroDivisionError:
        return False


def find_expressions_for_24(nums):
    results = set()

    for p_nums in set(itertools.permutations(nums)):
        for expr in generate_expr(list(p_nums)):
            # 符合24点
            if eval_expr(expr):
                results.add(expr)
    return results


# Generate all combinations of 4 numbers from 1 to 10, without considering permutations
all_combinations = set(itertools.combinations_with_replacement(range(1, 11), 4))

# Find all expressions that result in 24 for each combination
expressions_resulting_in_24 = {}
for combo in all_combinations:
    prime_factors_product = find_prime_factor_product(combo)
    expressions = find_expressions_for_24(combo)
    if expressions:
        expressions_resulting_in_24[prime_factors_product] = expressions

# Display the results
for combo, exprs in list(expressions_resulting_in_24.items()):
    print(f"Combination {combo}:")
    for expr in exprs:
        print(f"  {expr}")
    print()

打印结果如下：

Combination 486:
(1-(2-(5*5)))
((1+(5*5))-2)
(1+((5*5)-2))
((5*5)-(2-1))
((1-2)+(5*5))
((5*5)+(1-2))

Combination 5049:
(8*(2+(6-5)))
((2-8)+(6*5))

.........

2、受限于代码大小10k限制，通过把上一步生成的数据进行压缩：SELECT REPLACE(TO_BASE64(COMPRESS('(4/1)*(3*2),2/(1/(4*3)),((3*4)*2)/1,...'))...')), '\n', '')

SELECT REPLACE(TO_BASE64(COMPRESS('(4/1)*(3*2),2/(1/(4*3)),((3*4)*2)/1,...')), '\n', '') AS compressed_base64;

3、提交的代码中，先对上一步生成的数据解压缩：UNCOMPRESS(FROM_BASE64('XXXX'))，并通过递归CTE生成查询表：(4/1)*(3*2);2/(1/(4*3));((3*4)*2)/1,...'));...

SELECT UNCOMPRESS(FROM_BASE64('XXXX')) AS decompressed_data;

4、对输入表LEFT JOIN上一步生成的查询表，关联的键值是对c1，c2，c3，c4做质数编码后的积。

以下是如何在MySQL中使用CTE来分割由分号分隔的字符串的完整示例。假设solution_str是一个由分号分隔的24点游戏解的长字符串，每个解之间用分号分隔。

-- 生成1到10的数字
WITH RECURSIVE number_list AS (
  SELECT 1 AS n
  UNION ALL
  SELECT n + 1 FROM number_list WHERE n < 10 
),
--prime_numbers 表包含一个映射，它将数字1到10映射到它们对应的质数
prime_numbers AS (
  SELECT n, ELT(n, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29) AS prime FROM number_list -- 映射1-10到质数
),
solution_set AS (
  SELECT CAST(UNCOMPRESS(FROM_BASE64('XXXX')) AS CHAR) AS solution_str -- 假设XXXX是压缩且编码后的字符串
),

--将24点计算表达式解决方案的长字符串分解为单独的行，每行一个解决方案，同时记录编号
solution_rows AS (
  SELECT 
    SUBSTRING_INDEX(SUBSTRING_INDEX(sub_solution.solution, ';', numbers.n), ';', -1) AS solution_pair,
    numbers.n + 1 AS next_n
  FROM solution_set
  JOIN (
    SELECT n FROM number_list
  ) AS numbers ON CHAR_LENGTH(solution_str) 
  - CHAR_LENGTH(REPLACE(solution_str, ';', '')) >= numbers.n - 1
),
split_solutions AS (
  SELECT 
    SUBSTRING_INDEX(solution_pair, ':', 1) AS prime_product,
    SUBSTRING_INDEX(solution_pair, ':', -1) AS solution_expression
  FROM solution_rows
),
prime_encoded AS (
  SELECT id, 
    (SELECT prime FROM prime_numbers WHERE n = c1) *
    (SELECT prime FROM prime_numbers WHERE n = c2) *
    (SELECT prime FROM prime_numbers WHERE n = c3) *
    (SELECT prime FROM prime_numbers WHERE n = c4) AS prime_product 
    --cards 表有多列，其中每列（c1, c2, c3, c4）都包含1到10之间的数字 
 FROM cards
)
SELECT c.*, s.solution
FROM prime_encoded AS c
LEFT JOIN solution_rows AS s ON c.prime_product = s.prime_product;

solution_row

可以理解为决方案的长字符串和num_list中不超过N+1的数字逐个关联

solution_str 是一个包含多个解决方案的长字符串，其中每个解决方案由分号分隔。
CHAR_LENGTH(solution_str) 计算solution_str的总字符数。
REPLACE(solution_str, ';', '') 将solution_str中的所有分号替换为空字符，从而移除所有分号。
CHAR_LENGTH(REPLACE(solution_str, ';', '')) 计算移除分号后的字符串长度。
CHAR_LENGTH(solution_str) - CHAR_LENGTH(REPLACE(solution_str, ';', '')) 这个表达式计算原始字符串和移除分号后字符串长度的差值。这个差值实际上就是原始字符串中分号的数量。因为每个分号被替换为一个空字符，每替换一个分号，长度就减少一个字符。
>= numbers.n - 1 这部分是用来确保当前数字（来自numbers CTE）不超过分号的数量加1。因为如果有N个分号，那么就有N+1个解决方案。

prime_encoded

card表的每个字段添加对应的质数字段

每次SELECT prime FROM prime_numbers WHERE n = c1（以及对于c2, c3, c4）的子查询都会返回c1（以及c2, c3, c4）对应的质数。然后将这些质数相乘，生成一个唯一的prime_product，它代表了该行的四个数字的一个唯一编码。
最终，prime_encoded CTE返回两列：原始表cards的id和计算出的prime_product。