多平面包络的圆柱体参数估计

场景

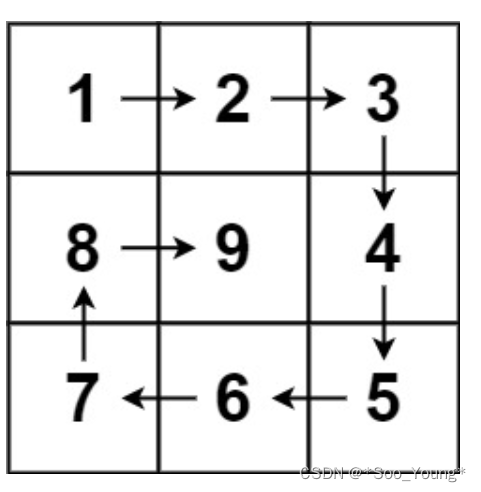
现有多个空间平面包络一个柱体，从圆柱顶端俯视如图所示：

中心位置为圆柱实际所在位置。现在已知这些平面的参数（每个平面的方程均为ax+by+cz+d=0形式, 参数为a,b,c,d），希望求解它们包络的这个圆柱的几何信息。

分析

三维空间中，圆柱的几何信息有两类表达方式：

1. 圆柱中轴的方向向量$(u,v,1)$和中轴上一点坐标$(x,y,z)$，以及半径r。
2. 圆柱顶面中心点坐标$(x_1,y_1,z_1)$，底面中心点坐标$(x_2,y_2,z_2)$，以及半径r。
   前一种表达方式具有最少的参数量，描述了一个无限高度的空间圆柱体；后一种表达方式多了一个参数，本质上限定了圆柱顶面和底面的位置。

已知的几何约束包括：

1. 中轴垂直于所有平面的法向量。
2. 中轴必定被所有平面包围在内部。
3. 中轴上任意一点到各平面的距离相等且非0，这个距离就是半径r。

求解方案

多平面包络圆柱体只能是在局部范围内包络。受计算机数值精度影响，很难使所有平面完美相切同一圆柱体，因而很可能出现在不同的Z坐标处所包络的圆柱体半径不同的情况。此外，如果没有Z坐标，我们只能得到空间直线的方程，实际上没有太大用处，不易基于它来求半径。因此一个关键要素就是：先验的Z值。

根据应用场景，我们假定有先验估算的z坐标最小值和最大值。
由于没有任何一个平面过中轴，而是仅仅与圆柱体表面相切，中轴上点的位置无法直接求解。可以考虑先求解中轴的方向，再求中轴上一点的坐标和半径。

求解方法一：

1. 由于已知所有平面的参数a、b、c、d，可以直接求出中轴方向：当仅有两个不相交平面时，即可用它们法向量的叉积直接得到中轴方向；平面数量更多时，需要使用最小二乘法求解最佳的中轴方向。
2. 先取出圆柱体中轴上一点的z坐标近似值$z_0$。
3. 将该$z_0$代入所有平面方程，求解中轴上z坐标为$z_0$的一点的x,y坐标近似值。由于中轴在多平面包络的内部，因此只需将平面两两相交的交点重心作为x,y坐标近似值$(x^{\prime },y^{\prime })$。
4. x,y坐标精化和半径r求解。这一步利用约束3，列出约束条件方程：
   $$|\frac{|a{x}_0+b{y}_0+c{z}_0+d|}{\sqrt{a^2+b^2+c^2}}-r|=0$$
   其中$(x_0,y_0,z_0)$是待求的中轴点坐标（$z_0$已知）。由于带有绝对值符号，求解存在一定困难，可以考虑使用下面的形式：
   $$\frac{(a{x}_0+b{y}_0+c{z}_0+d{)}^2}{a^2+b^2+c^2}-r^2=0$$
   求解的初始值使用近似值$(x^{\prime },y^{\prime })$，半径取正实数即可。
5. 当近似值$(x^{\prime },y^{\prime })$偏差不太大时，即可得到较好的解：中轴上一点$(x_0,y_0,z_0)$，中轴方向和半径$r$。

注意到，中轴方向的求解和半径、中轴点求解是分离的。由此产生解法二：

1. 取到圆柱体的z坐标范围$z_{min},z_{max}$。
2. 将$z_{min}$代入所有平面方程，求解中轴上z坐标为$z_{min}$的一点的x,y坐标近似值。
3. 将$z_{max}$代入所有平面方程，求解中轴上z坐标为$z_{max}$的一点的x,y坐标近似值。
4. $z_{min},z_{max}$对应的x,y坐标精化和半径r求解。求解的初始值使用上一步得到的近似值，半径取正实数即可。为使求解更严谨，可以将两组方程列在一起求解唯一的r。
5. 当近似值与真实值偏差不太大时，可得到较好的解：中轴两点$(x_{min},y_{min},z_{min})$、$(x_{max},y_{max},z_{max})$和半径$r$。

求解效果

初始中轴点求解效果：

可见，初始点位在平面包络的内部空间，可以进行下一步精化、半径求解。

最终的可视化结果如图：