目录
- 引言
- 一、并查集概念
- 二、并查集模板
- 三、例题
- 1.合并集合
- 2.连通块中点的数量
引言
这个并查集以代码短小并且精悍的特点,在算法竞赛和面试中特别容易出,对于面试而言,肯定不会让你去写一两百行的代码,一般出的都是那种比较短的,而且还不好想考验思维的那种题,那并查集就将这两点全占了,所以重要性很大,而且竞赛的话也就是将多个知识点合并起来考察,这个也很可能成为一个点,所以话不多说就开始吧。
一、并查集概念
-
并查集主要有两个作用:
1.查询两个元素是否在同一集合中,时间复杂度近乎O(1)
2.将两个集合合并 -
初始化思路:首先有多个元素,它们最初每个集合只有它们自己,有个p[N]数组,p[i]代表 i 号结点的父结点的下标,p [i] = i
-
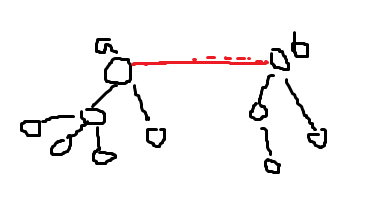
合并思路:先查询它们各自的父结点a,b,然后让p [a] = b 意为a的父亲为b这样a所在的集合就与b所在的集合合并了,如下图所示
-
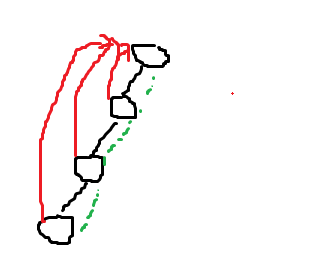
查询思路:查询自己的父结点是不是根结点,如果是返回,不是则继续递归再次查找父结点的父结点,最后返回根结点,这个是通过递归实现的,这里有个路径压缩的过程,就是最后一个是根结点就会返回,那么就把根结点赋给倒数第三层、第四层…,也就是让每一个结点都指向根结点,类似就是下图所示
二、并查集模板
void init()
{
for(int i = 1; i <= n; ++i) p[i] = i;
}
int find(int x) //查询编号为x的父结点
{
if(p[x] != x) p[x] = find(p[x]); //说明不是父结点,让当前结点指向父结点的父结点,也就是最终的根结点
return p[x]; //返回父结点
}
三、例题
1.合并集合
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤105
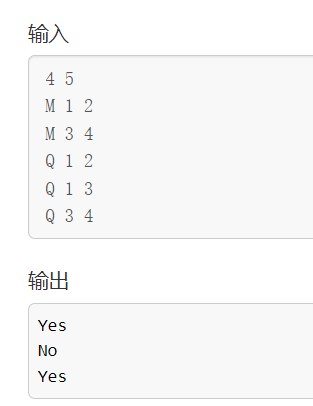
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e5+10;
int p[N]; //p[i]代表i的父节点的编号
int n, m; //n个结点,m次询问
void init()
{
for(int i = 1; i <= n; ++i) p[i] = i;
}
int find(int x) //查询编号为x的父结点
{
if(p[x] != x) p[x] = find(p[x]); //说明不是父结点,让当前结点指向父结点的父结点,也就是最终的根结点 ,注意这里不能写成find(p[x])不然条件就一直没有变化
return p[x]; //返回父结点
}
int main()
{
scanf("%d%d", &n, &m);
init();
while(m--)
{
char op[2];
int a, b;
scanf("%s%d%d", op, &a, &b);
if(!strcmp(op, "M"))
{
a = find(a), b = find(b); //找到a和b的根结点
p[a] = b; //让a指向b,意为a的父亲为b,那么a下的所有结点的父亲都是b
}
else
{
if(find(a) == find(b)) printf("Yes\n"); //如果两个结点的根结点相同,则在同一个集合
else printf("No\n");
}
}
return 0;
}
所有的用例都通过了

2.连通块中点的数量
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;
Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;
Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
const int N = 1e5+10;
int p[N], cnt[N]; //来判断根结点所对应的集合的数量,只有根结点有意义
int n, m;
int find(int x)
{
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main()
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i) p[i] = i;
for(int i = 1; i <= n; ++i) cnt[i] = 1;
while(m--)
{
char op[5];
int a, b;
scanf("%s", op);
if(!strcmp(op,"C"))
{
scanf("%d%d", &a, &b);
a = find(a), b = find(b);
if(a == b) continue;
p[a] = b;
cnt[b] += cnt[a];
}
else if(!strcmp(op,"Q1"))
{
scanf("%d%d", &a, &b);
if(find(a) == find(b)) printf("Yes\n");
else printf("No\n");
}
else
{
scanf("%d", &a);
printf("%d\n", cnt[find(a)]);
}
}
return 0;
}