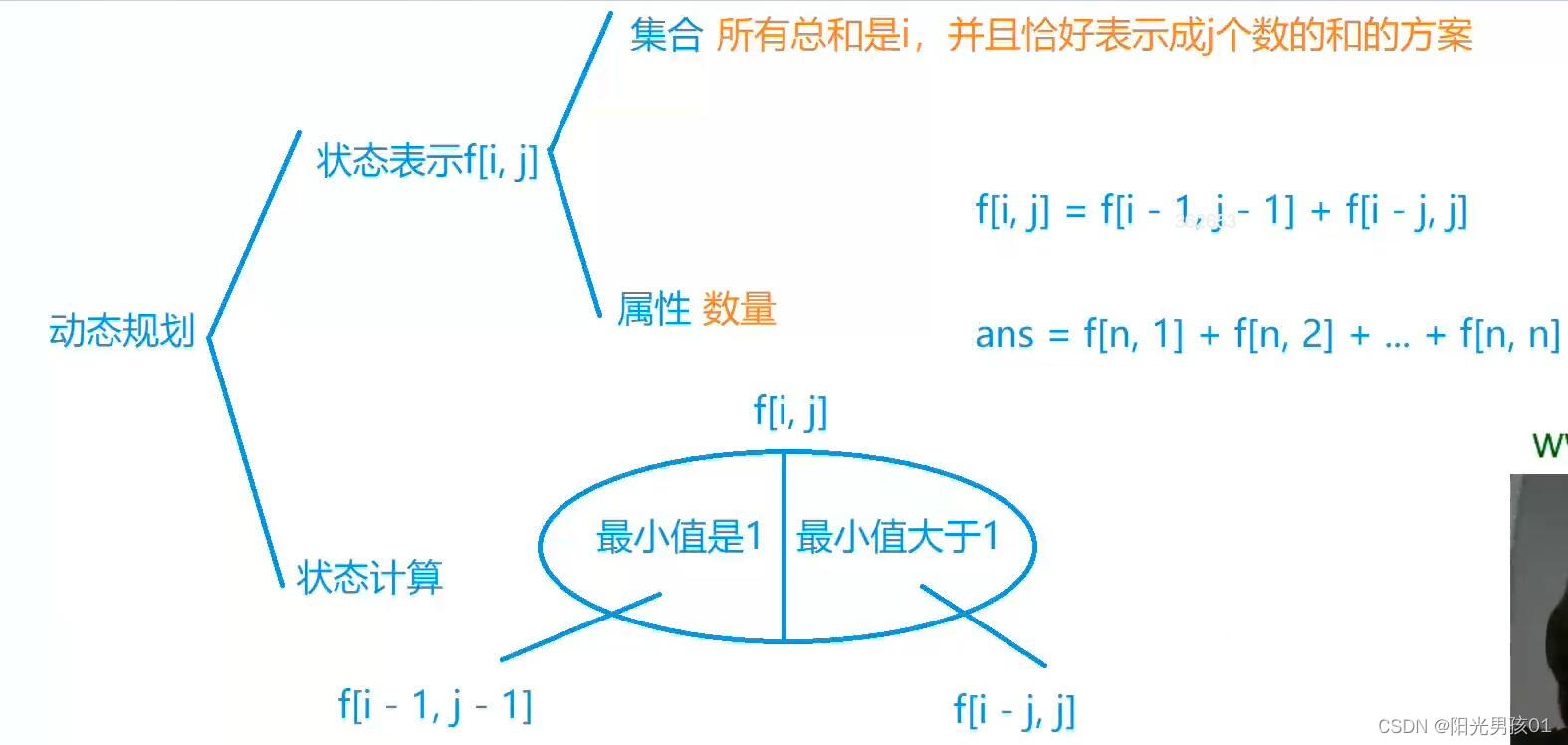
动态规划
动态规划就像是解决问题的一种策略,它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题,并将每个小问题的解保存起来。这样,当我们需要解决原始问题的时候,我们就可以直接利用已经计算好的小问题的解,而不需要重复计算。
动态规划与数学归纳法思想上十分相似。
数学归纳法:
-
基础步骤(base case):首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况,可以直接验证命题是否成立。
-
归纳步骤(inductive step):假设命题在某个情况下成立,然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。
通过反复迭代归纳步骤,我们可以推导出命题在所有情况下成立的结论。
动态规划:
-
状态表示:
-
状态转移方程:
-
初始化:
-
填表顺序:
-
返回值:
数学归纳法的基础步骤相当于动态规划中初始化步骤。
数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。
动态规划的思想和数学归纳法思想类似。
在动态规划中,首先得到状态在最小的基础情况下的值,然后通过状态转移方程,得到下一个状态的值,反复迭代,最终得到我们期望的状态下的值。
接下来我们通过三道例题,深入理解动态规划思想,以及实现动态规划的具体步骤。、
740. 删除并获得点数
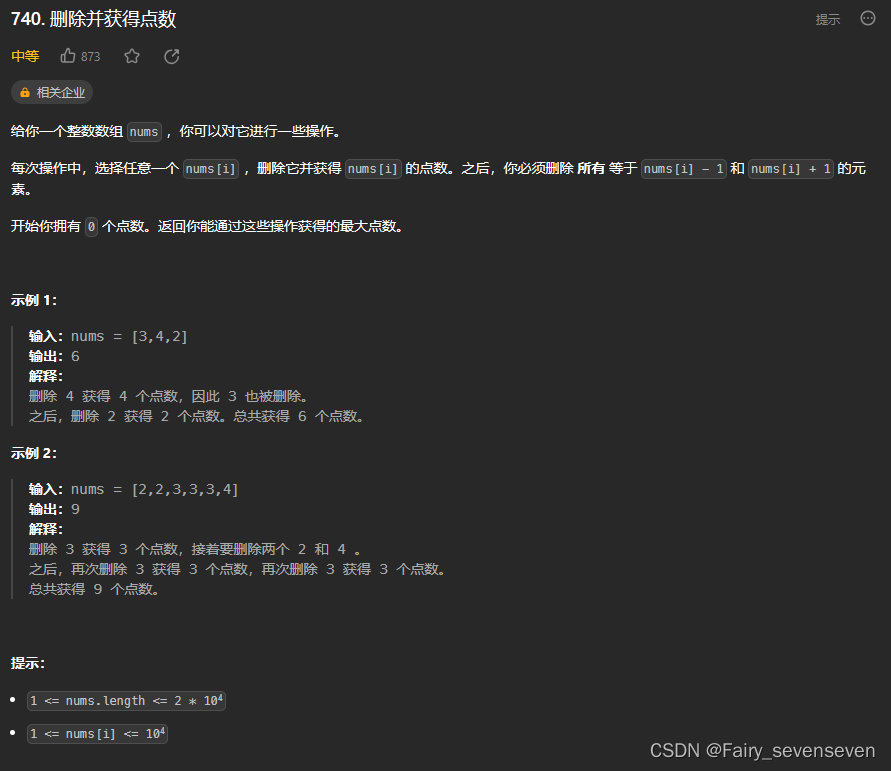
题目解析

我们发现选择了一个数字,假设是x,那么x+1和x-1我们都不能再选择,这种模式非常像打家劫舍题目的模式。由此我们可以把此问题转化为打家劫舍问题。

由于1<=nums[i]<=1e4,所以我们可以创建一个1e4+1大小的数组count,count[i]表示i数字拥有的点数,也就是i*(i出现的次数),这样我们就可以把原问题转化为打家劫舍问题。
状态表示
我们将nums数组转化为count数组,接着对count数组分析即可。
我们可以定义dp[i]表示,1到i 这些数中,我们选择其中不相邻的部分项,所能得到的最大点数。
状态转移方程
我们想一想dp[i]怎么由其他的状态推导出来。
dp[i]表示,1到i 这些数中,我们选择其中不相邻的部分项,所能得到的最大点数。
dp[i-1]表示,1到i-1 这些数中,我们选择其中不相邻的部分项,所能得到的最大点数。
dp[i-2]表示,1到i-2 这些数中,我们选择其中不相邻的部分项,所能得到的最大点数。
我们对i的状态进行研究,一共可以分为两种情况,要么1-i这些数中,我们选择其中不相邻的部分项,其中选择了i,要么我们不选择i。
当我们选择i,那我们就不可能选择i-1,所以此时最大的点数应该是dp[i-2]+count[i]
如果我们不选择i,那我们就可以选择i-1,此时最大的点数应该是dp[i-1],也就是从1到i-1这些数选择不相邻的部分项所能获得的最大点数。
故状态转移方程为,dp[i]=max(dp[i-2]+count[i],dp[i-1])
初始化
由状态转移方程我们知道,想要推导出i位置的状态,需要用到i-1和i-2位置的状态,所以我们需要初始化前两个位置的状态,也就是下标1和2。因为count[0]是不考虑的,nums>=1。
很容易可以得出。
dp[0]=count[0]
dp[1]=max(count[0],count[1])
填表顺序
从左到右
返回值
返回最后一个元素即dp[1e4]
代码实现
int deleteAndEarn(int* nums, int numsSize) {
int n=numsSize;
const int m=1e4+1;
int count[m];
memset(count,0,sizeof(count));
for(int i=0;i<n;i++){
count[nums[i]]+=nums[i];
}
int dp[m];
dp[1]=count[1];
dp[2]=fmax(count[1],count[2]);
for(int i=3;i<=1e4;i++){
dp[i]=fmax(dp[i-2]+count[i],dp[i-1]);
}
return dp[m-1];
}我们知道nums中存储的数字的范围是1到1e4,所以我们可以利用count数组, 定义count[i]表示i数字拥有的点数,我们只需要对count数组做一次打家劫舍就可以了。
LCR 091. 粉刷房子

题目解析

状态表示
如果我们定义dp[i]表示从0号房子到i号房子,我们选择不同的粉刷方案,所花费的最小金额数,我们想一想此状态表示的状态转移方程怎么推导?我们具体分析i号房子的状态,一共有三种情况,要么i号房子粉刷成红色,要么i号房子粉刷成绿色,要么i号房子粉刷成蓝色。对于这三中国情况,我们没办法只通过前面几个房子的最小花费数而得到i号房子的最小花费数,因为当我确定i号房子的粉刷颜色,前面的房子的粉刷颜色我没办法确定。所以我们的状态表示应该还需要包括粉刷的颜色。
我可以对其改进,定义dp[i][j]表示从0号房子开始到i号房子,选择不同的粉刷方案,且i号房子粉刷j颜色时的最小花费。其中j的取值是0、1或者2,分别表示红色绿色蓝色。
这样我们就是推导出状态转移方程,一步一步推导状态。
状态转移方程
我们想一想dp[i][j]的状态值如何通过其他的状态推导出来。
dp[i][j]表示从0号房子开始到i号房子,选择不同的粉刷方案,且i号房子粉刷j颜色时的最小花费。
dp[i-1][j]表示从0号房子开始到i-1号房子,选择不同的粉刷方案,且i号房子粉刷j颜色时的最小花费。
对于i号房子,我们依旧分为三种情况,要么粉刷红色要么粉刷绿色要么粉刷蓝色。
当我们对i号房子粉刷红色时,很明显,dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i][0]
i-1号房子粉刷的颜色不能是红色,要么是绿色要么是蓝色,从0号房子到i-1号房子,且i-1号房子粉刷成绿色蓝色时最小的花费分别是dp[i-1][1],dp[i-1][2]
选择较小的一个然后加上i号房子粉刷红色的花费就是dp[i][0]
同理dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i][1]
dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i][2]
故,状态转移方程为
dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i][0]
dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i][1]
dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i][2]
初始化
根据状态转移方程,我们知道推导出i房子粉刷红绿蓝三个状态需要i-1号房子的三个状态,所以我们需要初始化第一个房子的三个状态值。
即,
dp[0][0]=costs[0][0]; dp[0][1]=costs[0][1]; dp[0][2]=costs[0][2];
填表顺序
从左往右填写,一次填写三个状态
返回值
返回最后一个房子三个状态中最小的那个花费。
即,return fmin(dp[n-1][0],fmin(dp[n-1][1],dp[n-1][2]));
代码实现
int minCost(int** costs, int costsSize, int* costsColSize){
int n=costsSize;
int dp[n][3];
dp[0][0]=costs[0][0];
dp[0][1]=costs[0][1];
dp[0][2]=costs[0][2];
for(int i=1;i<n;i++){
dp[i][0]=fmin(dp[i-1][1],dp[i-1][2])+costs[i][0];
dp[i][1]=fmin(dp[i-1][0],dp[i-1][2])+costs[i][1];
dp[i][2]=fmin(dp[i-1][0],dp[i-1][1])+costs[i][2];
}
return fmin(dp[n-1][0],fmin(dp[n-1][1],dp[n-1][2]));
}309. 买卖股票的最佳时机含冷冻期
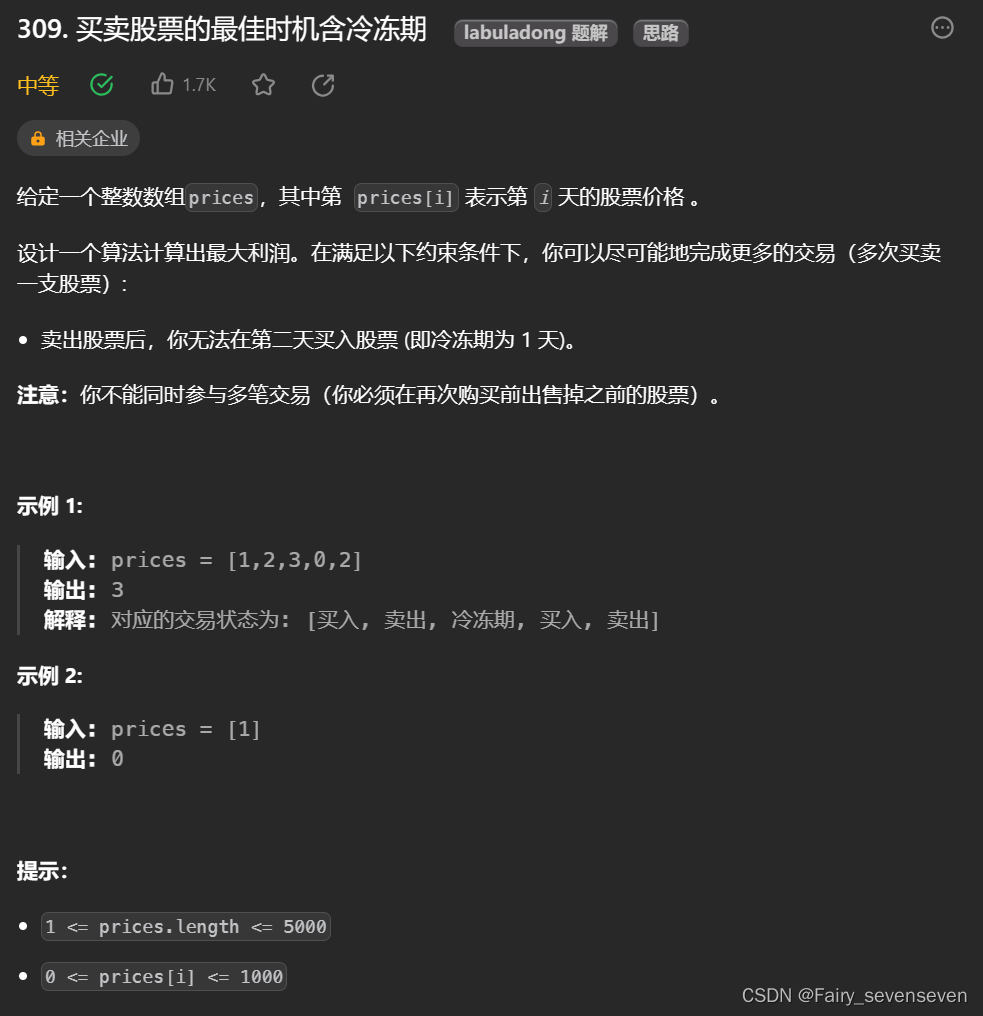
题目解析

状态表示
如果我们定义dp[i]表示从第0天开始到第i天,我们所得到利润的最大值,我们没办法通过其他的状态值推导出i位置的状态值。仔细想想,其实第i天的状态还可以细分。
可以分为第i天结束时,手上有股票,或者手上没股票且在冷冻期,或者手上没股票且不在冷冻期。
所以我们可以定义 dp[i][j]表示从第0天到第i天,所获得的最大利润值,且第i天结束时拥有状态j(j=0表示手上有股票,j=1表示手上没股票,且在冷冻期,j=2表示手上没股票,且不在冷冻期)。
状态转移方程
我们想一想第i天的三个状态能不能由其他的状态推导得出。
dp[i][j]表示从第0天到第i天,所获得的最大利润值,且第i天结束时拥有状态j
dp[i-1][j]表示从第0天到第i-1天,所获得的最大利润值,且第i天结束时拥有状态j
(j=0表示手上有股票,j=1表示手上没股票,且在冷冻期,j=2表示手上没股票,且不在冷冻期)。
当第i天结束的时候,我们手上有股票,对应dp[i][0],说明第i天白天我们买了股票,或者第i-1天我们手上有股票,且第i天白天我们没有卖掉。
也就是第i-1天结束时,要么是手上有股票,要么是手上没股票且不在冷冻期。
所以dp[i][0]=max(dp[i-1][0],dp[i-1][2]-prices[i])
第i天买了股票,所以利润需要减去股票价值。
当第i天结束的时候,我们手上没有股票,且在冷冻期,对应dp[i][1],说明第i天白天我们卖了股票,所以在第i天结束的时候处于冷冻期。所以要么第i-1天手上有股票,然后第i天白天我们卖掉了,要么第i-1天我们手上没有股票且不在冷冻期,第i天白天我们买了股票又卖了股票。
所以dp[i][1]=max(dp[i-1][0]-prices[i],dp[i-1][2])
当第i天结束的时候,我们手上没有股票,且不在冷冻期,对应 dp[i][2],说明第i天白天我们没有卖股票,要么i-1天白天我们卖了股票,要么i-1天白天也没卖股票,然后第i天白天什么都没做。也就是i-1天结束时的状态要么是手上没股票,且在冷冻期,要么是手上没股票,且不在冷冻期。(i-1天结束时的状态要么是手上没股票,且在冷冻期,然后冷冻期一直持续到第i天结束前,结束时冷冻期结束。)
所以dp[i][2]=max(dp[i-1][1],dp[i-1][2])
故状态转移方程为,
dp[i][0]=fmax(dp[i-1][0],dp[i-1][2]-prices[i]); dp[i][1]=fmax(dp[i-1][0]+prices[i],dp[i-1][2]); dp[i][2]=fmax(dp[i-1][1],dp[i-1][2]);
初始化
通过状态转移方程,我们知道推导出i天的状态需要i-1天的状态,所以我们需要初始化第0天的三个状态。
dp[0][0]表示第0天结束时手上有股票,说明白天买了股票,利润为负的prices[0]。
dp[0][1]表示第0天结束时手上没有股票,且在冷冻期,不可能存在的状态,所以该状态的值不能影响后面的状态,利润置0就可以了。因为会取到这个值的状态转移方程是dp[i][2]=fmax(dp[i-1][1],dp[i-1][2]);利润置0,dp[i-1][2]不为零,就不会取到dp[i-1][1],dp[i-1][2]为零,dp[i-1][1]也不会影响dp[i]的推导。
dp[0][2] 表示第0天结束时手上没有股票,且不在冷冻期,说明白天没有卖股票,dp[0][2]=0;
所以初始化为,
dp[0][0]=-prices[0]; dp[0][1]=0; dp[0][2]=0;
填表顺序
从左往右填写,一次性填写三个状态
返回值
返回最后一天中,三个状态的最大值,即
return fmax(dp[n-1][0],fmax(dp[n-1][1],dp[n-1][2]));
代码实现
int maxProfit(int* prices, int pricesSize) {
int n=pricesSize;
int dp[n][3];//0:有票 1:无票且在冷冻期 2:无票且不在冷冻期
dp[0][0]=-prices[0];
dp[0][1]=0;
dp[0][2]=0;
for(int i=1;i<n;i++){
dp[i][0]=fmax(dp[i-1][0],dp[i-1][2]-prices[i]);
dp[i][1]=fmax(dp[i-1][0]+prices[i],dp[i-1][2]);
dp[i][2]=fmax(dp[i-1][1],dp[i-1][2]);
}
return fmax(dp[n-1][0],fmax(dp[n-1][1],dp[n-1][2]));
}结尾
今天我们学习了动态规划的思想,动态规划思想和数学归纳法思想有一些类似,动态规划在模拟数学归纳法的过程,已知一个最简单的基础解,通过得到前项与后项的推导关系,由这个最简单的基础解,我们可以一步一步推导出我们希望得到的那个解,把我们得到的解依次存放在dp数组中,dp数组中对应的状态,就像是数列里面的每一项。最后感谢您阅读我的文章,对于动态规划系列,我会一直更新,如果您觉得内容有帮助,可以点赞加关注,以快速阅读最新文章。
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!