坚持看完,结尾有思维导图总结
这里写目录标题
- 什么是二叉树?
- 二叉树的定义
- 二叉树的性质
- 二叉树的基石在哪里?
- 总结
什么是二叉树?
二叉树的定义
二叉树,就是从一个根开始,按照两边分支的方式向下生长的树,就能看成二叉树
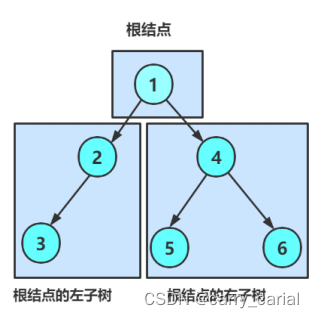
二叉树有这些特性
- 可以区分成根节点,左子树和右子树,有序
- 不存在度大于2的节点
并且要区分一下几种情况
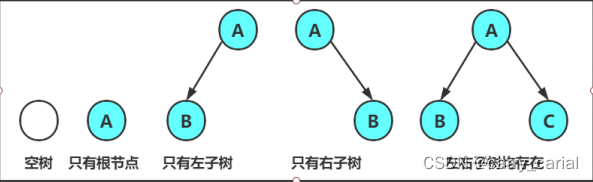
二叉树的性质
常用的有以下性质:
- 如果首个根节点的层数是 1 ,那么深度为 h 的二叉树最大节点数是 2^h - 1
- 一个非空二叉树第 i 层上最多有 2^(i - 1) 个结点
- 对于任何一个二叉树,如果一个有度为 0 的叶节点个数为 n0, 度为2的节点个数是 n2 个 ,可以得到 n0 = n2+1
- 如果首节点层数是 1 ,那么拥有 n 个结点的满二叉数的深度 h = log2(n + 1)
二叉树的基石在哪里?
二叉树的基石在遍历,二叉树有四种遍历方式
前序遍历,中序遍历,后序遍历,层序遍历
不是构建二叉树什么的,而是给定一个二叉树的不同方式的访问更加重要
之后会用动图来说明谦前序遍历,中序遍历,后续遍历和层序遍历
然后给出程序实现
首先先定义二叉树的节点,拥有存储数据,左节点和右节点
typedef int TreeDate;
typedef struct TreeNode{
TreeDate val;
struct TreeNode* left;
struct TreeNode* right;
}TreeNode ;
前序遍历
步骤
先访问根节点,
然后访问左子树,
之后再访问右子树

通过分析,访问节点的顺序是
3 8 2 NULL 3 NULL 4 0 NULL NULL 1 NULL NULL
//访问没有返回值,传入根节点
void PreOrder(TreeNode* root)
{
//遇到空节点返回
if(root == NULL)
{
return;
}
//打印根节点
printf("%d",root->TreeDate);
//访问左右子树
PreOrder(root->left);
PreOrder(root->right);
}
程序执行的结果是

中序遍历
按照先左子树,再根节点,再右子树的顺序遍历

//访问没有返回值,传入根节点
void MidOrder(TreeNode* root)
{
//遇到空节点返回
if(root == NULL)
{
return;
}
//访问左子树
MidOrder(root->left);
//打印根节点
printf("%d",root->TreeDate);
//访问右子树
MidOrder(root->right);
}
我们可以发现,和上面的程序除了打印的顺序和递归的顺序不一样,其余的都相同
后序遍历
先访问右子树,再访问左子树,最后访问根节点
void BackOrder(TreeNode* root)
{
//遇到空节点返回
if(root == NULL)
{
return;
}
//访问左子树
BackOrder(root->left);
//打印根节点
printf("%d",root->TreeDate);
//访问右子树
BackOrder(root->right);
}
层序遍历
层序遍历有些不一样,他的顺序是把每一层走完再走下一层

我们要借助栈来实现遍历

对应的顺序是
3 8 4 2 NULL 0 1 NULL 3 NULL NULL NULL NULL
程序执行结果

总结
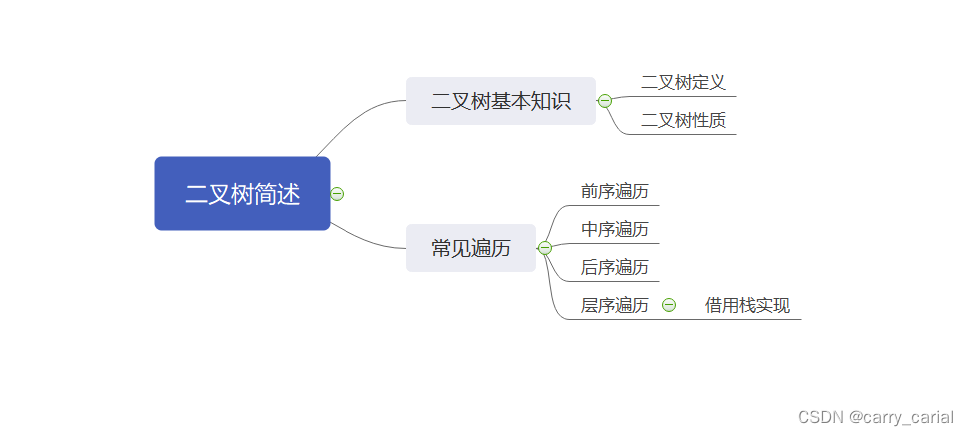
希望大家看完,能够有所收获
如果有错误,请指出我一定虚心改正
动动小手点赞
鼓励我输出更加优质的内容