文章目录
- 0.二叉树的形态和基本性质
- 1.完全二叉树的叶子节点个数
- 2.树的叶子节点个数
- 3.线索二叉树
- 4.树和森林和二叉树
- 5.平衡二叉树的最少结点数
- 6.树/二叉树/森林的转换
0.二叉树的形态和基本性质
- 一棵二叉树具有5中基本形态
- n个结点可以构造的二叉树种数: C2n-n/n+1
一棵树 n个结点
- n-1条边: 每一个结点头上都有一个边 除了根节点
- 对于二叉树 度数和 == n-1 每一条边就是一个度
- x0 = x2 + 1
- 边数 == 2x2 + x1
先根遍历和后根遍历序列完全相反
- 该树高度 == 结点数
- 该树只有一个叶子结点
对于二叉树的先/中/后根遍历
顺序完全一样 只不过根的位置不同
二叉树只有度为0和2的结点 二叉树结点个数至少为
2(h-1) + 1 : 第一层为1个 其余均为2个
二叉树的后序遍历非递归算法不使用栈
最佳方案是采用三叉链表
1.完全二叉树的叶子节点个数
- 假设
叶子节点即度为0的有n0个
度为1的节点个数为n1
度为2的节点个数为n2 - 对于二叉树:
n0+n1+n2=n
n0=n2+1
===>n0=(n+1-n1)/2 - 对于完全二叉树:
n1=0 或 1 - 总结:
n1=0或者n为奇数 ==> n0 = (n+1)/2
n1=1或者n为偶数 ==> n0 = n/2
2.树的叶子节点个数
设树T的度为4,其中度为1、2、3、4的结点个数分别为4、2、1、1。则T中有多少个叶子结点?
- n = n0 + n1 + n2 + n3 + n4 = n0 + 8
- 边数 = n - 1 且 度数和 = n - 1 ==> n = 度数和 + 1
- n = 14+22+31+41+1 = 16
- x0 == 8
3.线索二叉树
虽然在中序遍历时具有一定的优势,但也存在一些问题无法解决,包括以下几个方面:
-
插入和删除操作麻烦且速度较慢:由于线索二叉树中每个结点都需要维护前驱和后继指针,因此在插入和删除结点时需要更新这些指针,操作相对复杂且速度较慢。
-
线索子树不能共用:线索二叉树中的线索只能在某种遍历方式下使用,而不能在其他遍历方式下使用。这意味着如果需要在不同的遍历方式下使用线索,就需要对二叉树进行多次线索化,导致额外的时间和空间开销。
-
不支持动态结点的插入和删除:线索二叉树的线索化过程是在遍历过程中完成的,因此无法在遍历过程中动态地插入和删除结点。如果需要在遍历过程中动态地修改二叉树的结构,就需要重新线索化整个二叉树,效率较低。
-
需要额外的存储空间:线索二叉树中每个结点都需要维护前驱和后继指针,这会占用额外的存储空间。尤其是在结点较多的情况下,额外的存储空间开销会比较大。
综上所述,线索二叉树虽然在中序遍历时具有一定的优势,但在插入和删除操作、线索共用、动态结点修改和额外存储空间等方面存在一些问题无法解决。
不能有效解决先序线索二叉树找先序前驱和后序线索二叉树找后序后继。
4.树和森林和二叉树
- 求一个有 n 个非终端结点的森林/树对应的二叉树中右指针域为空的结点个数
n+1
- 树的先根遍历与其对应的二叉树先序遍历序列相同
- 树的后根遍历与其对应的二叉树中序遍历序列相同
对于一个有N个结点、K条边的森林,求有几棵树
假设有m棵树,第i棵树的节点数为ni ==> 第i棵树的边数为ni-1。
(n1 - 1) + … + (nm - 1) = K ⇒ N - m = K ⇒ m = N - K
5.平衡二叉树的最少结点数
F(n) = F(n-1) + F(n -2 ) + 1
F(1) = 1
F(2) = 2
F(3) = 4
F(4) = 7
最多即为满二叉树
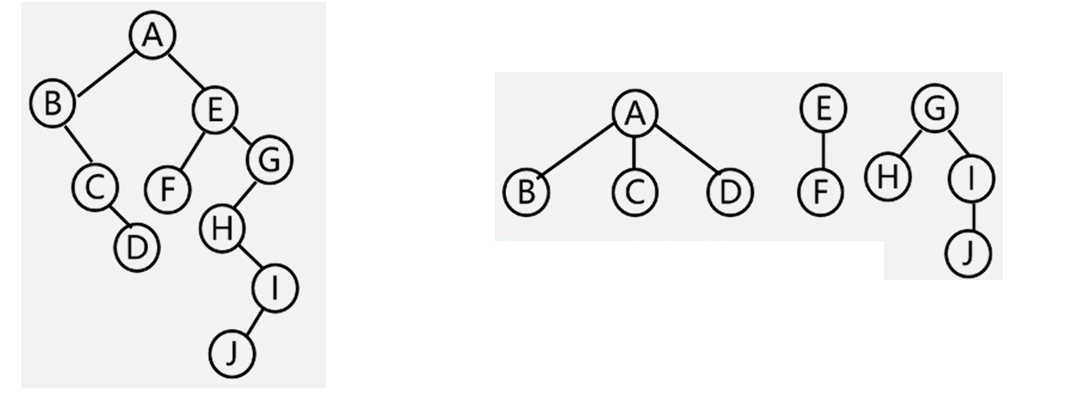
6.树/二叉树/森林的转换
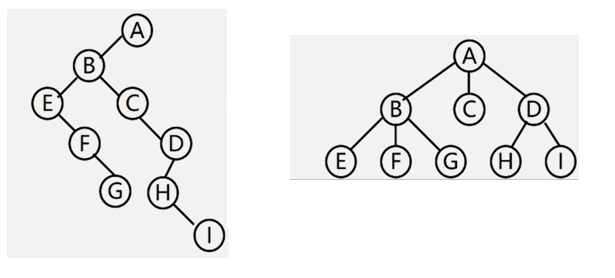
- 树变二叉树 : 兄弟相连留长子
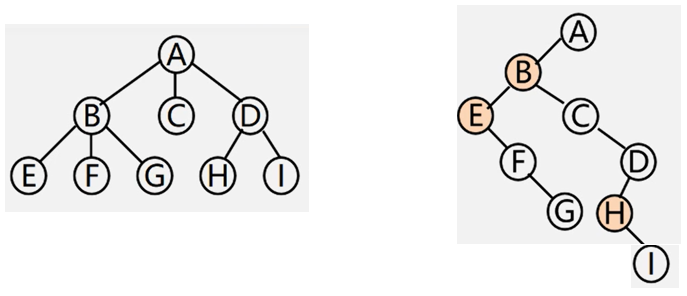
- 二叉树变树 : 左孩右右连双亲 去掉原来右孩线
- 森林变二叉树: 各个树先变成二叉树 二叉树根相连
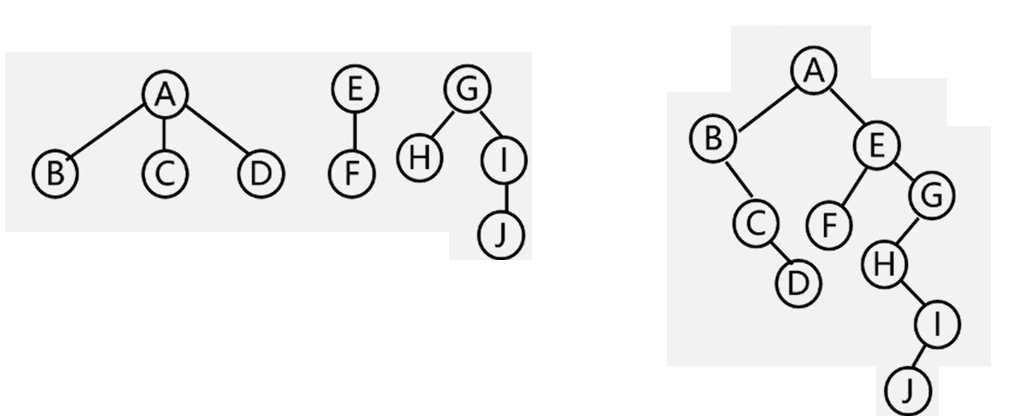
- 二叉树变森林: 根的右子树独立成根 各个二叉树变树