F题使用python,就是加了一个end = '\0',然后寄了好多。
A 猜群名
小沙为了这场元旦比赛绞尽脑汁,他现在在每个题目中藏入了一个字,收集所有的字,并将按照题号排列成一句话即可通过本题**!**
其次关于本场比赛难度预告:
输入描述:
无
输出描述:
将每个题隐藏的文字按照题号的顺序进行输出。
例如:
ABCDEFGH
首先有两个误区:
- 题目包括具体的内容而不仅仅是题目的“题目”(标题)
- 文字不一定是文字,也有可能是感叹号
对应情况:
A-> !
B-> A
C-> K
D-> 百
E-> 跨
F-> 赛
G-> 年
H-> 五
跨年五百AK赛!
print('EGHDBCFA')
B 分赃
题目描述
小沙和兰子在分赃(bushi,他们获得了一个长度为 �n 的数列 A ,他们都觉得如果一个数字自己只拥有一个,那么他是有用的,如果拥有了两个及以上那么就会变得不珍惜。
所以我们定义,对于每个人他的快乐值为他所拥有的数字中独一无二的个数。请问你能否让兰子和小沙的快乐值相等。
例如对于数列 1 2 2 3 3 3 ,小沙可以获得 1 2 3 3 ,兰子可以获得 2 3 ,他们的快乐值都为 2 。因为小沙手中独一无二的有 1 和 2 ,兰子手中独一为二的有 2 和 3 。
小沙和兰子的分赃结果中,允许有人获得的数字数目为 0 。
输入描述:
第一行输入一个整数n,代表数列的长度,1≤n≤105。
第二行输入n个整数a,1≤ai≤105。
输出描述:
如果可以相等那么输出"YES"(不带引号)
否则输出"NO"(不带引号)。
示例1
输入
6
1 2 2 3 3 3
输出
YES
首先,我们分析:
对于某一个数字,如果有一个,那么必须要分给一个人,所以必定会引起一个人的快乐值变化
如果某个数字的个数是2,如果全部给一个人,不影响快乐值,如果分给两个人,不影响快乐值的大小。
综上:出现两次的数字相当于没有出现
如果某个数字出现的次数大于等于3,那么可以给一个人分给1,另一个2,可以给一个人增加快乐值。也可以全部给一个人,使得这个数字作废。
所以:
- 对于出现一次的,如果个数是偶数,那么均分,大于等于三的(有的话)全部给一个人。
- 对于出现一次的,如果个数是奇数,均分,显然一个人的比另一个人的数字多一。
如果有大于等于三的,那么可以填补平。
如果没有,就寄了。
#include <bits/stdc++.h>
using namespace std;
#define N 100200
int n;
int a[N];
int f[N];
int cnt[N];
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", a+i);
}
for(int i =1; i <= n; i++){
f[a[i]]++;
}
int n1 = 0, n2 = 0, n3 = 0;
for(int i = 1; i <= 1e5; i++){
if(f[i] == 1) n1++;
else if(f[i] >= 3) n2 ++;
//else if(f[i] >= 4) n3 ++;
}
if(n2) puts("YES");
else{
if((n1)%2){
puts("NO");
}
else{
puts("YES");
}
}
return 0;
}
C 翻卡牌
小沙有9张扑克牌,上面分别有 A23456789 各一张,没有 10JQK 。其中 A 我们使其为数字 1 ,下文也皆由数字 1 表示。现在小沙将其打乱,排列至一排,全部背置。
小沙手里有一个神秘的魔法,可以对于这九张扑克牌从前往后拼成的九位数,会将其复制一份前后拼接成一个十八位数字,然后获得该数字对 7 取模之后的金币数。
例如小沙手上的扑克牌全部翻开之后为 2 5 4 3 6 7 1 9 8,拼接之后的九位数为 254367198 ,复制一份之后为 254367198254367198 ,对7取模之后为 0,所以小沙无法获得金币。
现在小沙将问题抛给你,小沙会翻开几张(可能是 0 )扑克牌,剩下几张扑克牌仍处于背置状态。小沙想你帮他算一下,剩下的所有可能出现的情况中,小沙赚金币的期望是多少。

输入描述:
输出一行长度为9的字符串,其中仅包括数字1到9,和字符?。其中?代表该位置未翻开。
输出描述:
输出一个整数代表答案。
输入
254367?9?
输出
0
说明
无论结果是 254367198还是254367891他们获得的金币都是0个。
这一道题目可以使用暴力:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll a[15];
char s[20];
const int mod = 1e9+7;
bool ck()
{
for(int i = 1; i <= 9; i++){
if(s[i] != '?' && (ll)a[i] + '0' != (ll)s[i]) return false;
}
return true;
}
ll ksm(ll a, ll b){
ll ret = 1;
while(b){
if(b & 1) ret = ret * a % mod;
a = a * a % mod;
b >>= 1;
}
return ret;
}
int main()
{
ll cnt = 0;
ll ans = 0;
for(int i = 1; i <= 9; i++){
a[i] = i;
}
scanf("%d", s+1);
do{
if(!ck()) continue;
ll tmp = 0;
for(int i = 1; i <= 9; i++) tmp = tmp * 10 + a[i];
for(int i = 1; i <= 9; i++) tmp = tmp * 10 + a[i];
cnt ++;
ans = (ans + tmp) % mod;
}while(next_permutation(a+1, a+9+1));
printf("%lld", ksm(ans, mod - 2));
return 0;
}
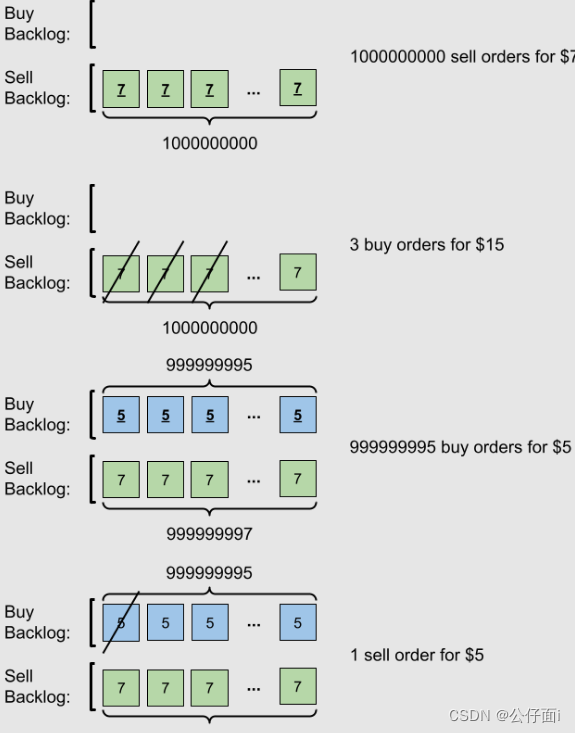
但是官方的题解中,复制一遍相当于乘以1000000001,而有 1000000001 / 7 = 142 , 857 , 143 1000000001/7 = 142,857,143 1000000001/7=142,857,143可以整除。所以最终的答案一定是0
print(0)
D ygg的分数运算

示例1
输入
2 3 18
输出
YES
输入
3 5 10
输出
NO
在这一道题目中,
1 a + 1 b = a + b a × b \frac{1}{a} + \frac{1}{b} = \frac{a + b}{a\times b} a1+b1=a×ba+b
1 a × 1 b = 1 a × b \frac{1}{a} \times \frac{1}{b} = \frac{1}{a\times b} a1×b1=a×b1
在相加的过程中,可能会产生约分,但是分母是可以表示为两个素数的乘积,所以无伤大雅,约分之后还是这两个素数某次方的乘积。
所以仅仅使用乘法运算所得到的情况等价于使用两种运算得到的情况。
在这里我顿时想起了《NOJ.加一乘二平方》,使用了伟大的《分支限界法》,暴力枚举了经过若干次乘法的所有情况。
#include <bits/stdc++.h>
using namespace std;
#define int long long
int a, b, c;
queue<int> q;
map<int, bool> vis;
bool bfs()
{
q.push(a);
q.push(b);
vis[a] = 1;
vis[b] = 1;
if(a == c || b == c) return true;
while(q.size()){
int t = q.front();
q.pop();
int nx = t * a;
if(nx <= 1e9)
{
if(!vis[nx]){
q.push(nx);
vis[nx] = 1;
}
if(nx == c) return true;
}
nx = t * b;
if(nx <= 1e9)
{
if(!vis[nx]){
q.push(nx);
vis[nx] = 1;
}
if(nx == c) return true;
}
}
return false;
}
signed main()
{
scanf("%lld%lld%lld", &a, &b, &c);
if(bfs()){
puts("YES");
}
else{
puts("NO");
}
return 0;
}
但是在这里,好像仅仅用c除以a,b看余数是不是等于0就可以了
#include <bits/stdc++.h>
using namespace std;
int main()
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
while(c % a == 0) c /= a;
while(c % b == 0) c /= b;
if(c == 1)puts("YES");
else puts("NO");
return 0;
}
EFG
由于太水,不做题解
H nana吃蛋糕
题目描述
nana有一天肚子很饿,呜五呜,很想吃蛋糕,她进入了一个边长大小为 n 的蛋糕正方形方阵,每一个矩阵方格上面都会放置一些蛋糕,我们规定( x , y )代表矩阵的第 x 行第 y 列,nana出发的起点为( 1 , 1 ),终点为( n , n )。
她遵循以下四种行走方式,同时她每个格子只能走一次:
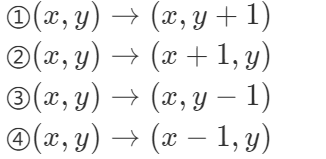
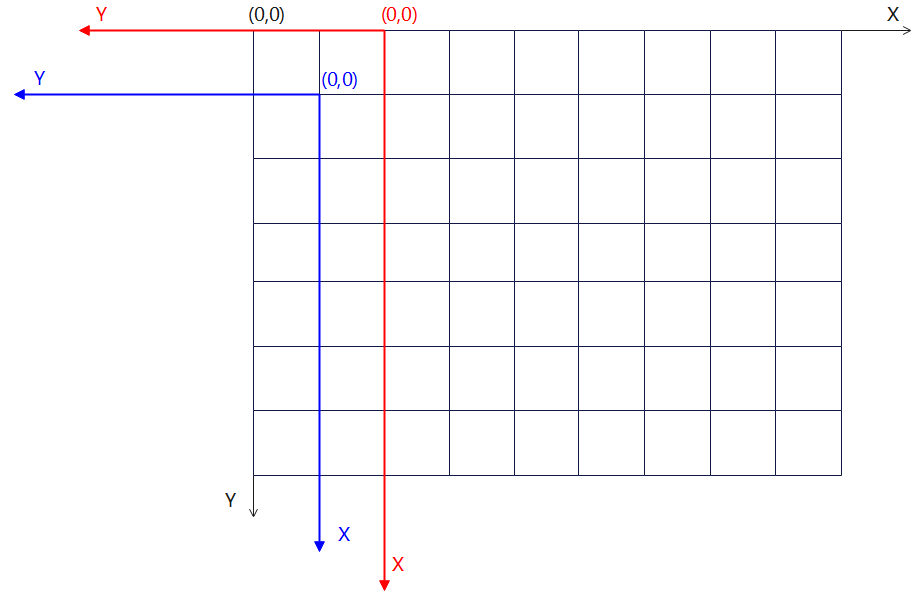
如果该行走方式会跨越边界,那么nana会从另一边出现。
例如:
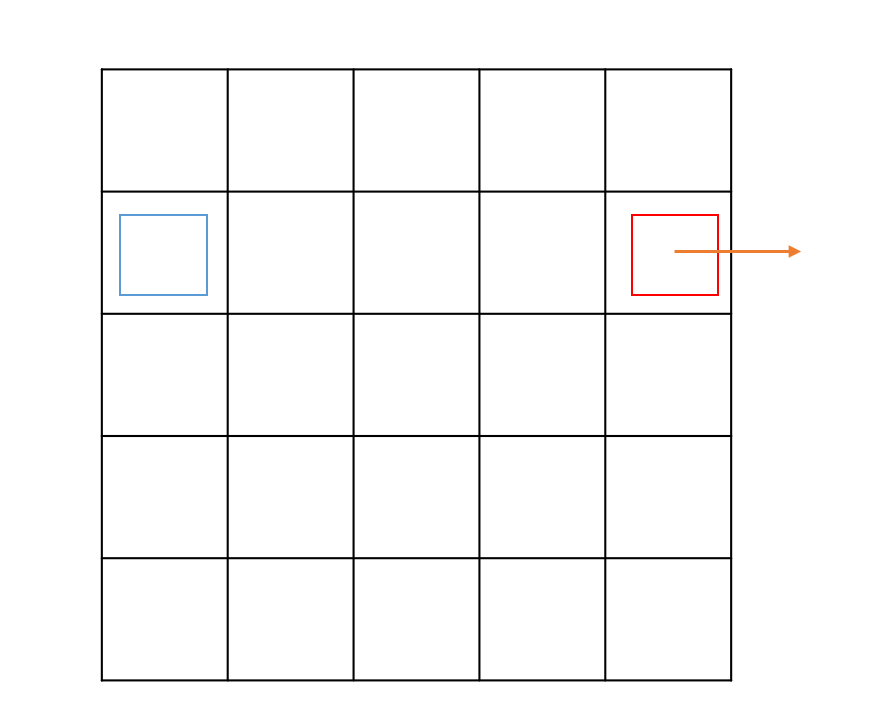
红色地点向右行走会到达蓝色地点。
上下边界同理。
问nana最多能吃到多少蛋糕🎂?
输入描述
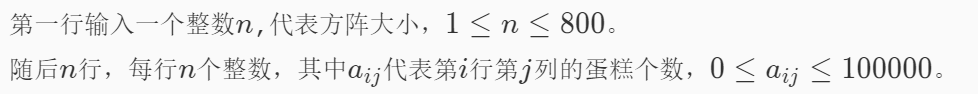
输出描述:
输出一个整数代表答案,代表nana最多能吃到的蛋糕个数。
输入
2
1 1
1 1
输出
3
题解
官方题解:Click_here
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define N 820
int a[N][N];
signed main()
{
int n;
scanf("%lld", &n);
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= n; j++){
scanf("%lld", &a[i][j]);
}
}
int sum = 0;
int minv = 0x7f7f7f7f;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
sum += a[i][j];
if((i&1)^(j&1)){
minv = min(minv, a[i][j]);
}
}
}
if(n & 1){
printf("%lld", sum);
}
else{
printf("%lld", sum - minv);
//cout << endl << sum << " " << minv;
}
return 0;
}






![软件测试[用例篇]](https://img-blog.csdnimg.cn/ce621eb43873426380294dd1f2d61d8e.png)