目录
1. 什么是决策树?
2. 决策树的原理
2.1 如何构建决策树?
2.2 构建决策树的数据算法
2.2.1 信息熵
2.2.2 ID3算法
2.2.2.1 信息的定义
2.2.2.2 信息增益
2.2.2.3 ID3算法举例
2.2.2.4 ID3算法优缺点
2.2.3 C4.5算法
2.2.3.1 C4.5算法举例
2.2.4 CART算法
2.2.4.1 Gini指数(基尼指数)
2.2.4.2 Cart算法 相关公式
2.2.4.3 Cart算法举例
3. 未完待续。。。
4. 本文涉及的代码
1. 什么是决策树?
决策树分类的思想类似于找对象。
想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女孩决定是否见男孩的一个过程,就像一个树形结构,只不过是反正的树, 数学上或者机器学习里的树,根在最上方
最上方的为树的根节点,下面的都是子节点
像下图的橙色的部分,下面在没有往下的结点的叫叶子节点
如果一颗树每个节点下面最多只有两个节点就属于二叉树
下图的就是一个非二叉树( 到收入下面有三个节点)
上图完整表达了这个女孩决定是否见一个约会对象的策略,
其中绿色节点表示判断条件,
橙色节点表示决策结果,
箭头表示在一个判断条件在不同情况下的决策路径,
图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,
如果将所有条件量化,则就变成真正的决策树了。
有了上面直观的认识,我们可以正式定义决策树了:决策树(decision tree)是一个树结构(可以是二叉树或非二叉树)。
其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。
使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节
点,将叶子节点存放的类别作为决策结果可以看到,决策树的决策过程非常直观,容易被人理解。目前决策树已经成功运用于医学、制造产业、天文学、分支
生物学以及商业等诸多领域。决策树的主要优势就在于数据形式非常容易理解。决策树算法能够读取数据集合,构建类似于上面的决策树,决策树很多任务都是为了数据中所蕴含的知识信息,因此决策树可以使用不熟悉的数据集合,并从中提取出一系列规则,机器学习算法最终将使用这些机器从数据集中创造的规则。专家系统中经常使用决策树,而且决策树给出结果往往可以匹敌在当前领域具有几十年工作经验的人类专家
2. 决策树的原理
2.1 如何构建决策树?
首先,例如上方的图,我们可以分析到,我们要先选择 判断条件,
例如有些女孩找男朋友的第一个条件考虑年龄而有的考虑收入有的还考虑长相等等,所以这就是构造决策树的第一个关键的点:判断条件的顺序,
有了判断条件之后,怎么判断这个节点的分裂,例如,年龄这个判断条件,是按照30岁分还是按照什么分,符合这个条件是一个节点,不符合这个判断条件的是另外一个节点,这就是构造决策树的第二个关键的点:节点分裂的界限或者说节点分裂的定义和分类
构造决策树关键步骤是分裂属性,所谓分裂属性就是在某个节点处,按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能的“纯”,尽可能“纯” 就是尽量让一个分裂子集中待分类项属于同一类别
2.2 构建决策树的数据算法
2.2.1 信息熵
有了刚说的两个关键点,对于这个两个关键点的选择就有点困难,所以需要具体的算法来做
建决策树的数据算法有很多
ID3算法
C4.5算法
CART算法
.....
等等
这里面就牵扯了信息论中的信息熵 有关信息熵可参考(可以点开全部回答,然后搜索 阅读 ,或者自行查看 )
信息熵是什么? - 知乎原创文章,一家之言。转载请注明出处。个人公众号:follow_bobo机器学习入门:重要的概念---信息熵(Shan…
https://www.zhihu.com/question/22178202/answer/265757803
信息熵的数学公式:
2.2.2 ID3算法
ID3算法算的是信息增益
2.2.2.1 信息的定义
熵定义为信息的期望值,在明确这个概念之前,我们必须知道信息的定义,如果待分类的事务划分在多个分类之中,则符合X的信息定义为:
其中p(x)是选择该分类的概率
为了计算熵,我们需要计算所有类别所有可能的信息期望值,通过下面的公式得到:
其中n 是分类的数目
在决策树当中,设D为用类别对训练元组进行的划分,则D的熵(entropy)表示为:
其中pi 表示第i个类别在整个训练元组出现的概率,可以用属于此类别元素的数量除以训练元组元素总数作为估计。
熵的实际意义表示是D中元组的类标号所需要的平均信息量
现在我们假设将训练元组D按属性A进行划分,则A对D划分的期望信息为:
2.2.2.2 信息增益
ID3算法 利用 信息增益来决定优先使用哪个特征进行分裂
先用没有进行任何属性分类的时候,计算一个信息熵
再选其中的某一个特征进行分裂构造决策树,再计算一个信息熵,具体用哪个特征来计算,要看哪个特征计算出来的信息熵大,就用哪个,因为这样算出来的值越大相减之后就消除了原来数据里面最大的不确定性
这两个信息熵之间会有一个差值, 这两个信息熵之差,得到的值叫做信息增益
2.2.2.3 ID3算法举例
ID3算法就是在每次需要分裂时,计算每个属性的增益率,然后选择增益率最大的属性进行分裂,
如下图假设训练集合包含10条数据,预测一下,社交网站上的账号是否真实的账号
根据日志密度,好友密度,是否使用真是头像等(这些都为特征)来预测
代表的含义: s 小,m中等,l 大
先完成构建决策树其中一个关键点:首先用那个特征进行分裂
计算思路:
1⃣️ 先计算没有使用任何特征对账号是否真实的计算的信息熵
2⃣️ 再算随便使用一个特征对账号是否真实的计算的信息熵
代码如下:(使用 jupyter notebook)
import pandas as pd import numpy as np# 计算图中的信息熵,确定一个分类的特征 # D 就是我们的原始数据 # 先计算未使用任何特征的进行分类的信息熵(所以只需关心账号是否真实这一列) # 账号是否真实: 有两种情况,分别为 yes no, yes数量为7(概率为0.7),no的数量为3(概率为0.3) # 根据信息熵公式: info_D = -(0.7 * np.log2(0.7) + 0.3 * np.log2(0.3)) info_D # 0.8812908992306927使用 日志密度 对账号是否真实的信息熵
使用公式# 使用 日志密度 对账号是否真实的信息熵 使用公式 # j 就是 3(因为日志密度有三种情况,s,l,m) # s 三个(0.3),对应账号是否真实列,2个no, 1个yes # l 三个(0.3), 对应账号是否真实列,0个no, 3个yes # m 四个(0.4), 对应账号是否真实列,1个no, 3个yes # s情况中对日志密度划分的信息熵 = s 的 概率 ✖️ s 中对账号是否真实的信息熵 = 0.3 * ((-1/3) * np.log2(1/2) + (-2/3) * np.log2(2/3)) # 同理 l = 0.3 * (-1 * log2(1)) # 同理 m = info_D_Log = 0.3 * ((-1/3) * np.log2(1/3) + (-2/3) * np.log2(2/3)) + 0.3 * (-1 * np.log2(1)) + 0.4 * ((-1/4) * np.log2(1/4) + (-3/4) * np.log2(3/4)) info_D_Log# 使用 日志密度 进行划分的信息增益 info_D - info_D_Log # 0.2812908992306927# 使用 好友密度 对账号是否真实的信息熵 # s 4个(0.4),对应账号是否真实列,3个no, 1个yes # m 4个(0.4), 对应账号是否真实列,0个no, 4个yes # l 2个(0.2), 对应账号是否真实列,0个no, 2个yes info_D_F = 0.4 * ((-3/4) * np.log2(3/4) + (-1/4) * np.log2(1/4)) + 0 + 0 info_D_F # 0.32451124978365314# 使用 好友密度 进行划分的信息增益 info_D - info_D_F # 0.5567796494470396# 使用 是否使用真实头像 对账号是否真实的信息熵 # no 5个 2个no,3个yes # yes 5个 1个no,4个yes info_D_H = 0.5 * ((-2/5) * np.log2(2/5) + (-3/5) * np.log2(3/5)) + 0.5 * ((-1/5) * np.log2(1/5) + (-4/5) * np.log2(4/5)) info_D_H # 0.8464393446710154# 使用 是否使用真实头像 进行划分的信息增益 info_D - info_D_H # 0.034851554559677256根据上述的运算结果,可以看到, 使用 好友密度 进行划分的信息增益 的 值最大 ,所以 我们就用好友密度这个特征来构建决策树
再完成构建决策树另外一个关键点:首先用那个特征进行分裂节点分裂的界限或者说节点分裂的定义和分类, 而这些我们不需要关心,ID3算法会帮我们做好,只要能确定出来用哪个特征即可
分裂属性分为三种不同的情况:
- 属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
- 属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
- 属性是连续值。此时确定一个值作为分裂点split_point,
按照>split_point和<=split_points生成两个分支。离散值即 例子中的 s,m,l,这种就是有三个划分,而连续值类似年龄这种连续值,29,30,31等
2.2.2.4 ID3算法优缺点
- 优点:简单、时间复杂度、时间复杂度都不高
- 缺点:数据中大量的离散型的数据,会对分裂造成误差
2.2.3 C4.5算法
因为ID3算法在对于离散型特征的处理不好,引入C4.5算法
C4.5算法,计算的是信息增益率
计算步骤:
- 先计算信息增益
- 再除以这个特征本身的信息熵
2.2.3.1 C4.5算法举例
信息增益,上面ID3算法已经计算出来,可以直接使用, 代码如下
2.2.4 CART算法
2.2.4.1 Gini指数(基尼指数)
由上面的内容我们已经知道,决策树的核心就是寻找纯净的划分,因此引入了纯度的概念。在属性选择上,我们是通过统计“不纯度”来做判断的,ID3 是基于信息增益做判断,C4.5 在 ID3 的基础上做了改进,提出了信息增益率的概念。实际上 CART 分类树与 C4.5 算法类似,只是属性选择的指标采用的是基尼指数。
基尼指数本身反应了样本的不确定度。当基尼系数越小的时候,说明样本之间的差异性小,不确定程度低。分类的过程本身是一个不确定度降低的过程,即纯度的提升过程。所以 CART 算法在构造分类树的时候,会选择基尼系数最小的属性作为属性的划分。
在决策树Cart算法中用Gini指数来衡量数据的不纯度或者不确定性
2.2.4.2 Cart算法 相关公式
在分类问题中,样本属于第 i 类的概率为
经过特征a分割之后集合D的不确定性,基尼指数越大,不确定性越大,因此我们需要寻找基尼指数越小的特征作为节点
2.2.4.3 Cart算法举例
3. 本文涉及的代码
https://download.csdn.net/download/wei18791957243/88660903
https://download.csdn.net/download/wei18791957243/88660903https://download.csdn.net/download/wei18791957243/88660904
https://download.csdn.net/download/wei18791957243/88660904
https://download.csdn.net/download/wei18791957243/88664136
https://download.csdn.net/download/wei18791957243/88664136
1.决策树
news2026/2/15 0:38:18
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1337132.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
智能优化算法应用:基于孔雀算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于孔雀算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于孔雀算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.孔雀算法4.实验参数设定5.算法结果6.参考文献7.MA…
机械革命极光Pro重装Win10系统图解
机械革命极光Pro是性能优秀的笔记本电脑,深受广大用户的喜欢,现在用户想给笔记本电脑重新安装一下操作系统,但不知道重装系统的详细步骤。下面小编将带来机械革命极光Pro笔记本电脑重装系统Win10版本的步骤介绍,帮助更多的用户完成…
Python 基础面试第三弹
1. 获取当前目录下所有文件名 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import os def get_all_files(directory): file_list []<br> # <code>os.walk</code>返回一个生成器,每次迭代时返回当前目录路径、子目录列表和文件列表 for…
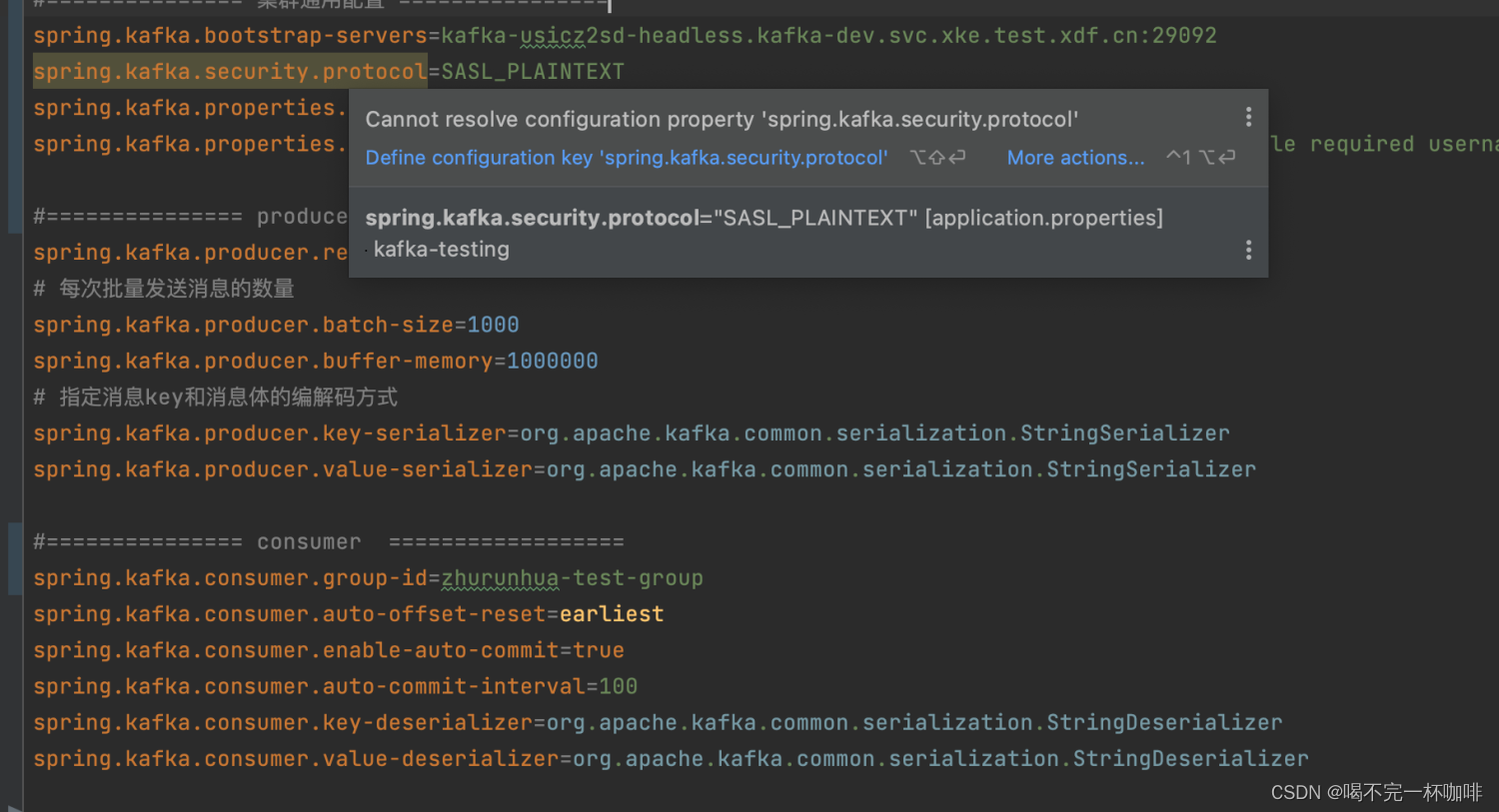
【Kafka】Kafka客户端认证失败:Cluster authorization failed.
背景
kafka客户端是公司内部基于spring-kafka封装的spring-boot版本:3.xspring-kafka版本:2.1.11.RELEASE集群认证方式:SASL_PLAINTEXT/SCRAM-SHA-512经过多年的经验,以及实际验证,配置是没问题的,但是业务…
数据结构:图文详解 树与二叉树(树与二叉树的概念和性质,存储,遍历)
目录
一.树的概念
二.树中重要的概念
三.二叉树的概念
满二叉树
完全二叉树
四.二叉树的性质
五.二叉树的存储
六.二叉树的遍历
前序遍历
中序遍历
后序遍历 一.树的概念 树是一种非线性数据结构,它由节点和边组成。树的每个节点可以有零个或多个子节点…
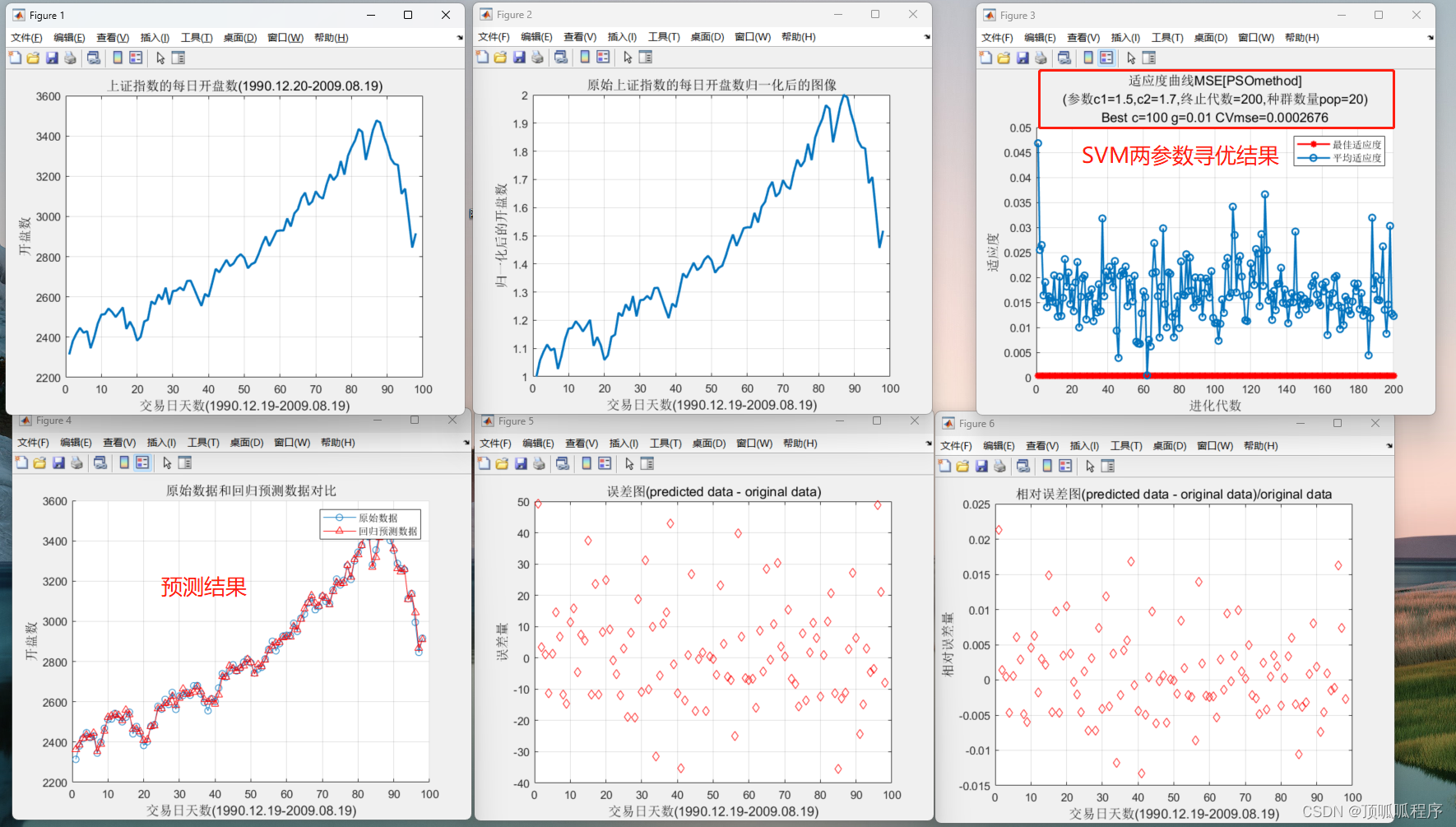
113基于matlab的PSO-SVM多输入单输出预测程序
基于matlab的PSO-SVM多输入单输出预测程序。PSO对SVM的两个参数进行优化得到最佳参数值进行预测。并输出预测误差等相应结果。程序已调通,可直接运行。 113matlabPSO-SVM多输入单输出 (xiaohongshu.com)
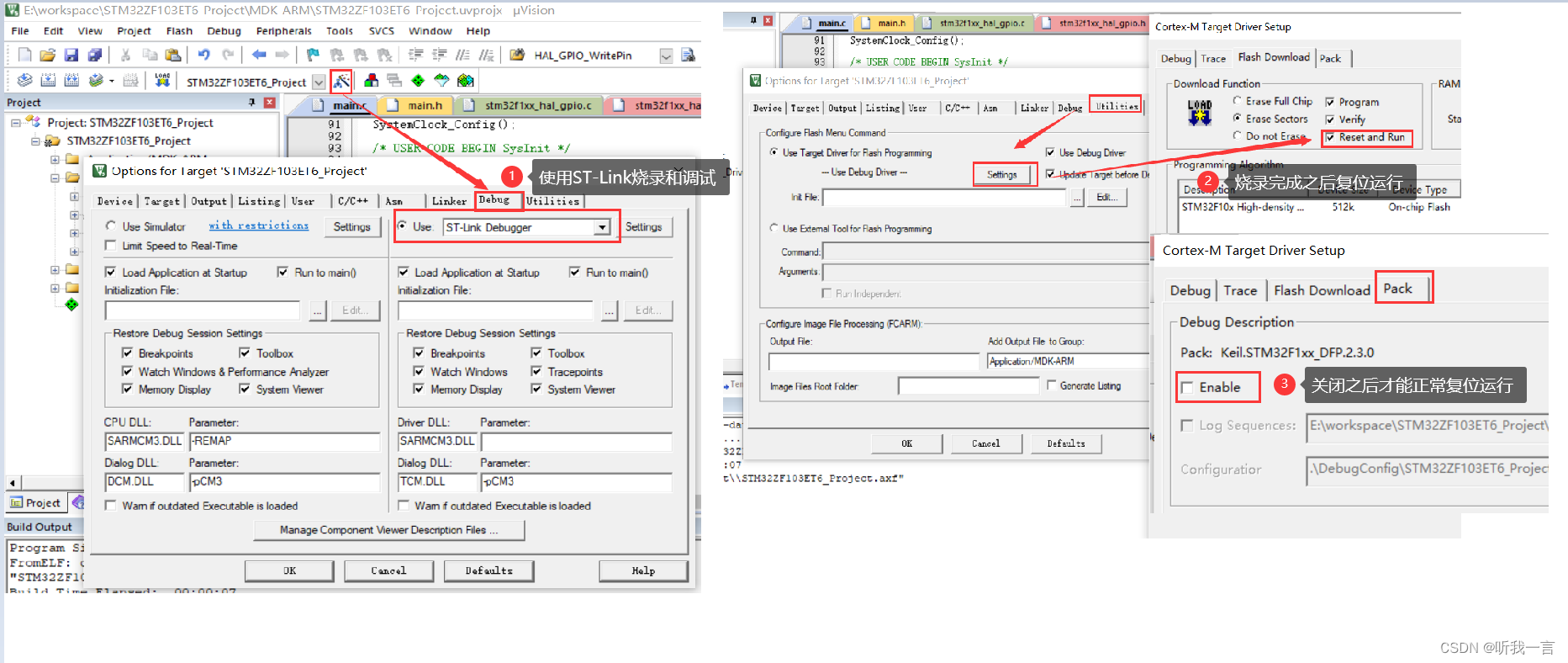
普中STM32-PZ6806L开发板(STM32CubeMX创建项目并点亮LED灯)
简介
搭建一个用于驱动 STM32F103ZET6 GPIO点亮LED灯的任务;电路原理图
LED电路原理图 芯片引脚连接LED驱动引脚原理图
创建一个点亮LED灯的Keil 5项目
创建STM32CubeMX项目
New Project -> 单击 -> 芯片搜索STM32F103ZET6->双击创建
初始化时钟 初始化LED G…
基于双闭环PI的SMO无速度控制系统simulink建模与仿真
目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
5.完整工程文件 1.课题概述 基于双闭环PI的SMO无速度控制系统simulink建模与仿真,基于双闭环PI的SMO无速度控制系统主要由两个闭环组成:一个是电流环,另一个是速度环。…
Flink CDC 1.0至3.0回忆录
Flink CDC 1.0至3.0回忆录 一、引言二、CDC概述三、Flink CDC 1.0:扬帆起航3.1 架构设计3.2 版本痛点 四、Flink CDC 2.0:成长突破4.1 DBlog 无锁算法4.2 FLIP-27 架构实现4.3 整体流程 五、Flink CDC 3.0:应运而生六、Flink CDC 的影响和价值…
数据库原理及应用·数据库保护
7.1 事务
7.1.1 事务定义
1.事务是用户定义的一个数据操作序列,这些操作要么全部执行、要么全部不执行,是一个不可分割的工作单元。
事务是恢复和并发控制的基本单位
事务的两种方式:
7.1.2 事务处理模型
1.ISO事务处理模型:…
隐私第一:在几分钟内部署本地大语言模型!
彻底改变您的数据安全游戏:快速无缝部署本地大语言模型,实现无与伦比的隐私! 2023年是人工智能领域加速发展的一年。除了健壮的商业上可用的大型语言模型之外,还出现了许多值得称赞的开源方案,例如Llama2、Codellama、Mistral和Vi…
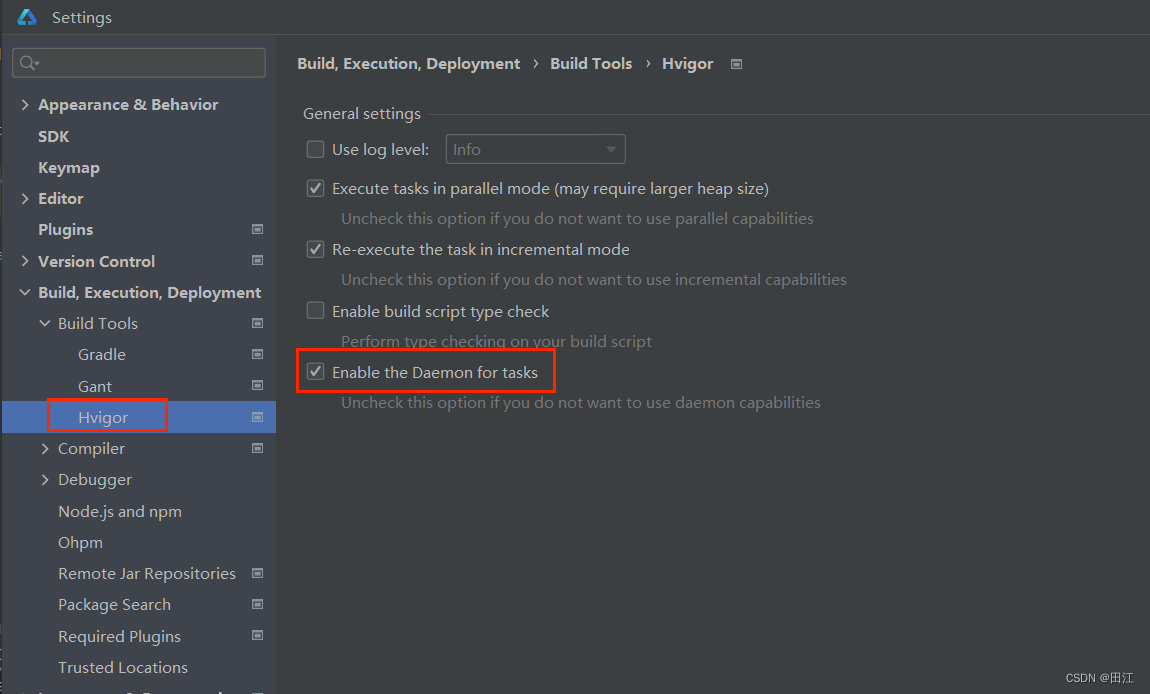
鸿蒙开发中的坑(持续更新……)
最近在使用鸿蒙开发时,碰到了一些坑,特做记录,如:鸿蒙的preview不能预览,轮播图组件Swiper使用时的问题,console.log() 打印的内容 一、鸿蒙的preview不能预览
首先,只有 ets文件才能预览。
其…
HarmonyOS应用抓包实战
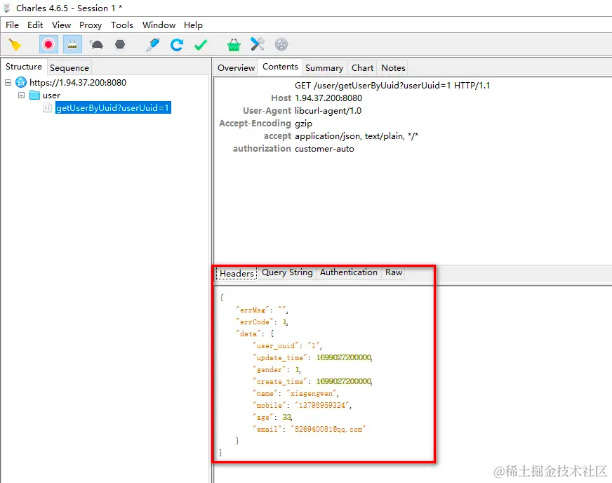
Charles抓包原理
Charles是一个HTTP代理服务器,HTTP监视器,反转代理服务器,当浏览器连接Charles的代理访问互联网时,Charles可以监控浏览器发送和接收的所有数据。
在开发OpenHarmony/HarmonyOS应用开发时,我们使用的是ohos/axios来进行网络…
2023.12.25 关于 Redis 数据类型 Hash 常用命令、内部编码、应用场景
目录
Hash 数据类型
Hash 操作命令
HSET
HGET
HEXISTS
HDEL
HKEYS
HVALS
HGETALL
HMGET
HLEN
HSETNX
HINCRBY
HINCRBYFLOAT
HSTRLEN
Hash 编码方式
理解什么是压缩
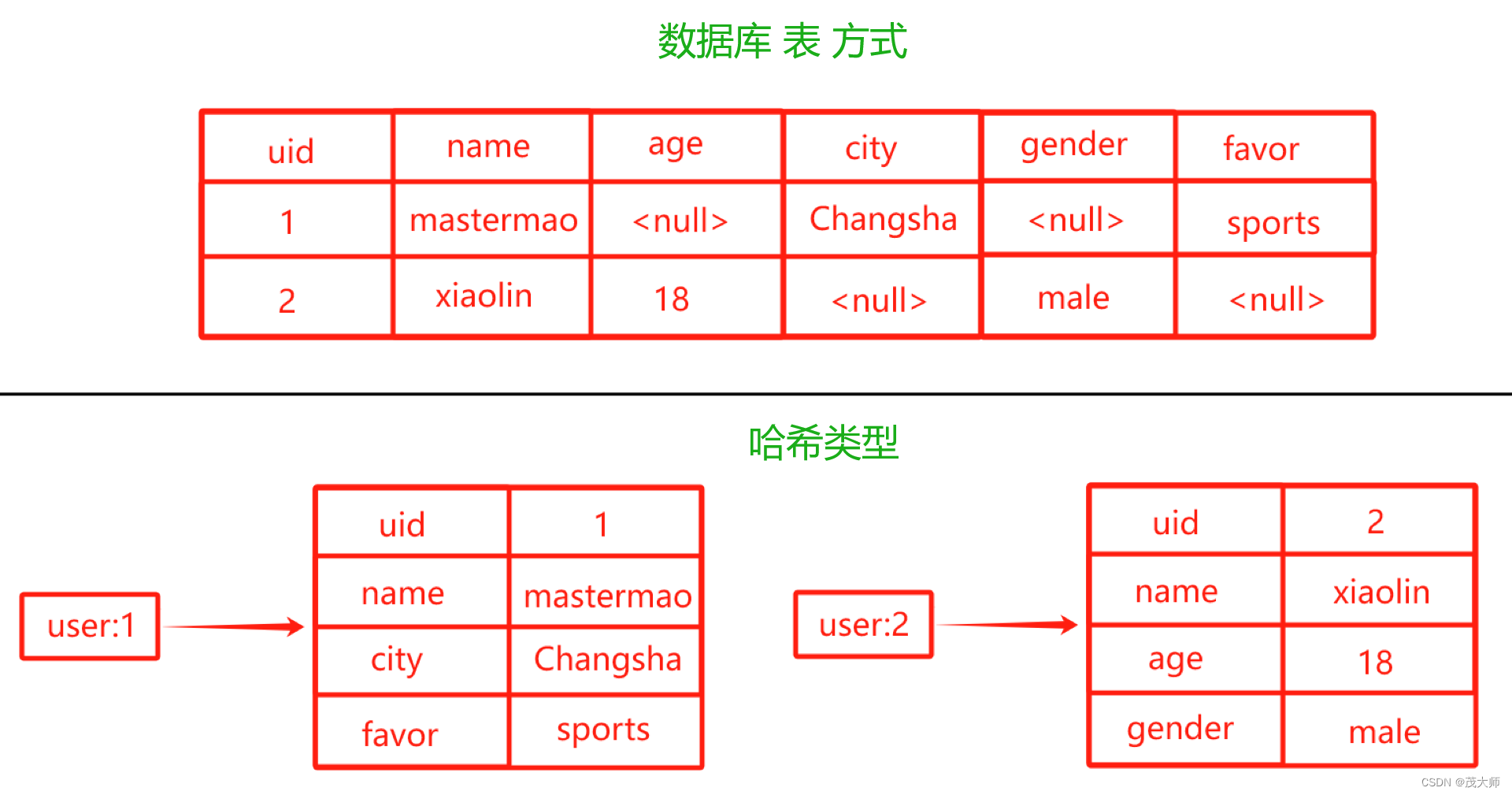
Hash 实际应用
Cache 缓存 Hash 数据类型 整体上来说 Redis 是键值对结构,其中 …
基于JSP+Servlet+Mysql的学生宿舍管理系统(简单的增删改查)
基于JSPServletMysql的学生宿舍管理系统 一、系统介绍二、功能展示1.登陆、注册2.主页3.增加3.修改4.删除 四、其它1.其他系统实现五.获取源码 一、系统介绍
项目名称:基于JSPServletMysql的学生宿舍管理系统(简单的增删改查)
项目架构:B/S架构
开发语…
电视盒子什么品牌好?经销商分享线下热销电视盒子排行榜
做实体数码店已经超过六年了,我对电视盒子这行是非常了解的,品牌的优势和特色都有研究,超级多网友在讨论电视盒子什么品牌好,我整理了店铺内销量最高的电视盒子排行榜,想知道目前哪些电视盒子最受消费者欢迎࿰…
真实案例扫描APP开发——基于实例分割实现拍照文档实时边缘检测(C++/JNI实现)
前言
这是一个安卓NDK的项目,想要实现的效果就是拍照扫描,这里只涉及到的只有边缘检测,之后会写文档滤镜、证件识别与证件1比1打印,OCR、版面分析之后的文档还原。我的开发环境是Android Studio 北极狐,真机是华为mat…
详解Keras3.0 Layer API: LSTM layer
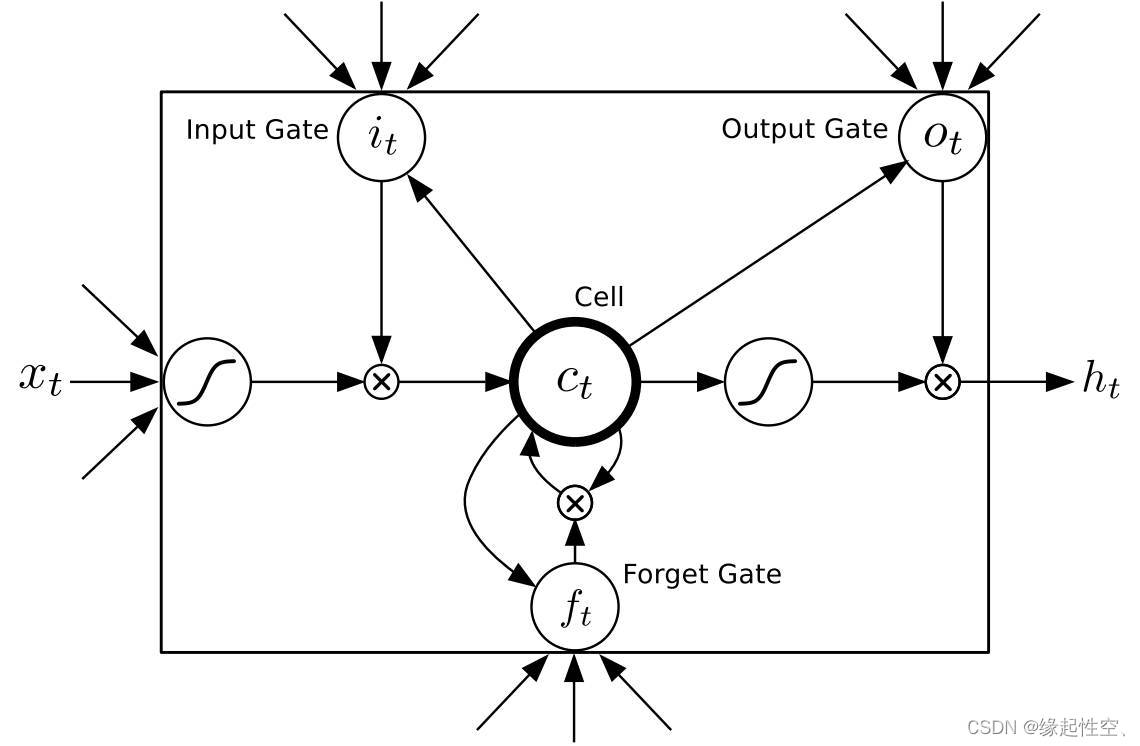
LSTM layer
用于实现长短时记忆网络,它的主要作用是对序列数据进行建模和预测。 遗忘门(Forget Gate):根据当前输入和上一个时间步的隐藏状态,计算遗忘门的值。遗忘门的作用是控制哪些信息应该被遗忘,哪些…
最新版手机无人直播硬改虚拟摄像头,支持多平台修改手机摄像头【硬改神器+使用教程】
最新版手机无人直播助手App安卓版介绍:
顺哥轻创V:shundazy1
这是一款兼容性强大的手机无人直播工具,是无人直播神器,不依赖电脑,手机无需root权限,不需要装xp框架,支持主流平台兼容性极佳,1V…
BEECMS靶场 -->漏洞挖掘
这几天,一天一个靶场(累鼠我啦),哈哈哈,也算是积累了不少经验,今天,我们就来讲一下BEECMS靶场吧!!! 先是直接进入到他的界面…