动态规划

动态规划就像是解决问题的一种策略，它可以帮助我们更高效地找到问题的解决方案。这个策略的核心思想就是将问题分解为一系列的小问题，并将每个小问题的解保存起来。这样，当我们需要解决原始问题的时候，我们就可以直接利用已经计算好的小问题的解，而不需要重复计算。

动态规划与数学归纳法思想上十分相似。

数学归纳法：

1. 基础步骤（base case）：首先证明命题在最小的基础情况下成立。通常这是一个较简单的情况，可以直接验证命题是否成立。

2. 归纳步骤（inductive step）：假设命题在某个情况下成立，然后证明在下一个情况下也成立。这个证明可以通过推理推断出结论或使用一些已知的规律来得到。

通过反复迭代归纳步骤，我们可以推导出命题在所有情况下成立的结论。

动态规划：

1. 状态表示：

2. 状态转移方程：

3. 初始化：

4. 填表顺序：

5. 返回值：

数学归纳法的基础步骤相当于动态规划中初始化步骤。

数学归纳法的归纳步骤相当于动态规划中推导状态转移方程。

动态规划的思想和数学归纳法思想类似。

在动态规划中，首先得到状态在最小的基础情况下的值，然后通过状态转移方程，得到下一个状态的值，反复迭代，最终得到我们期望的状态下的值。

接下来我们通过三道例题，深入理解动态规划思想，以及实现动态规划的具体步骤。

714. 买卖股票的最佳时机含手续费

题目解析

状态表示

题目要求我们求利润的最大值，如果我们定义dp[i]表示，从第0天到第i天所能获得的最大利润，我们想一想能不能推导出状态转移方程？如果我们要推导出第i天的状态，仅依靠第i-1的状态是得不出来的，因为我们考虑第i天的最大利润时，需要考虑两种情况，要么第i天结束的时候，我们手上有股票，要么第i天结束的时候我们手上没有股票，这两种情况分别推导，又需要用到第i-1天的这两种情况的最大利润值。

所有我们继续将状态细分。

定义dp[i][j]（j=0或1，0表示手上有股票，1表示手上没股票）

dp[i][j]表示第i天结束的时候拥有j状态时所能获得的最大利润。

状态转移方程

我们想一想能不能由其他的状态推导出第i天的两个状态？

dp[i][0]表示第i天结束的时候手上有股票时所能获得的最大利润。

dp[i][1]表示第i天结束的时候手上没有股票时所能获得的最大利润。

dp[i-1][0]表示第i-1天结束的时候手上有股票时所能获得的最大利润。

dp[i-1][1]表示第i-1天结束的时候手上没有股票时所能获得的最大利润。

当第i天结束的时候手上有股票时，对应dp[i][0]，第i-1天结束时手上要么有股票，然后第i天白天没有把他卖掉，要么第i-1天结束时手上没有股票，然后第i天白天我们买了股票。

所以第i天结束时手上有股票时所能获得的最大利润是这两种情况下所能获得的最大利润。

很容易得到dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);

因为我们一笔交易只需要花费一次手续费，所以我们只要选择在买入股票的时候或者卖出股票的时候减去手续费就行，这里我们选择在卖出股票的时候减去手续费，所以买入的时候没有影响。

当第i天结束的时候手上没有股票时，对应dp[i][1]，第i-1天结束时手上要么有股票，然后第i天白天卖出股票，要么第i-1天结束时手上没股票，然后第i天什么也不做。

所以第i天结束时手上有股票时所能获得的最大利润是这两种情况下所能获得的最大利润。

很容易得，dp[i][1]=fmax(dp[i-1][0]+prices[i]-fee,dp[i-1][1]);

故状态转移方程为，

dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]); dp[i][1]=fmax(dp[i-1][0]+prices[i]-fee,dp[i-1][1]);

初始化

根据状态转移方程我们知道，想要推导出第i天的状态，我们需要利用第i-1天的状态。

所以我们需要初始化第0天的状态值。

由状态表示，dp[i][j]（j=0或1，0表示手上有股票，1表示手上没股票）

dp[i][j]表示第i天结束的时候拥有j状态时所能获得的最大利润。

dp[0][0]表示第0天结束时，手上有股票，说明第0天白天买了股票，利润为-prices[0]

dp[0][1]表示第0天结束时，手上没股票，说明第0天白天没有买股票，利润为0

故初始化为，

dp[0][0]=-prices[0]; dp[0][1]=0;

填表顺序

根据状态转移方程我们知道，想要推导出第i天的状态，我们需要利用第i-1天的状态。

所以填表顺序为，从左往右

返回值

根据状态表示，

dp[i][j]（j=0或1，0表示手上有股票，1表示手上没股票）

dp[i][j]表示第i天结束的时候拥有j状态时所能获得的最大利润。

我们需要返回最后一天的利润最大值。

故返回值为，

return fmax(dp[n-1][0],dp[n-1][1]);

代码实现

int maxProfit(int* prices, int pricesSize, int fee) {

    //0：手上有股票  1:手上没股票
    int n=pricesSize;
    int dp[n][2];

    dp[0][0]=-prices[0];
    dp[0][1]=0;
    for(int i=1;i<n;i++){
        dp[i][0]=fmax(dp[i-1][0],dp[i-1][1]-prices[i]);
        dp[i][1]=fmax(dp[i-1][0]+prices[i]-fee,dp[i-1][1]);

    }

    return fmax(dp[n-1][0],dp[n-1][1]);
}

123. 买卖股票的最佳时机 III

题目解析

状态表示

状态表示是根据经验＋题意得到的。

经验一般是以某个位置为结尾或者以某个位置为开始。

我们最开始可以想到的定义是，定义dp[i]表示从第0天开始到第i天所能获得的最大利润，但我们分析可以知道，该状态还可以继续细分，而且如果仅依靠这个状态没办法推导出状态转移方程，所以我们继续将状态进行细分。

根据手上有没有股票我们可以分为，第i天结束的时候，手上有股票，或者手上没有股票。

根据完成交易的次数我们可以分为，第i天结束的时候，完成交易次数是...。

如果将这些情况都考虑到，我们可以定义两个数组。

f[i][j]、g[i][j] (j=0或者1)

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

状态转移方程

我们想一想第i天的状态能不能由其他天的状态推导得到？

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

f[i-1][j]表示第i-1天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i-1][j]表示第i-1天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

针对f[i][j]，第i天结束时手上有股票，那么第i-1天结束时，要么手上有股票，然后第i天白天没有卖出股票，什么也没做，要么第i-1天结束时，手上没有股票，然后第i天白天买了股票。

如果第i-1天结束时，手上有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上有股票时的最大利润。如果i-1天结束时，手上没有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润减去第i天的股票价格，因为第i天白天我们买了股票。

针对g[i][j]，第i天结束时手上没有股票，那么第i-1天结束时，要么手上有股票，然后第i天白天卖出股票，要么第i-1天结束时，手上没有股票，然后第i天什么也没做。

如果第i-1天结束时，手上有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润加上第i天的股票价格。如果i-1天结束时，手上没有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润。

我们的交易次数的变化可以安排在卖出股票时，也就是当我们卖出股票，交易次数就增加一次。

所以我们的状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

初始化

根据状态转移方程，我们推导出第i天的状态，需要用到i-1天的状态值，所以我们需要初始化第零天的状态。注意， g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);中还需要访问前一天交易次数少一次的状态，这里也不能越界了。

我们先初始化第零天的状态。

f[0][0] f[0][1] f[0][2] g[0][0] g[0][1] g[0][2]

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

第零天不可能出现交易次数大于零的情况，所以对这些情况的初始化不能影响对后续状态的推导。

状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

为了不影响推导，这些值一定不能取到，所以我们初始化无穷小即可。

即，

f[0][1]=-INF; f[0][2]=-INF;

g[0][1]=-INF; g[0][2]=-INF;

f[0][0]表示第零天手上有股票，交易次数为零时所能获得的最大利润，也就是白天买了股票，所以f[0][0]=-prices[0]

g[0][0]表示第零天手上没有股票，交易次数为零时所能获得的最大利润，也就是白天什么都没有做，所以g[0][0]=0;

故状态转移方程为，

f[0][0]=-prices[0];

f[0][1]=-INF;

f[0][2]=-INF;

g[0][0]=0;

g[0][1]=-INF;

g[0][2]=-INF;

填表顺序

状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

由状态转移方程我们知道，需要推导出第i天的状态需要用到第i-1天的状态

所以填表顺序为从左往右

返回值

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

我们需要返回最后一天的最大利润，如果最后一天手上有股票，是不可能获得最大利润，因为必定有一个序列和前面的交易安排全部一样，唯一不一样的是最后一天没有买股票，那么它的最大利润一定比手上有股票时的最大利润大。所以我们只需要考虑手上没有股票时的最大利润即可。

所以返回值为

return fmax(g[n-1][0],fmax(g[n-1][1],g[n-1][2]));

代码实现

int maxProfit(int* prices, int pricesSize) {
    int n=pricesSize;
    int f[n][3];
    int g[n][3];
    //f:手上有股票
    //g:手上没有股票
    int INF=0x3f3f3f3f;
    f[0][0]=-prices[0];
    f[0][1]=-INF;
    f[0][2]=-INF;

    g[0][0]=0;
    g[0][1]=-INF;
    g[0][2]=-INF;
    for(int i=1;i<n;i++){
        f[i][0]=fmax(f[i-1][0],g[i-1][0]-prices[i]);
        f[i][1]=fmax(f[i-1][1],g[i-1][1]-prices[i]);
        f[i][2]=fmax(f[i-1][2],g[i-1][2]-prices[i]);

        g[i][0]=g[i-1][0];//为了防止j越界
        g[i][1]=fmax(f[i-1][0]+prices[i],g[i-1][1]);
        g[i][2]=fmax(f[i-1][1]+prices[i],g[i-1][2]);
    }

    return fmax(g[n-1][0],fmax(g[n-1][1],g[n-1][2]));
}

188. 买卖股票的最佳时机 IV

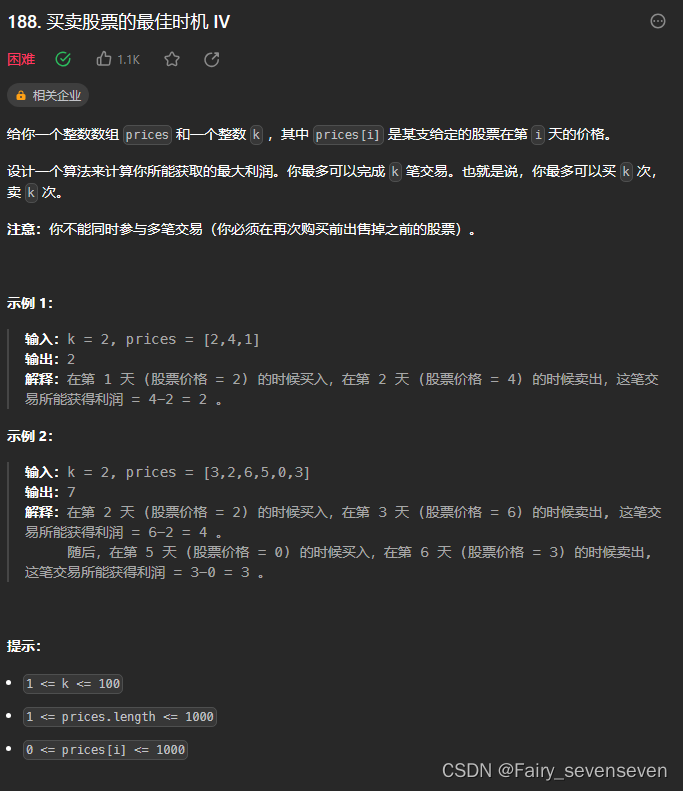
题目解析

状态表示

状态表示是根据经验＋题意得到的。

经验一般是以某个位置为结尾或者以某个位置为开始。

我们最开始可以想到的定义是，定义dp[i]表示从第0天开始到第i天所能获得的最大利润，但我们分析可以知道，该状态还可以继续细分，而且如果仅依靠这个状态没办法推导出状态转移方程，所以我们继续将状态进行细分。

根据手上有没有股票我们可以分为，第i天结束的时候，手上有股票，或者手上没有股票。

根据完成交易的次数我们可以分为，第i天结束的时候，完成交易次数是...。

如果将这些情况都考虑到，我们可以定义两个数组。

f[i][j]、g[i][j] (j=0、1、2...或者k)

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

状态转移方程

我们想一想第i天的状态能不能由其他天的状态推导得到？

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

f[i-1][j]表示第i-1天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i-1][j]表示第i-1天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

针对f[i][j]，第i天结束时手上有股票，那么第i-1天结束时，要么手上有股票，然后第i天白天没有卖出股票，什么也没做，要么第i-1天结束时，手上没有股票，然后第i天白天买了股票。

如果第i-1天结束时，手上有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上有股票时的最大利润。如果i-1天结束时，手上没有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润减去第i天的股票价格，因为第i天白天我们买了股票。

针对g[i][j]，第i天结束时手上没有股票，那么第i-1天结束时，要么手上有股票，然后第i天白天卖出股票，要么第i-1天结束时，手上没有股票，然后第i天什么也没做。

如果第i-1天结束时，手上有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润加上第i天的股票价格。如果i-1天结束时，手上没有股票，第i天结束时手上有股票的最大利润就等于i-1天结束时，手上没有股票时的最大利润。

我们的交易次数的变化可以安排在卖出股票时，也就是当我们卖出股票，交易次数就增加一次。

所以我们的状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

初始化

根据状态转移方程，我们推导出第i天的状态，需要用到i-1天的状态值，所以我们需要初始化第零天的状态。注意， g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);中还需要访问前一天交易次数少一次的状态，这里也不能越界了。

我们先初始化第零天的状态。

第零天不可能出现交易次数大于零的情况，所以对这些情况的初始化不能影响对后续状态的推导。

状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

为了不影响推导，这些值一定不能取到，所以我们初始化无穷小即可。

对于第零天交易次数为零的状态，有f[0][0]和g[0][0]

分别表示第零天结束时手上有股票，和手上没有股票的两种情况。

很容易得到，

f[0][0]=-prices[0]; g[0][0]=0;

故，我们可以先把所有状态初始化无穷小，然后把第零天交易次数为零的状态再初始化，即：

    for(int i=0;i<n;i++){
        memset(f[i],-0x3f,sizeof(f[i]));
        memset(g[i],-0x3f,sizeof(g[i]));
    }
    f[0][0]=-prices[0];
    g[0][0]=0;

填表顺序

状态转移方程为，

f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);

g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);

由状态转移方程我们知道，需要推导出第i天的状态需要用到第i-1天的状态

所以填表顺序为从左往右

返回值

f[i][j]表示第i天结束的时候，手上有股票，完成交易次数为j次，所能获得的最大利润。

g[i][j]表示第i天结束的时候，手上没有股票，完成交易次数为j次，所能获得的最大利润。

我们需要返回最后一天的最大利润，如果最后一天手上有股票，是不可能获得最大利润，因为必定有一个序列和前面的交易安排全部一样，唯一不一样的是最后一天没有买股票，那么它的最大利润一定比手上有股票时的最大利润大。所以我们只需要考虑手上没有股票时的最大利润即可。

即：

int ret=0;
    for(int i=0;i<=k;i++){
        ret=fmax(ret,g[n-1][i]);
    }
    return ret;

代码实现

int maxProfit(int k, int* prices, int pricesSize) {
    int n=pricesSize;
    int f[n][k+1];
    int g[n][k+1];
    //f表示手上有股票
    //g表示手上没有股票
    for(int i=0;i<n;i++){
        memset(f[i],-0x3f,sizeof(f[i]));
        memset(g[i],-0x3f,sizeof(g[i]));
    }
    f[0][0]=-prices[0];
    g[0][0]=0;

    for(int i=1;i<n;i++){
        for(int j=0;j<=k;j++){
            f[i][j]=fmax(f[i-1][j],g[i-1][j]-prices[i]);
            if(j==0) g[i][j]=g[i-1][j];//防止j越界
            else g[i][j]=fmax(f[i-1][j-1]+prices[i],g[i-1][j]);
        }
    }

    int ret=0;
    for(int i=0;i<=k;i++){
        ret=fmax(ret,g[n-1][i]);
    }
    return ret;
}

结尾

今天我们学习了动态规划的思想，动态规划思想和数学归纳法思想有一些类似，动态规划在模拟数学归纳法的过程，已知一个最简单的基础解，通过得到前项与后项的推导关系，由这个最简单的基础解，我们可以一步一步推导出我们希望得到的那个解，把我们得到的解依次存放在dp数组中，dp数组中对应的状态，就像是数列里面的每一项。最后感谢您阅读我的文章，对于动态规划系列，我会一直更新，如果您觉得内容有帮助，可以点赞加关注，以快速阅读最新文章。

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！