基于鸢尾花数据集的逻辑回归分类实践

重要知识点

逻辑回归 原理简介：

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：
$$logi(z)=\frac{1}{1+e^{-z}}$$

其对应的函数图像可以表示如下:

import numpy as np
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))

plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

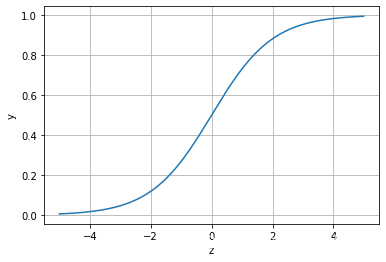
通过上图我们可以发现 Logistic 函数是单调递增函数，并且在z=0的时候取值为0.5，并且$logi(\cdot )$函数的取值范围为$(0,1)$。

而回归的基本方程为$z=w_0+{\sum }_i^N{w}_i{x}_i$，

将回归方程写入其中为：
$$p=p(y=1|x,\theta )=h_{\theta }(x,\theta )=\frac{1}{1+e^{-(w_0+{\sum }_i^N{w}_i{x}_i)}}$$

所以, $p(y=1|x,\theta )=h_{\theta }(x,\theta )$，$p(y=0|x,\theta )=1-h_{\theta }(x,\theta )$

逻辑回归从其原理上来说，逻辑回归其实是实现了一个决策边界：对于函数 $y=\frac{1}{1+e^{-z}}$,当 $z=>0$时,$y=>0.5$,分类为1，当 $z<0$时,$y<0.5$,分类为0，其对应的$y$值我们可以视为类别1的概率预测值.

对于模型的训练而言：实质上来说就是利用数据求解出对应的模型的特定的$w$。从而得到一个针对于当前数据的特征逻辑回归模型。

而对于多分类而言，将多个二分类的逻辑回归组合，即可实现多分类。

导入包

##  基础函数库
import numpy as np 
import pandas as pd

## 绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns

本次我们选择鸢花数据（iris）进行方法的尝试训练，该数据集一共包含5个变量，其中4个特征变量，1个目标分类变量。共有150个样本，目标变量为
花的类别 其都属于鸢尾属下的三个亚属，分别是山鸢尾
(Iris-setosa)，变色鸢尾(Iris-versicolor)和维吉尼亚鸢尾(Iris-virginica)。包含的三种鸢尾花的四个特征，分别是花萼长度(cm)、花萼宽度(cm)、花瓣长度(cm)、花瓣宽度(cm)，这些形态特征在过去被用来识别物种。

变量	描述
sepal length	花萼长度(cm)
sepal width	花萼宽度(cm)
petal length	花瓣长度(cm)
petal width	花瓣宽度(cm)
target	鸢尾的三个亚属类别,‘setosa’(0), ‘versicolor’(1), ‘virginica’(2)

导入数据

## 我们利用 sklearn 中自带的 iris 数据作为数据载入，并利用Pandas转化为DataFrame格式
from sklearn.datasets import load_iris
data = load_iris() #得到数据特征
iris_target = data.target #得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) #利用Pandas转化为DataFrame格式

查看信息

## 利用.info()查看数据的整体信息
iris_features.info()

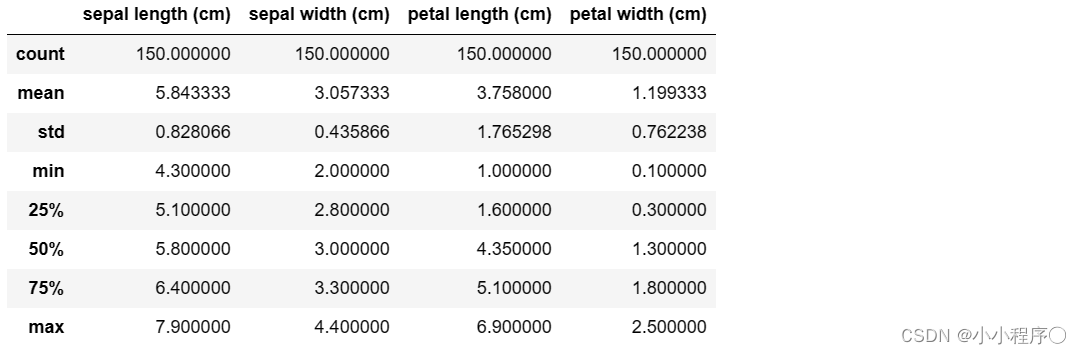
## 对于特征进行一些统计描述
iris_features.describe()

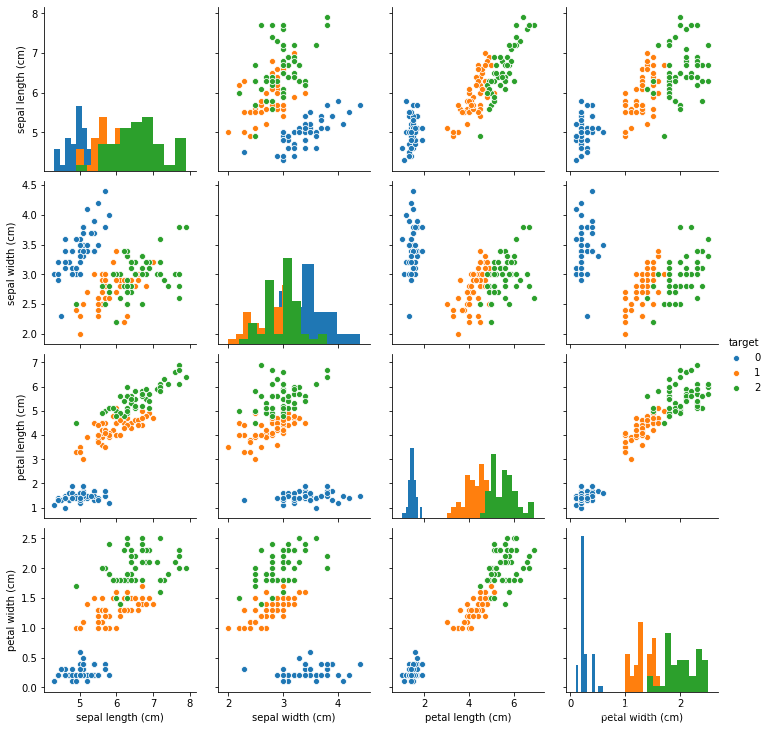
数据可视化

## 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝，防止对于原始数据的修改
iris_all['target'] = iris_target
## 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()

# 箱线图
for col in iris_features.columns:
    sns.boxplot(x='target', y=col, saturation=0.5,palette='pastel', data=iris_all)
    plt.title(col)
    plt.show()

训练和预测模型

## 为了正确评估模型性能，将数据划分为训练集和测试集，并在训练集上训练模型，在测试集上验证模型性能。
from sklearn.model_selection import train_test_split

## 选择其类别为0和1的样本 （不包括类别为2的样本）
iris_features_part = iris_features.iloc[:100]
iris_target_part = iris_target[:100]

## 测试集大小为20%， 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size = 0.2, random_state = 2020)
## 从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
## 定义 逻辑回归模型 
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型
clf.fit(x_train, y_train)



## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)

查看结果

## 利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))

## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)