贝叶斯球
定义几个术语,描述贝叶斯球在一个结点上的动作:
- 通过(pass through):从当前结点的父结点方向过来的球,可以访问当前结点的任意子结点(父->子)。从当前节点的子结点方向过来的球,可以访问当前结点的任意父结点。(子 -> 父)
- 反弹(bounce back):从当前结点的父结点方向过来的球,可以访问当前结点的任意父结点。(父->父)从当前节点的子结点方向过来的球,可以访问当前结点的任意子结点。(子 -> 子)
- 截止(block):当前结点阻止贝叶斯球继续运动
贝叶斯球算法(规则):假设在贝叶斯网络中有一个按一定规则运动的球。已知中间结点(或结点集合)Z,如果球不能由结点X出发到达结点Y(或者由Y到X),则称X和Y关于Z独立。
规则:
- 未知结点:总能使贝叶斯球通过,同时还可以反弹从其子结点方向来的球。(父 -> 子)|(子-> 父/子)
- 已知结点:反弹从其父结点方向过来的球,截止从其子结点方向过来的球。(父 -> 父)|(子->“截止”)
三种简单的结构,其中灰色球表示已知节点
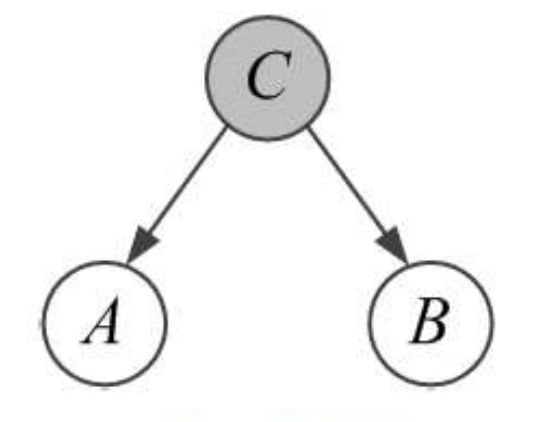
Tail to tail 模型:
A
⊥
B
∣
C
A\perp B|C
A⊥B∣C
P
(
A
,
B
∣
C
)
=
P
(
A
,
B
,
C
)
P
(
C
)
=
P
(
C
)
P
(
A
∣
C
)
P
(
B
∣
C
)
P
(
C
)
=
P
(
A
∣
C
)
P
(
B
∣
C
)
\begin{aligned} P(A,B|C)& =\frac{P(A,B,C)}{P(C)} \\ &=\frac{P(C)P(A|C)P(B|C)}{P(C)} \\ &=P(A|C)P(B|C) \end{aligned}
P(A,B∣C)=P(C)P(A,B,C)=P(C)P(C)P(A∣C)P(B∣C)=P(A∣C)P(B∣C)
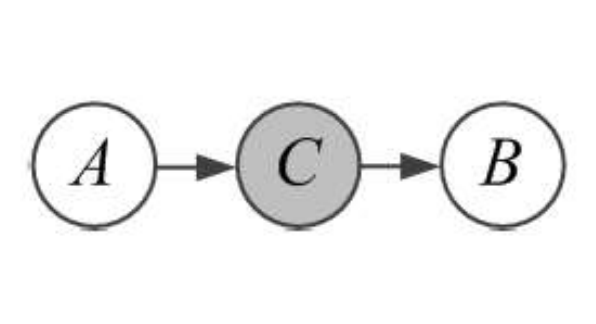
head to tail 模型:
A
⊥
B
∣
C
A\perp B|C
A⊥B∣C
P
(
A
,
B
∣
C
)
=
P
(
A
,
B
,
C
)
P
(
C
)
=
P
(
A
)
P
(
C
∣
A
)
P
(
B
∣
C
)
P
(
C
)
=
P
(
A
,
C
)
P
(
B
∣
C
)
P
(
C
)
=
P
(
A
∣
C
)
P
(
B
∣
C
)
\begin{aligned} P(A,B|C)& =\frac{P(A,B,C)}{P(C)} \\ &=\frac{P(A)P(C|A)P(B|C)}{P(C)} \\ &=\frac{P(A,C)P(B|C)}{P(C)}\\ &=P(A|C)P(B|C) \end{aligned}
P(A,B∣C)=P(C)P(A,B,C)=P(C)P(A)P(C∣A)P(B∣C)=P(C)P(A,C)P(B∣C)=P(A∣C)P(B∣C)
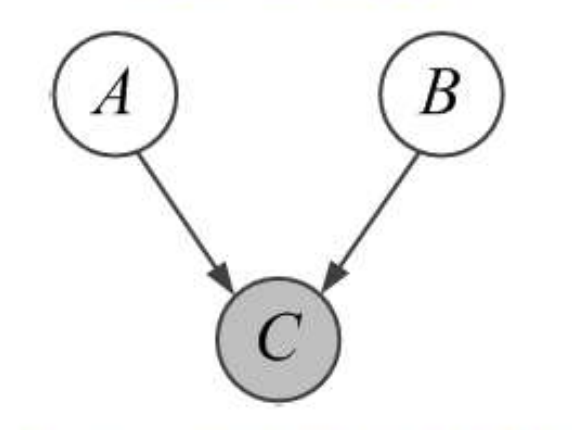
head to head 模型: A ⊥ B A\perp B A⊥B, A ⊥̸ B ∣ C A \not\perp B|C A⊥B∣C
例子:A 和 B 是否关于 F 条件独立?
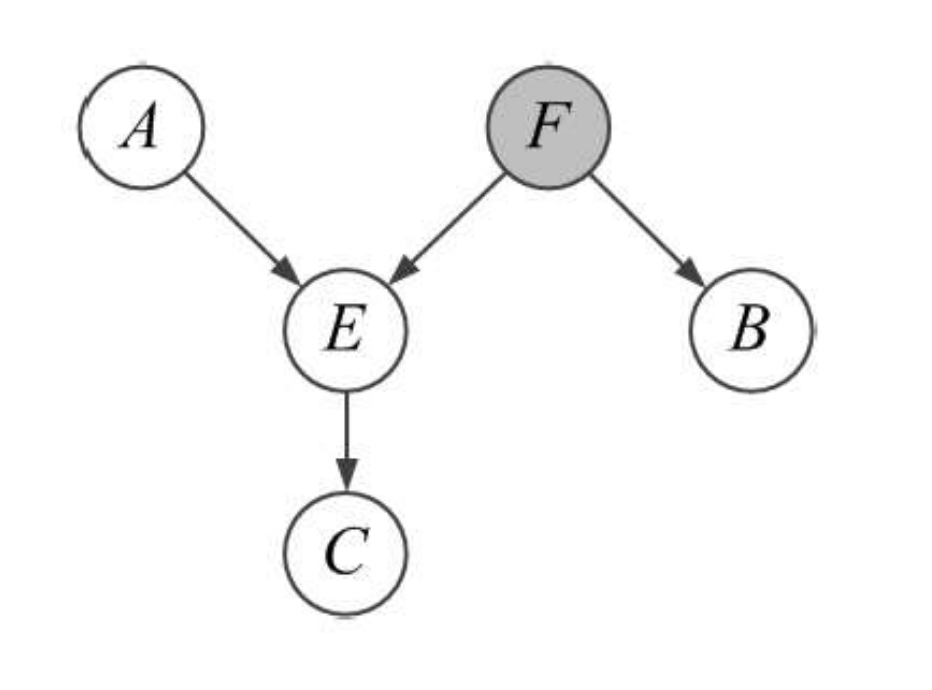
首先贝叶斯球从A出发滚到F处,F为已知节点,反弹来自父节点的球,无法达到B,所以 A ⊥ B ∣ F A\perp B|F A⊥B∣F
例子:A 和 B 是否关于 C 条件独立?
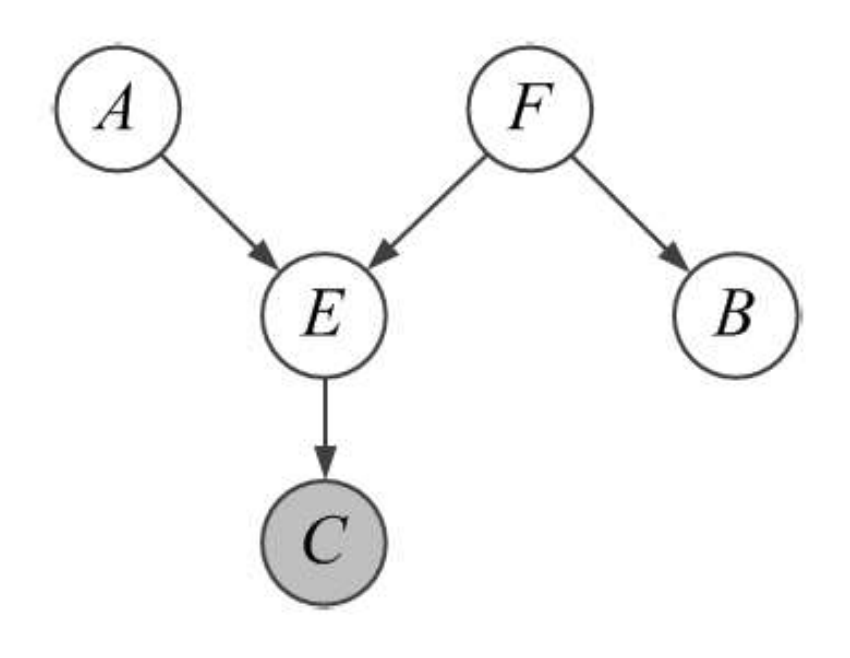
首先贝叶斯球从A出发可以直接滚到B处,所以 A ⊥̸ B ∣ C A\not\perp B|C A⊥B∣C










![[java] 注释](https://img-blog.csdnimg.cn/direct/ebe19bc21cff4b48b0eb0c5630347477.png)
![[论文阅读笔记28] 对比学习在多目标跟踪中的应用](https://img-blog.csdnimg.cn/direct/3a1ab023cdd74b8e904cea1382db8e64.png)