描述
插入排序是一种简单直观的排序算法。它的基本思想是将一个待排序的数据序列分为已排序和未排序两部分,每次从未排序序列中取出一个元素,然后将它插入到已排序序列的适当位置,直到所有元素都插入完毕,即完成排序。
实现思路
- 从第一个元素开始,将其视为已排序序列。
- 取出未排序序列的第一个元素,并将它与已排序序列的元素逐个比较。
- 如果找到一个已排序序列的元素大于待插入元素,将该元素后移一位。
- 重复步骤3,直到找到一个已排序序列的元素小于或等于待插入元素。
- 将待插入元素插入到这个位置。
- 重复步骤2-5,直到未排序序列中的所有元素都被插入到已排序序列中。
图解
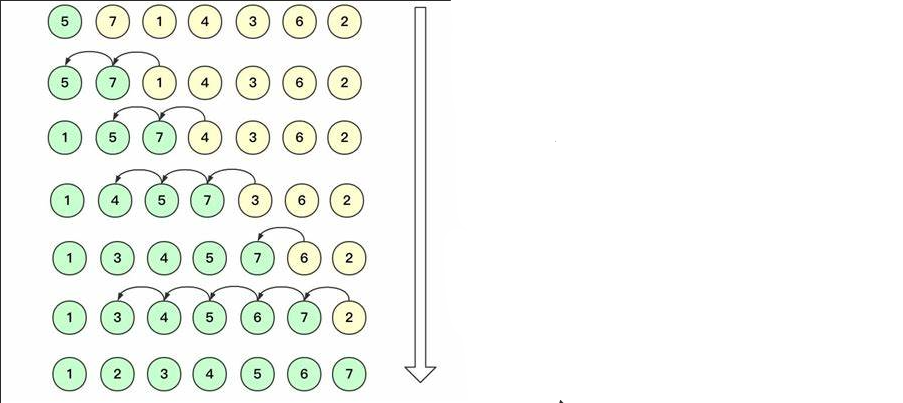
代码
#include <iostream>
#include <vector>
using namespace std;
void insertionSort(vector<int>& arr) {
int n = arr.size();
for (int i = 1; i < n; ++i) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
int main() {
vector<int> arr = {9, 5, 7, 1, 3};
insertionSort(arr);
cout << "插入排序 :" << endl;
for (int num : arr) {
cout << num << " ";
}
cout << endl;
return 0;
}
输出结果:

时间复杂度
根据循环次数,插入排序的平均时间复杂度为O(n2),最好情况下为O(n),最坏情况下为O(n2)。
空间复杂度
插入排序的空间复杂度为O(1)。
技巧
- 在内层循环中,可以通过将待插入元素与已排序序列的最后一个元素进行比较,而不是逐个比较已排序序列的元素,以提高效率。
- 可以使用二分查找来在已排序序列中找到待插入元素的插入位置,以进一步提高效率。
结论
坚持自己的梦想,即使没有翅膀也能飞翔。



![[java] 注释](https://img-blog.csdnimg.cn/direct/ebe19bc21cff4b48b0eb0c5630347477.png)
![[论文阅读笔记28] 对比学习在多目标跟踪中的应用](https://img-blog.csdnimg.cn/direct/3a1ab023cdd74b8e904cea1382db8e64.png)