那些最好的程序员不是为了得到更高的薪水或者得到公众的仰慕而编程，他们只是觉得这是一件有趣的事情！

---

---

📆Date: 2023年12月24日
🎬Author: 小 y 同 学
🔖Language: Python、C#、Matlab、C/C++

---

  将浮点数表示的度分秒1.40000进行无损精度的提取为1°40′00.0″，而不是1°39′99.9″。

🍀前言

  这是在《测量程序设计》这门课程所学习到的内容，在此十分地感谢老师分享的干货🌹

  在测量的角度表示方法中，为了记录和输入数据方便，通常会用类似ddd.mmsss的形式来表示角度ddd度mm分ss.s秒，例如将13度14分52.0秒表示为13.14520，那么如何在编程中正确的无精度的提取相应的度分秒成为了后续计算的首要且重要的问题，如果此步有误差，那么后续算法再精确、正确，也无法弥补。

  本文将以1.40000和13.14520的提取为例，从传统的提取方法、Python字符串截取提取的方法以及无损精度的提取方法这三种方法进行比较介绍。对于前两种方法提供Python源码，对于无损精度提取方法提供Python、C#、Matlab、C/C++源码。

🌸传统的提取方法

  这是网页上、以及一些书籍介绍的方法，之前一直没有发现问题，直到亲眼看到老师调试**1.40000被提取成1°39′99.9″**时，恍然大悟，实际运用中会有很大的问题！

🔖算法介绍

  通过直接对原始数据进行取整移动小数点的操作从而实现功能，流程描述如下：

1. 对13.14520进行取整，这样便得到了度13。
2. 将13.14520减去度的部分，同时乘100使得小数点右移两位变成14.520，再次进行取整，得到分14。
3. 将14.520减去分的部分，得到秒52.0；提取结束。

---

🧾Python源码

def DMSToDMSError(dmsAngle: float) -> list:
    d = int(dmsAngle)
    m = int((dmsAngle - d) * 100)
    s = (dmsAngle - d - m / 100) * 10000
    return [d, m, s]


if __name__ == '__main__':
    a = 1.40000
    print(DMSToDMSError(float(a)))
    b = 13.14520
    print(DMSToDMSError(float(b)))  

运行效果：

  可以看出提取出现了误差，需要注意的是：Python中整数与整数运算是可以得到小数结果的，可以使用//进行整除，也可以使用int函数进行一个转换。

---

📌小结

  这种提取方式在一般测试数据时可能不会出现问题，但是对于1.40000会被提取成1°39′99.9″，在秒位上多出了约40秒(外业测量员两行泪😭)。

  这是由于计算机内部存储采用二进制来存储，对于浮点数会有精度损失问题，这也是编程中不能直接对浮点数用==来对浮点数进行直接比较的原因。

🌿Python字符串截取提取

🔖算法介绍

  这是笔者初学Python惯用的方法(太方便啦🤩)，流程描述如下：

1. 将浮点数13.14520使用格式化转为字符类型"13.1452000000"。
2. 将字符串调用.split()方法按照"."进行分割，变为列表[“13”,“14520”]。
3. 列表的0号元素即为度，用int函数转换即可。
4. 列表的1号元素前两个字符组合是分，字符串截取int转换即可。
5. 列表的1号元素余下字符组合是秒，需要注意的是秒是浮点类型，此处将余下部分"520"前两位"52"+“.”+余下部分"520"的剩余的字符"0"组成新字符"52.0"，使用float函数转换即可；提取结束。

---

🧾Python源码

def DMSToDMS2(dmsAngle: float) -> list:
    dmsAngleStr = f"{dmsAngle:.10f}"
    (D, MS) = dmsAngleStr.split('.')  # 以小数点为分隔符,第一个为D,第二个为MS
    M = MS[0:2]  # MS的前两个字符是M
    S1 = MS[2:4]  # MS的其余字符是S,其中前两位是整数部分
    S2 = MS[4:]  # MS的其余字符是S,余下是小数部分
    return [int(D), int(M), float(S1 + '.' + S2)]


if __name__ == '__main__':
    a = 1.40000
    print(DMSToDMS2(a))
    b = 13.14520
    print(DMSToDMS2(b))

运行效果：

---

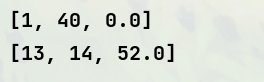
📌小结

  这种提取方法目前笔者还没遇到问题，对1.40000也可以做到无损精度提取，但是针对一些其他编程语言，难以或没有对字符串截取的操作、数据类型间的转换，将无法满足需求，算法对编程语言的通用性较差！

🍀无损精度的提取方法

🔖算法介绍

  与传统方法类似，但是不直接对原始数据进行操作，而是先将原始数据乘10000得到14000.0，再对整数部分提取即可避免1.39999…的问题。流程描述如下：

1. 将原始数据13.14520乘10000得到131452.0。
2. 将131452.0取整得到整数部分131452。
3. 对131452除以10000随后取整得到度13。
4. 将131452减去度的部分得到1452，除以100随后取整，得到分14。
5. 将131452.0减去度的部分、分的部分，得到秒52.0；提取结束。

---

🧾Python源码

def DMSToDMS(dmsAngle: float) -> list:
    dmsAngle *= 10000
    sAngle = int(dmsAngle)
    d = int(sAngle / 10000)
    m = int((sAngle - d * 10000) / 100)
    s = dmsAngle - d * 10000 - m * 100
    return [d, m, s]


if __name__ == '__main__':
    a = 1.40000
    print(DMSToDMS(float(a)))
    b = 13.14520
    print(DMSToDMS(float(b)))

运行效果：

---

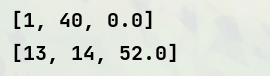
📜C#源码

using System.Net;

namespace DMSToDMS
{
    internal class Program
    {
        static (int d, int m, double s) DMSToDMS(double dmsAngle)
        {
            dmsAngle = dmsAngle * 10000;
            int sAngle = (int)dmsAngle;
            int d = sAngle / 10000;
            int m = (sAngle - d * 10000) / 100;
            double s = dmsAngle - d * 10000 - m * 100;
            return (d, m, s);
        }
        static void Main(string[] args)
        {
            double a = 1.40000;
            double b = 13.14520;
            double c = 13.14521;
            Console.WriteLine(DMSToDMS(a));
            Console.WriteLine(DMSToDMS(b));
            Console.WriteLine(DMSToDMS(c));
        }
    }
}

运行效果：

---

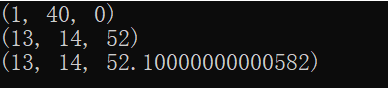
📃Matlab源码

% 无损精度提取度分秒函数
function dms = DMSToDMS(dmsAngle)
    dmsAngle = dmsAngle * 10000;
    sAngle = fix(dmsAngle);
    d = fix(sAngle/10000);
    m = fix((sAngle - d * 10000)/100);
    s = dmsAngle - d * 10000 - m * 100;
    dms = [d, m, s];
end

% 调用无损精度提取度分秒函数
dms=DMSToDMS(1.40000)
dms=DMSToDMS(13.14520)
dms=DMSToDMS(13.14521)

运行效果：

---

📑C/C++源码

#include<iostream>
using namespace std;

typedef struct 
{
	int d,m;
	double s;
}DMSAngle;

void DMSToDMS(double dmsAngle, DMSAngle* dms)
{
    dmsAngle = dmsAngle * 10000;
    int sAngle = (int)dmsAngle;
    dms->d = sAngle / 10000;
    dms->m = (sAngle - dms->d * 10000) / 100;
    dms->s = dmsAngle - dms->d * 10000 - dms->m * 100;
}

int main() {
    double a = 1.40000,b= 13.14520, c=13.14521;
    DMSAngle dmsAngle_a;
    DMSToDMS(a, &dmsAngle_a);

    DMSAngle dmsAngle_b;
    DMSToDMS(b, &dmsAngle_b);

    DMSAngle dmsAngle_c;
    DMSToDMS(c, &dmsAngle_c);

    cout<<dmsAngle_a.d<<" "<<dmsAngle_a.m<<" "<<dmsAngle_a.s<<endl;
    cout<<dmsAngle_b.d<<" "<<dmsAngle_b.m<<" "<<dmsAngle_b.s<<endl;
    cout<<dmsAngle_c.d<<" "<<dmsAngle_c.m<<" "<<dmsAngle_c.s<<endl;
    return 0;
}

运行效果：

---

📌小结

  此方法比较巧妙，区别绝大部分网页、包括一些书籍资料中的传统的错误方法，可做到无损精度提取，且不受编程语言限制，值得推荐！

🌹 结语

1. 值得注意的是：在Python3、Matlab等适合科学计算的编程语言中，整数与整数相运算的结果仍然为小数(与想象中的一致)；但是在C#、C/C++包括Python2这类编程语言中，整数与整数相运算的结果将会被截断取整，例如3/2将会得到1，而不是1.5，可以采用3/2.0的方式来避免；这也是编程中常常会遇到的小bug。
2. 由此也可以引发思考🤔或许有些算法我们在设计的适合毫无问题，而在实现的时候因为这些小细节而出现误差呢？
3. 含注释的源码已托管于Github仓库，关注下方公众号回复关键字"231224"获取~
4. 再次感谢授课老师给予的干货🌹🌹🌹

---

📧Summary

  有兴趣一起学习编程的小伙伴可以私聊小y一起学习,小y在Python,c/c++,C#和matlab语言上均有一定的基础😜😜😜

---

• 路虽远，行则将至；事虽难，做则必成。希望认真学习的你能够有所收获~
• 如果本文有幸可以帮到您，欢迎您的点赞、收藏与关注；您的点赞、收藏与关注是我创作的最大动力~

---