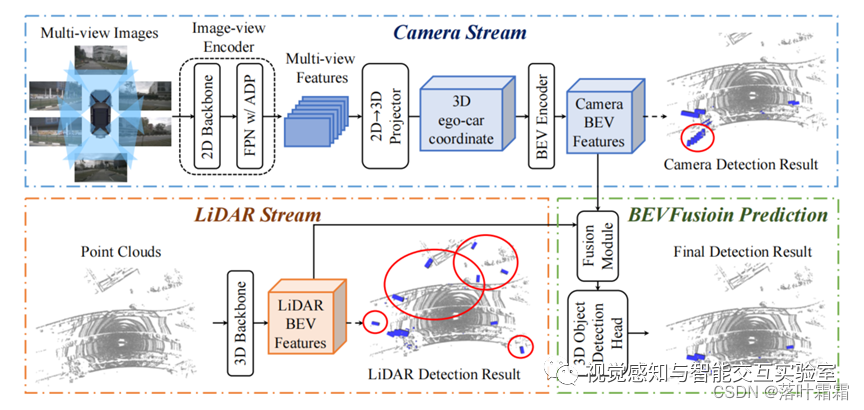
等腰三角形定义: 是指至少有两边相等的三角形。相等的两个边称为这个三角形的腰
二.证明
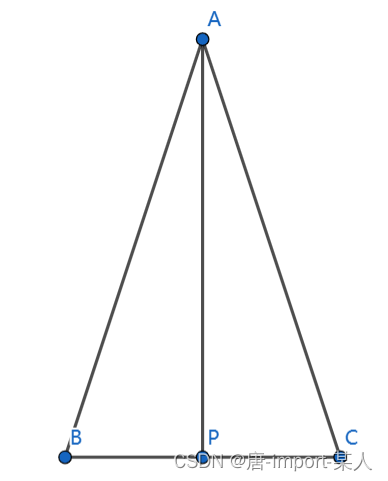
有等腰△ABC,AB和AC是腰,p是BC的中点
证明等腰三角形两底角相等 即
∠
A
B
P
=
∠
P
C
A
∠ABP=∠PCA
∠ABP=∠PCA
∴
∴
∴ 三角形内角和为180
∵
{
∠
A
B
P
+
∠
A
P
B
+
∠
B
A
P
=
180
°
∠
A
C
P
+
∠
A
P
C
+
∠
C
A
P
=
180
°
∠
A
B
C
+
∠
A
C
B
+
∠
B
A
C
=
180
°
∵\begin{cases} ∠ABP+∠APB+∠BAP=180° \\∠ACP+∠APC+∠CAP=180° \\∠ABC+∠ACB+∠BAC=180° \end{cases}
∵⎩
⎨
⎧∠ABP+∠APB+∠BAP=180°∠ACP+∠APC+∠CAP=180°∠ABC+∠ACB+∠BAC=180°
∴
A
B
=
A
C
,
p
为
B
C
中点
∴AB=AC,p为BC中点
∴AB=AC,p为BC中点
∵
∠
B
A
P
=
∠
C
A
P
=
∠
①
,
∠
B
A
C
=
2
∠
①
,
A
P
⊥
B
C
∵∠BAP=∠CAP=∠①,∠BAC=2∠①,AP⊥BC
∵∠BAP=∠CAP=∠①,∠BAC=2∠①,AP⊥BC
∵
{
∠
A
B
P
+
∠
A
P
B
+
∠
①
=
180
°
∠
A
C
P
+
∠
A
P
C
+
∠
①
=
180
°
∠
A
B
C
+
∠
A
C
B
+
2
∠
①
=
180
°
∵\begin{cases} ∠ABP+∠APB+∠①=180° \\∠ACP+∠APC+∠①=180° \\∠ABC+∠ACB+2∠①=180° \end{cases}
∵⎩
⎨
⎧∠ABP+∠APB+∠①=180°∠ACP+∠APC+∠①=180°∠ABC+∠ACB+2∠①=180°
∴
A
P
⊥
B
C
∴AP⊥BC
∴AP⊥BC
∵
∠
A
P
C
=
∠
A
P
B
=
90
°
∵∠APC=∠APB=90°
∵∠APC=∠APB=90°
∵
{
∠
A
B
P
+
∠
①
+
90
°
=
180
°
∠
P
C
A
+
∠
①
+
90
°
=
180
°
∵\begin{cases} ∠ABP+∠①+90°=180° \\∠PCA+∠①+90°=180° \end{cases}
∵{∠ABP+∠①+90°=180°∠PCA+∠①+90°=180°
∵
∠
A
B
P
=
∠
P
C
A
∵∠ABP=∠PCA
∵∠ABP=∠PCA

![[动态规划]完全背包问题及其优化](https://img-blog.csdnimg.cn/img_convert/72423ab416f11cad6c40e4f396406aa8.jpeg)