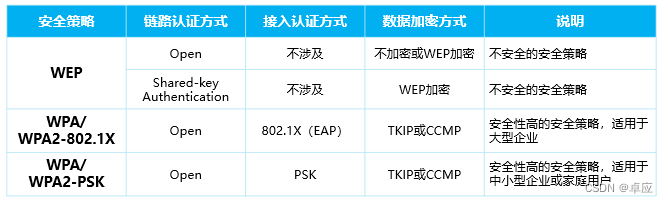
GitHub - LittleFox99/B_A_star: Bidirectional A Star

其中a，b分别为双向A*搜索的权重 

#-*- coding:utf-8 -*-
# @Time    : 2020/11/11 1:21 下午
# @Author  : LittleFox99
# File : a_star.py
# 参考：
# https://blog.csdn.net/lustyoung/article/details/105027607
# https://www.jianshu.com/p/5704e67f40aa
import numpy as np
import queue
from queue import PriorityQueue
from pylab import *
import matplotlib.pyplot as plt


class A_star:
    def __init__(self, a, b, start, end, max_row, max_col, barrier_map):
        """
        A_star 初始化
        :param a:
        :param b:
        :param start:
        :param end:
        :param max_row:
        :param max_col:
        :param barrier_map:
        """

        # 权重参数
        self.a = a
        self.b = b
        # 起始点、终点
        self.start = start
        self.end = end
        # 相遇点
        self.stop_point = None
        self.stop_point_back = None
        #采用优先队列实现的小顶堆，用于存放待扩展结点，同时利用f值作为排序指标；
        self.opened_list1 = PriorityQueue()
        self.opened_list2 = PriorityQueue()
        self.open_all_list = []
        #储存记录所有走过的openlist
        self.open_list = set()
        #采用set（红黑树）实现，便于快速查找当前point是否存在于closed_list中；
        self.closed_list1 = set()
        self.closed_list2 = set()
        # 地图边界
        self.max_row = max_row
        self.max_col = max_col
        # 论文中设定为四个移动方向
        self.direction = [[0, 1], [0, -1], [1, 0], [-1, 0]]
        # 障碍地图
        self.barrier_map = barrier_map
        #遍历结点数
        self.travel_num = 0



    def bound(self, row, col):
        """
        边界条件检测：
        1.如果该点坐标超出地图区域，则非法
        2.如果该点是障碍，则非法
        :param row:
        :param col:
        :return:
        """
        if row < 0 or row > self.max_row:
            return True
        if col < 0 or col > self.max_col:
            return True
        if [row, col] in self.barrier_map:
            return True
        return False

    def euclidean_distance(self, point1, point2):
        """
        欧式距离计算
        :param point1:
        :param point2:
        :return:
        """
        x_ = abs(point1.getx() - point2.getx())
        y_ = abs(point1.gety() - point2.gety())
        return ((x_**2)+(y_**2))**(0.5)*1.0


    def find_path(self, point):
        """
        用栈回溯查找B-A*给出的路径
        :param point:
        :return:
        """
        stack = []
        father_point = point
        while father_point is not None:
            stack.append(father_point.get_coordinate())
            father_point = father_point.father
        return stack

    def heuristic_h(self, end_point, point1, point2):
        """
        启发函数h值计算
        h：正向搜索当前点n1到终点的欧式距离
        h_：正向搜索当前点n1到反向搜索当前点n2的距离
        :param end_point:
        :param point1:
        :param point2:
        :return:
        """
        h = self.euclidean_distance(point1, end_point)
        h_ = self.euclidean_distance(point1, point2)
        return (1 - self.b) * (h*1.0 / (1 + self.a) + self.a * h_*1.0 / (1 + self.a))

    def heuristic_g(self, point):
        """
        启发函数g值计算
        g:当前点父亲的g值
        g_:当前点到其父亲的欧式距离
        :param point:
        :return:
        """
        g = point.father.g
        g_ = self.euclidean_distance(point, point.father)
        return self.b * (g + g_)*1.0

    def heuristic_f(self, h, g):
        # 计算启发式函数f值
        return h + g


    def compute_child_node(self, current_point, back_current_point, search_forward):
        """
        遍历当前点的子节点
        :param current_point: 当前点
        :param back_current_point: 相反方向搜索的当前点
        :param search_forward: 搜索方向设置，True为正向，反之亦然
        :return:
        """
        # 四个方向的遍历
        for direct in self.direction:
            col_index = current_point.gety() + direct[0]
            row_index = current_point.getx() + direct[1]
            # 创建子节点，将当前点设置为子节点的父节点
            child_point = Point(row_index, col_index, current_point)
            # 查找open_list中是否存在子节点中，用于备份节点
            old_child_point = None
            #前向搜索
            if search_forward == True:

                #计算子节点各个启发函数值
                child_point.h = self.heuristic_h(self.end, current_point, back_current_point)
                child_point.g = self.heuristic_g(child_point)
                child_point.f = self.heuristic_f(child_point.h, child_point.g)

                # 边界检测, 如果它不可通过或者已经在关闭列表中, 跳过
                if (row_index, col_index) in self.closed_list1 or self.bound(row_index, col_index)==True:
                    continue
                else:
                    self.travel_num = self.travel_num + 1
                    # 通过检测则将子节点加入openlist（记录所有加入过openlist的点）
                    self.open_list.add(child_point.get_coordinate())
                    # 找到最短路径
                    if (row_index, col_index) in self.closed_list2:
                        self.stop_point_back = self.search_back_point(child_point, self.open_all_list)

                        self.stop_point = child_point
                        if self.stop_point_back is None:
                            self.stop_point_back = self.stop_point
                        print("forward!")
                        return True
                    """
                    如果可到达的节点存在于OPEN1列表中，称该节点为x点，计算经过n1点到达x点的g1(x)值，
                    如果该g1(x)值小于原g1(x)值，则将n1点作为x点的父节点，更新OPEN1列表中的f1(x)和g1(x)。
                    """
                    tmp_queue = [] # opened_list的备份
                    while not self.opened_list1.empty():
                        tmp_point = self.opened_list1.get()
                        if child_point.get_coordinate() == tmp_point.get_coordinate(): #找到x点，跳过
                            old_child_point = tmp_point
                            continue
                        tmp_queue.append(tmp_point)
                    while len(tmp_queue) != 0:
                        self.opened_list1.put(tmp_queue.pop())
                    if old_child_point is None: #如果没找到，直接加入子节点
                        self.opened_list1.put(child_point)
                    else:
                        # 找到x点
                        # 用g值为参考检查新的路径是否更好。更低的g值意味着更好的路径。
                        if old_child_point.g > child_point.g:
                            self.opened_list1.put(child_point)
                        else:
                            # print(2)
                            self.opened_list1.put(old_child_point)
                            # print(2)

            # 反向搜索，同理如上
            else:
                # 边界检测, 如果它不可通过或者已经在关闭列表中, 跳过
                child_point.h = self.heuristic_h(self.start, current_point, back_current_point)
                child_point.g = self.heuristic_g(child_point)
                child_point.f = self.heuristic_f(child_point.h, child_point.g)
                if (row_index, col_index) in self.closed_list2 or self.bound(row_index, col_index):
                    continue
                else:
                    self.travel_num = self.travel_num + 1
                    self.open_list.add(child_point.get_coordinate())
                    # 找到最短路径
                    if (row_index, col_index) in self.closed_list1:
                        # self.stop_point_back = self.search_father_point(child_point,self.opened_list2)
                        self.stop_point_back = self.search_back_point(child_point, self.open_all_list)

                        self.stop_point = child_point
                        if self.stop_point_back is None:
                            self.stop_point_back = self.stop_point
                        print("backward!")
                        return True
                    tmp_queue = []
                    while not self.opened_list2.empty():
                        tmp_point = self.opened_list2.get()
                        if child_point.get_coordinate() == tmp_point.get_coordinate():
                            old_child_point = tmp_point
                            continue
                        tmp_queue.append(tmp_point)
                    while len(tmp_queue) != 0:
                        self.opened_list2.put(tmp_queue.pop())
                    if old_child_point is None: #open_list没有找到子节点，则将
                        self.opened_list2.put(child_point)
                    else:
                        # 用g值为参考检查新的路径是否更好。更低的G值意味着更好的路径。
                        if old_child_point.g > child_point.g:
                            self.opened_list2.put(child_point)
                        else:
                            self.opened_list2.put(old_child_point)
                            # print(3)
        return False

    def search_back_point(self, point, opened_list):
        back_point = None
        while len(opened_list)!=0:
            tmp_point = opened_list.pop()
            if point.get_coordinate() == tmp_point.get_coordinate():
                return tmp_point
        return back_point




    def search(self):
        # 将起始点s设置为正向当前结点n1、终点e设置为反向当前结点n2
        current_point1 = self.start
        current_point2 = self.end
        # 并加入open1、open2
        self.opened_list1.put(current_point1)
        self.opened_list2.put(current_point2)
        forward_path, backward_path =None, None
        # opened_list1与opened_list2全部非空,输出寻路提示失败
        find_stop = False
        min_f_point1 = self.opened_list1.get()
        self.closed_list1.add((min_f_point1.getx(), min_f_point1.gety()))
        min_f_point2 = self.opened_list2.get()
        self.closed_list2.add((min_f_point2.getx(), min_f_point2.gety()))



        while True:
            # # 取出open_list1中f值最小的点，加入closed_list1
            # 将其作为当前结点，遍历寻找它的子节点
            # min_f_point1 = self.opened_list1.get()
            # self.closed_list1.add((min_f_point1.getx(), min_f_point1.gety()))
            self.open_all_list.append(current_point1)
            self.open_all_list.append(current_point2)
            find_stop = self.compute_child_node(current_point1, current_point2, True)
            if find_stop:
                # forward_path = self.find_path(current_point1)
                forward_path = self.find_path(self.stop_point)
                backward_path = self.find_path(self.stop_point_back)
                break
            # min_f_point1 = self.opened_list1.get()
            # print(1)
            min_f_point1 = self.opened_list1.get()
            # self.open_all_list.append(min_f_point1)
            self.closed_list1.add((min_f_point1.getx(), min_f_point1.gety()))
            current_point1 = min_f_point1
            self.open_all_list.append(current_point1)


            # 取出open_list1中f值最小的点，加入closed_list1
            # current_point1 = self.opened_list1.get()

            find_stop = self.compute_child_node(current_point2, current_point1, False)
            if find_stop:
                forward_path = self.find_path(self.stop_point)
                backward_path = self.find_path(self.stop_point_back)
                # backward_path = self.find_path(self.stop_point)

                break
            # min_f_point2 = self.opened_list2.get()
            min_f_point2 = self.opened_list2.get()
            # self.open_all_list.append(min_f_point1)
            self.closed_list2.add((min_f_point2.getx(), min_f_point2.gety()))
            current_point2 = min_f_point2
            if self.opened_list1.qsize() == 0 or self.opened_list2.qsize() == 0:
                break


            # current_point2 = self.opened_list2.get()
        if backward_path==None and forward_path==None:
            print("Fail to find the path!")
            return None
        else:
            forward_path = forward_path + backward_path
        return forward_path, self.open_list, self.stop_point, self.travel_num

class Point:
    """
    Point——地图上的格子，或者理解为点
    1.坐标
    2.g,h,f，father
    """
    def __init__(self, x, y, father):
        self.x = x
        self.y = y
        self.g = 0
        self.h = 0
        self.f = 0
        self.father = father

    # 用于优先队列中f值的排序
    def __lt__(self, other):
        return self.f < other.f

    # 获取x坐标
    def getx(self):
        return self.x

    # 获取y坐标
    def gety(self):
        return self.y

    # 获取x, y坐标
    def get_coordinate(self):
        return self.x, self.y


def draw_path(max_row, max_col, barrier_map, path=None, openlist=None, stop_point=None, start=None ,end=None):
    """
    画出B-A*算法的结果模拟地图
    :param max_row:地图x最大距离
    :param max_col:地图y最大距离
    :param barrier_map:障碍地图
    :param path:B-A*给出的较优路径
    :param openlist:B-A*中的openlist
    :param stop_point:B-A*中的相遇结点
    :param start:起始点
    :param end:终点
    :return:
    """
    """划分数组的x,y坐标"""
    barrier_map_x = [i[0] for i in barrier_map]
    barrier_map_y = [i[1] for i in barrier_map]
    path_x = [i[0] for i in path]
    path_y = [i[1] for i in path]
    open_list_x = [i[0] for i in openlist]
    open_list_y = [i[1] for i in openlist]
    """对画布进行属性设置"""

    # plt.subplot(2, 2, subplot)
    plt.figure(figsize=(15, 15))  # 为了防止x,y轴间隔不一样长，影响最后的表现效果，所以手动设定等长
    plt.xlim(-1, max_row)
    plt.ylim(-1, max_col)
    my_x_ticks = np.arange(0, max_row, 1)
    my_y_ticks = np.arange(0, max_col, 1)
    plt.xticks(my_x_ticks)  # 竖线的位置与间隔
    plt.yticks(my_y_ticks)
    plt.grid(True)  # 开启栅格
    """画图"""
    plt.scatter(barrier_map_x, barrier_map_y, s=500, c='k', marker='s')
    plt.scatter(open_list_x, open_list_y, s=500, c='cyan', marker='s')
    plt.scatter(path_x, path_y,s=500, c='r', marker='s')
    plt.scatter(stop_point.getx(), stop_point.gety(), s=500, c='g', marker='s')
    plt.scatter(start.getx(),start.gety(),s=500, c='b', marker='s')
    plt.scatter(end.getx(), end.gety(), s=500, c='b', marker='s')
    plt.title("Bidirectiional A Star , a = {}, b = {}".format(a, b))
    print(path)
    plt.savefig("result_pic/a_{},b_{}.png".format(a, b))
    plt.show()


def draw_arg(travel_num, path_num, a_list, b_list):
    markes = ['-o', '-s', '-^', '-p', '-^','-v']

    travel_num = np.array(travel_num)
    path_num = np.array(path_num)
    fig,ax = plt.subplots(2, 1, figsize=(15,12))
    for i in range(0, 6):
        ax[0].plot(a_list, travel_num[i*6:(i+1)*6], markes[i],label=b_list[i])
        ax[0].set_ylabel('Travel num')
        ax[1].plot(a_list, path_num[i*6:(i+1)*6], markes[i],label=b_list[i])
        ax[1].set_xlabel('The values of a')
        ax[1].set_ylabel('Path nun')
    ax[0].set_title('the two args of B-A*')
    box = ax[1].get_position()
    ax[1].set_position([box.x0, box.y0, box.width, box.height])
    ax[1].legend(loc='right', bbox_to_anchor=(1.1, 0.6), ncol=1, title="b")
    plt.savefig("ab.png")
    plt.show()


if __name__ == '__main__':

    """权重的值"""
    a_list = [2, 3, 4, 5, 6, 7]
    b_list = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6]
    """地图、障碍物的位置、起始点、终点"""
    max_row = 30
    max_col = 30
    # barrier_map = [[1, 2], [3, 5], [4,7],[6, 6], [11, 19], [11, 6],[11, 5],[12,5],[12,6],[11, 16], [11, 17], [11, 18], [7, 7]]
    barrier_map = [[6, 29], [7, 29], [8, 29], [6, 28], [7, 28], [8, 28], [6, 27], [7, 27], [8, 27], [6, 26], [7, 26],
                   [8, 26], [6, 25], [7, 25], [8, 25], [6, 24], [7, 24], [8, 24], [29, 25], [28, 25], [27, 25],
                   [26, 25], [25, 25], [24, 25], [23, 25], [22, 25], [21, 25], [29, 24], [28, 24], [27, 24], [26, 24],
                   [24, 24], [25, 24],
                   [23, 24], [22, 24], [21, 24], [20, 10], [21, 10], [22, 10], [23, 10], [24, 10], [20, 9], [21, 9],
                   [22, 9], [23, 9], [24, 9], [20, 8], [21, 8], [22, 8], [23, 8], [24, 8], [20, 7], [21, 7], [22, 7],
                   [23, 7], [24, 7], [20, 6], [21, 6], [22, 6], [23, 6], [24, 6], [20, 5], [21, 5], [22, 5], [23, 5],
                   [24, 5], [20, 4], [21, 4], [22, 4], [23, 4], [24, 4], [20, 3], [21, 3], [22, 3], [23, 3], [24, 3],
                   [20, 2], [21, 2], [22, 2], [23, 2], [24, 2], [20, 1], [21, 1], [22, 1], [23, 1], [24, 1], [20, 0],
                   [21, 0], [22, 0], [23, 0], [24, 0],
                   [16, 16], [16, 17], [16, 18], [17, 16], [17, 17], [17, 18], [18, 16], [18, 17], [18, 18], [19, 16],
                   [19, 17], [19, 18], [20, 16], [20, 17], [20, 18], [21, 16], [21, 17], [21, 18], [22, 16], [22, 17],
                   [22, 18], [23, 16], [23, 17], [23, 18], [24, 16], [24, 17], [24, 18], [25, 16], [25, 17], [25, 18],
                   [26, 16], [26, 17], [26, 18], [27, 16], [27, 17], [27, 18], [28, 16], [28, 17], [28, 18], [29, 16],
                   [29, 17], [29, 18]]
    # barrier_map = np.array(barrier_map)
    # start = Point(4, 5, None)
    # end = Point(18, 8, None)
    start = Point(27, 2, None)
    end = Point(0, 29, None)
    travel_point_num = []
    path_point_num = []

    """遍历权重的值，使用B-A*算法"""
    # for a, b in zip(a_list, b_list):
    for b in b_list:
        for a in a_list:
            print(a,b)
            path, open_list, stop_point, tp_num = A_star(a, b, start, end, max_row, max_col,barrier_map).search()
            if path is not None:
                # 找到路径
                print("Find the path!")
                travel_point_num.append(tp_num)
                path_point_num.append(len(path))
                draw_path(max_row, max_col, barrier_map, path, open_list, stop_point, start, end)
            else:
                print("Fail to find the path!")

    print(travel_point_num)
    print(path_point_num)
    draw_arg(travel_point_num, path_point_num, a_list, b_list)