KMP算法是一种字符串匹配算法,可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。本文将引导您学习KMP算法,阅读大约需要30分钟。
1、字符串匹配问题
所谓字符串匹配,是这样一种问题:“字符串 P 是否为字符串 S 的子串?如果是,它出现在 S 的哪些位置?” 其中 S 称为主串;P 称为模式串。下面的图片展示了一个例子。
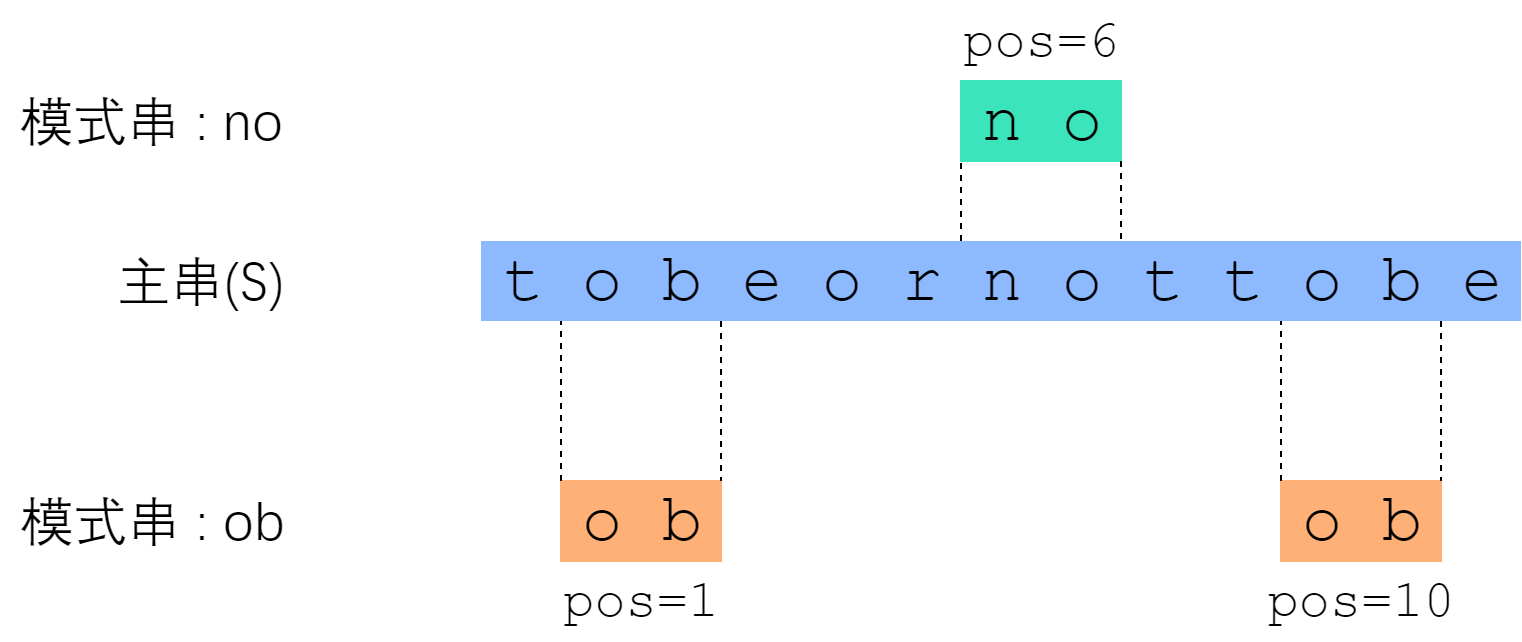
主串是那句著名的 “to be or not to be”,这里删去了空格。“no” 这个模式串的匹配结果是“出现了一次,从S[6]开始”;“ob”这个模式串的匹配结果是“出现了两次,分别从s[1]、s[10]开始”。按惯例,主串和模式串都以0开始编号。
字符串匹配是一个非常频繁的任务。例如,今有一份名单,你急切地想知道自己在不在名单上;又如,假设你拿到了一份文献,你希望快速地找到某个关键字所在的章节……凡此种种,不胜枚举。
我们先从最朴素的Brute-Force算法开始讲起。
2、Brute-Force
顾名思义,Brute-Force是一个纯暴力算法。说句题外话,我怀疑,“暴力”一词在算法领域表示“穷举、极低效率的实现”,可能就是源于这个英文词。
首先,我们应该如何实现两个字符串 A,B 的比较?所谓字符串比较,就是问“两个字符串是否相等”。最朴素的思想,就是从前往后逐字符比较,一旦遇到不相同的字符,就返回False;如果两个字符串都结束了,仍然没有出现不对应的字符,则返回True。实现如下:

既然我们可以知道“两个字符串是否相等”,那么最朴素的字符串匹配算法 Brute-Force 就呼之欲出了——
- 枚举 i = 0, 1, 2 ... , len(S)-len(P)
- 将 S[i : i+len(P)] 与 P 作比较。如果一致,则找到了一个匹配。
现在我们来模拟 Brute-Force 算法,对主串 “AAAAAABC” 和模式串 “AAAB” 做匹配:
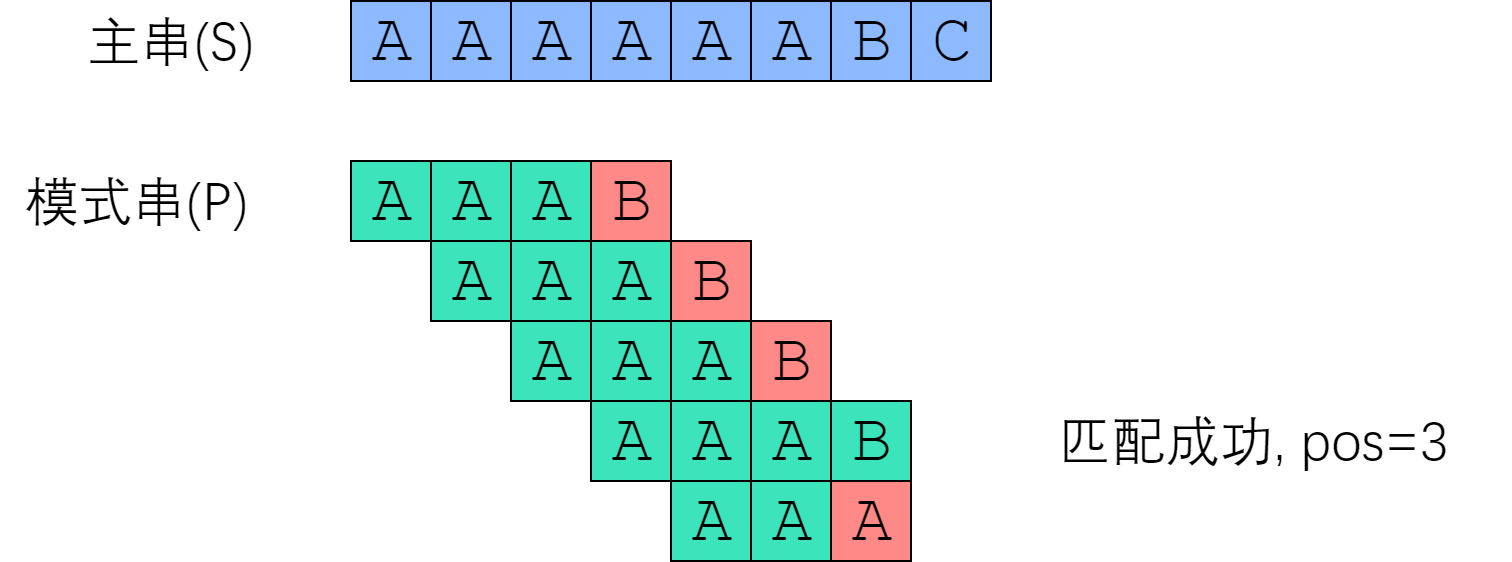
这是一个清晰明了的算法,实现也极其简单。下面给出Python和C++的实现:


我们成功实现了 Brute-Force 算法。现在,我们需要对它的时间复杂度做一点讨论。按照惯例,记 n = |S| 为串 S 的长度,m = |P| 为串 P 的长度。
考虑“字符串比较”这个小任务的复杂度。最坏情况发生在:两个字符串唯一的差别在最后一个字符。这种情况下,字符串比较必须走完整个字符串,才能给出结果,因此复杂度是 O(len) 的。
由此,不难想到 Brute-Force 算法所面对的最坏情况:主串形如“AAAAAAAAAAA...B”,而模式串形如“AAAAA...B”。每次字符串比较都需要付出 |P| 次字符比较的代价,总共需要比较 |S| - |P| + 1次,因此总时间复杂度是 O(|P|⋅(|S|−|P|+1))O(|P|\cdot (|S| - |P| + 1) ) . 考虑到主串一般比模式串长很多,故 Brute-Force 的复杂度是 O(|P|⋅|S|)O(|P| \cdot |S|) ,也就是 O(nm)的。这太慢了!
3、Brute-Force的改进思路
经过刚刚的分析,您已经看到,Brute-Force 慢得像爬一样。它最坏的情况如下图所示:

我们很难降低字符串比较的复杂度(因为比较两个字符串,真的只能逐个比较字符)。因此,我们考虑降低比较的趟数。如果比较的趟数能降到足够低,那么总的复杂度也将会下降很多。 要优化一个算法,首先要回答的问题是“我手上有什么信息?” 我们手上的信息是否足够、是否有效,决定了我们能把算法优化到何种程度。请记住:尽可能利用残余的信息,是KMP算法的思想所在。
在 Brute-Force 中,如果从 S[i] 开始的那一趟比较失败了,算法会直接开始尝试从 S[i+1] 开始比较。这种行为,属于典型的“没有从之前的错误中学到东西”。我们应当注意到,一次失败的匹配,会给我们提供宝贵的信息——如果 S[i : i+len(P)] 与 P 的匹配是在第 r 个位置失败的,那么从 S[i] 开始的 (r-1) 个连续字符,一定与 P 的前 (r-1) 个字符一模一样!

需要实现的任务是“字符串匹配”,而每一次失败都会给我们换来一些信息——能告诉我们,主串的某一个子串等于模式串的某一个前缀。但是这又有什么用呢?
4、跳过不可能成功的字符串比较
有些趟字符串比较是有可能会成功的;有些则毫无可能。我们刚刚提到过,优化 Brute-Force 的路线是“尽量减少比较的趟数”,而如果我们跳过那些绝不可能成功的字符串比较,则可以希望复杂度降低到能接受的范围。
那么,哪些字符串比较是不可能成功的?来看一个例子。已知信息如下:
- 模式串 P = "abcabd".
- 和主串从S[0]开始匹配时,在 P[5] 处失配。
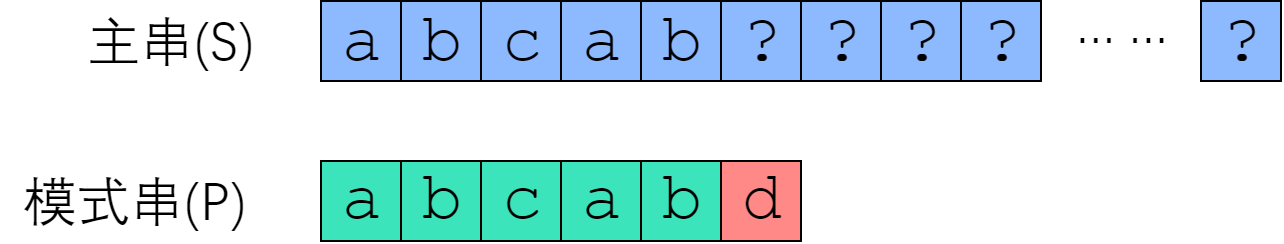
首先,利用上一节的结论。既然是在 P[5] 失配的,那么说明 S[0:5] 等于 P[0:5],即"abcab". 现在我们来考虑:从 S[1]、S[2]、S[3] 开始的匹配尝试,有没有可能成功?
从 S[1] 开始肯定没办法成功,因为 S[1] = P[1] = 'b',和 P[0] 并不相等。从 S[2] 开始也是没戏的,因为 S[2] = P[2] = 'c',并不等于P[0]. 但是从 S[3] 开始是有可能成功的——至少按照已知的信息,我们推不出矛盾。

带着“跳过不可能成功的尝试”的思想,我们来看next数组。
(1)next数组
next数组是对于模式串而言的。P 的 next 数组定义为:next[i] 表示 P[0] ~ P[i] 这一个子串,使得 前k个字符恰等于后k个字符 的最大的k. 特别地,k不能取i+1(因为这个子串一共才 i+1 个字符,自己肯定与自己相等,就没有意义了)。
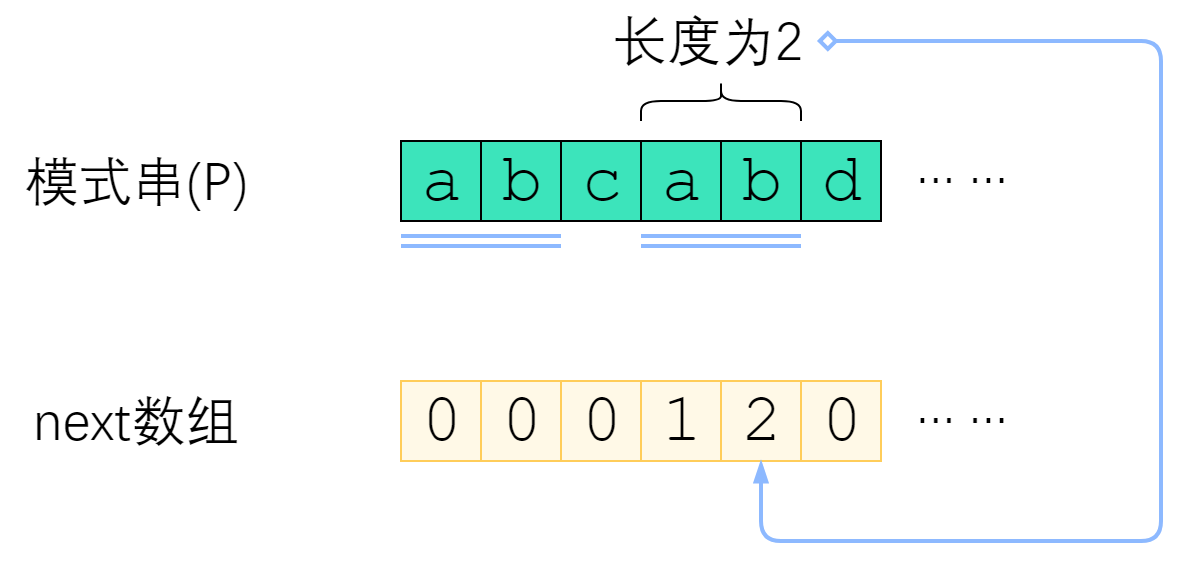
上图给出了一个例子。P="abcabd"时,next[4]=2,这是因为P[0] ~ P[4] 这个子串是"abcab",前两个字符与后两个字符相等,因此next[4]取2. 而next[5]=0,是因为"abcabd"找不到前缀与后缀相同,因此只能取0。
如果把模式串视为一把标尺,在主串上移动,那么 Brute-Force 就是每次失配之后只右移一位;改进算法则是每次失配之后,移很多位,跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢?
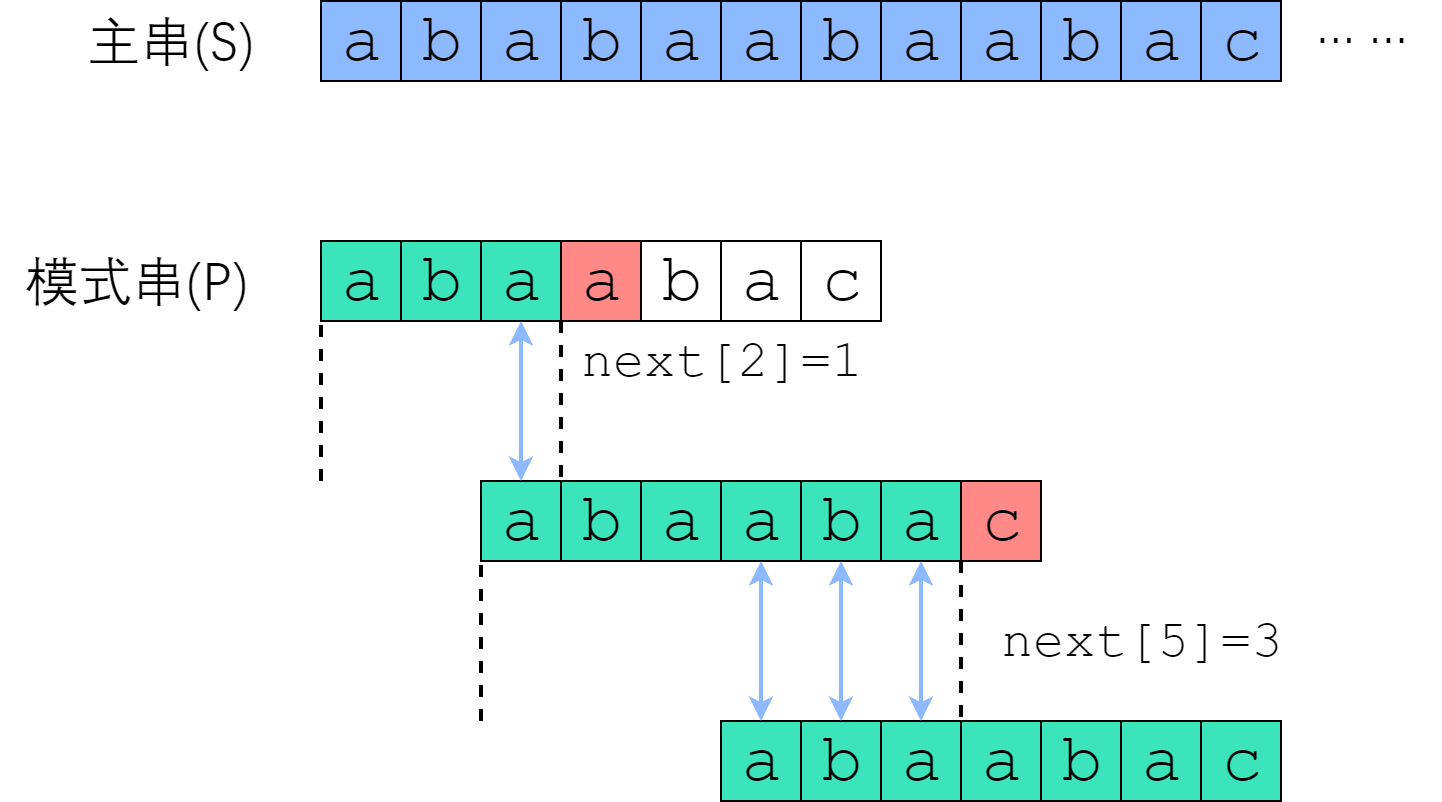
在 S[0] 尝试匹配,失配于 S[3] <=> P[3] 之后,我们直接把模式串往右移了两位,让 S[3] 对准 P[1]. 接着继续匹配,失配于 S[8] <=> P[6], 接下来我们把 P 往右平移了三位,把 S[8] 对准 P[3]. 此后继续匹配直到成功。
我们应该如何移动这把标尺?很明显,如图中蓝色箭头所示,旧的后缀要与新的前缀一致(如果不一致,那就肯定没法匹配上了)!
回忆next数组的性质:P[0] 到 P[i] 这一段子串中,前next[i]个字符与后next[i]个字符一模一样。既然如此,如果失配在 P[r], 那么P[0]~P[r-1]这一段里面,前next[r-1]个字符恰好和后next[r-1]个字符相等——也就是说,我们可以拿长度为 next[r-1] 的那一段前缀,来顶替当前后缀的位置,让匹配继续下去!
您可以验证一下上面的匹配例子:P[3]失配后,把P[next[3-1]]也就是P[1]对准了主串刚刚失配的那一位;P[6]失配后,把P[next[6-1]]也就是P[3]对准了主串刚刚失配的那一位。

如上图所示,绿色部分是成功匹配,失配于红色部分。深绿色手绘线条标出了相等的前缀和后缀,其长度为next[右端]. 由于手绘线条部分的字符是一样的,所以直接把前面那条移到后面那条的位置。因此说,next数组为我们如何移动标尺提供了依据。接下来,我们实现这个优化的算法。
(2)利用next数组进行匹配
了解了利用next数组加速字符串匹配的原理,我们接下来代码实现之。分为两个部分:建立next数组、利用next数组进行匹配。
首先是建立next数组。我们暂且用最朴素的做法,以后再回来优化:

如上图代码所示,直接根据next数组的定义来建立next数组。不难发现它的复杂度是 O(m^2) 的。
接下来,实现利用next数组加速字符串匹配。代码如下:

如何分析这个字符串匹配的复杂度呢?乍一看,pos值可能不停地变成next[pos-1],代价会很高;但我们使用摊还分析,显然pos值一共顶多自增len(S)次,因此pos值减少的次数不会高于len(S)次。由此,复杂度是可以接受的,不难分析出整个匹配算法的时间复杂度:O(n+m)。
5、快速求next数组
终于来到了我们最后一个问题——如何快速构建next数组。
首先说一句:快速构建next数组,是KMP算法的精髓所在,核心思想是“P自己与自己做匹配”。
为什么这样说呢?回顾next数组的完整定义:
- 定义 “k-前缀” 为一个字符串的前 k 个字符; “k-后缀” 为一个字符串的后 k 个字符。k 必须小于字符串长度。
- next[x] 定义为: P[0]~P[x] 这一段字符串,使得k-前缀恰等于k-后缀的最大的k.
这个定义中,不知不觉地就包含了一个匹配——前缀和后缀相等。接下来,我们考虑采用递推的方式求出next数组。如果next[0], next[1], ... next[x-1]均已知,那么如何求出 next[x] 呢?
来分情况讨论。首先,已经知道了 next[x-1](以下记为now),如果 P[x] 与 P[now] 一样,那最长相等前后缀的长度就可以扩展一位,很明显 next[x] = now + 1. 图示如下。

刚刚解决了 P[x] = P[now] 的情况。那如果 P[x] 与 P[now] 不一样,又该怎么办?

如图。长度为 now 的子串 A 和子串 B 是 P[0]~P[x-1] 中最长的公共前后缀。可惜 A 右边的字符和 B 右边的那个字符不相等,next[x]不能改成 now+1 了。因此,我们应该缩短这个now,把它改成小一点的值,再来试试 P[x] 是否等于 P[now].
now该缩小到多少呢?显然,我们不想让now缩小太多。因此我们决定,在保持“P[0]~P[x-1]的now-前缀仍然等于now-后缀”的前提下,让这个新的now尽可能大一点。 P[0]~P[x-1] 的公共前后缀,前缀一定落在串A里面、后缀一定落在串B里面。换句话讲:接下来now应该改成:使得 A的k-前缀等于B的K-后缀的最大的k.
您应该已经注意到了一个非常强的性质——串A和串B是相同的!B的后缀等于A的后缀!因此,使得A的k-前缀等于B的k-后缀的最大的k,其实就是串A的最长公共前后缀的长度 —— next[now-1]!

来看上面的例子。当P[now]与P[x]不相等的时候,我们需要缩小now——把now变成next[now-1],直到P[now]=P[x]为止。P[now]=P[x]时,就可以直接向右扩展了。
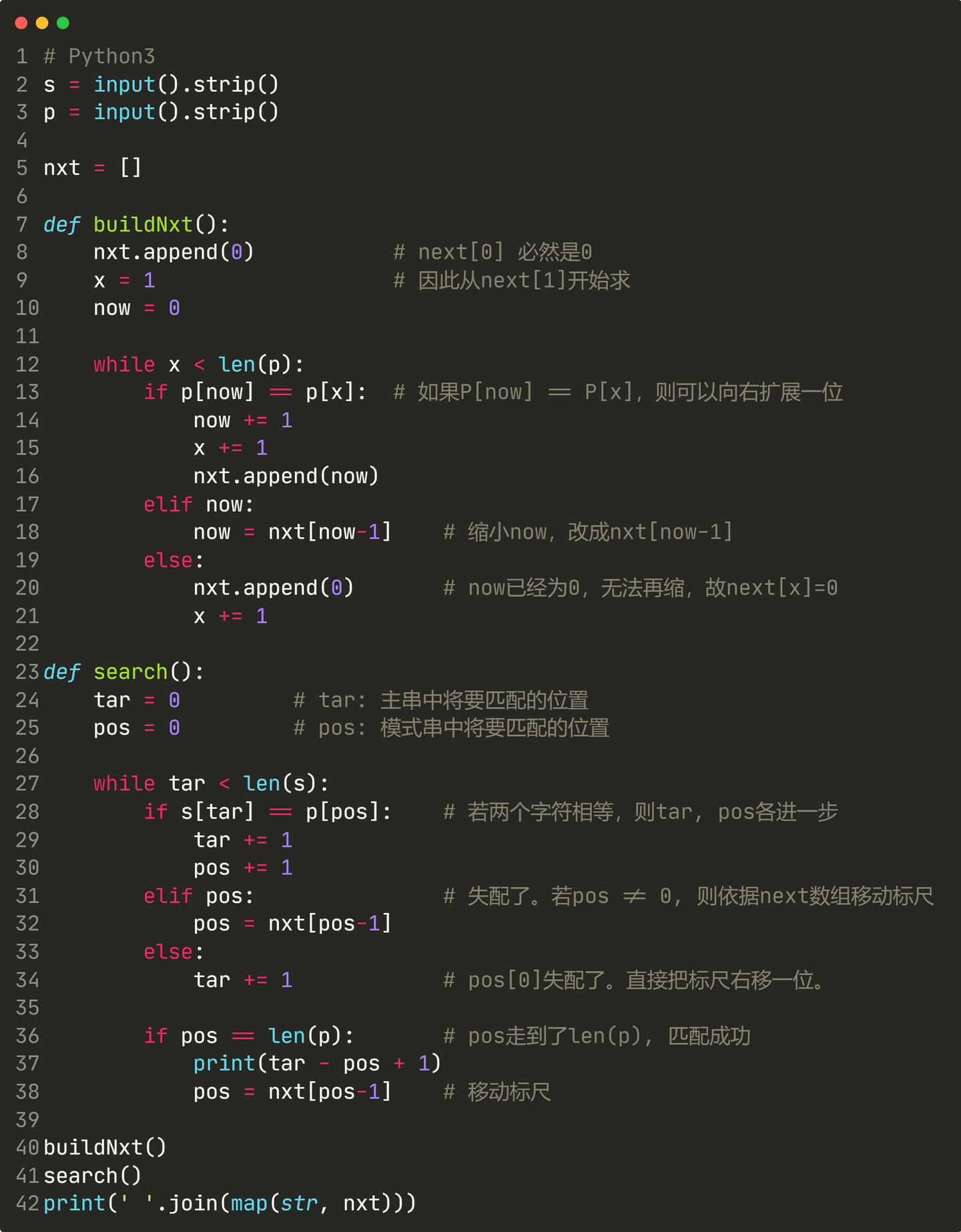
代码实现如下:

应用摊还分析,不难证明构建next数组的时间复杂度是O(m)的。至此,我们以O(n+m)的时间复杂度,实现了构建next数组、利用next数组进行字符串匹配。
以上就是KMP算法。它于1977年被提出,全称 Knuth–Morris–Pratt 算法。最后附上KMP算法字符串匹配的Python和Java版代码:









![[JS设计模式]Mixin Pattern](https://img-blog.csdnimg.cn/direct/e05e77271f1d4b30a549c72f31785d33.png)
![[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set)](https://img-blog.csdnimg.cn/direct/c21ecbf9766745369e878ecba1c82a5d.png)
