---

前言

路漫漫其修远兮，吾将上下而求索，在上次内容中小编介绍了有关于操作符的基本知识，但是操作符用来干什么的呢？毫无置疑操作符使用于表达式，在本次内容中小编将会带大家学习一下表达式的优先级和结合性，虽然该章内容设计知识是需要记的，但是还是一句话：熟能生巧，实践出真知，我们只有不断的写代码才能记住这些内容，而不是去死记硬背。好啦不多唠嗑了，开始我们的新内容吧，go go go！！！

---

提示：以下是本篇文章正文内容，下面案例可供参考

一，操作符的属性

复杂表达式的求值有三个影响的因素
1，操作符的优先级
2，操作符的结合性
3，是否控制求值顺序
两个相邻的操作符先执行优先级高的，如果两者的优先级相同，取决于他们的结合性。

接下来就通过下面这个表达式来引出大家对于这个问题的疑惑吧：下面表达式在计算机中的运算过程是怎么样的。而通过学习操作符的属性可以判断自己写的代码是否存在逻辑上的bug。

int main()
{
	int x = 3 + 3 * 4 + 6;
	return 0;
}

二、1，表达式求值的优先级

1，什么是优先级

优先级指的是，如果一个表达式包含多个运算符，优先级高的运算符先执行。各种操作符的优先级是不同的。

2，表达式的优先级表格

在这里重点看到我黑体的那些

操作符	名称
（）	聚组，也被称为括号
（）	函数调用
[ ]	下标引用
.	访问结构成员
->	访问结构指针成员
++	后置++
–	后置–
！	逻辑反
~	按位取反
+	单目操作符，表示正值
-	单目操作符，表示负值
++	前置++
–	前置–
*	间接访问
&	取地址
sizeof	求长度，单位字节
（类型）	类型转换
*	乘法
/	除法
%	取余操作符（只能是整数）
+	加法
-	减法
<<	左移
>>	右移
>	大于
<	小于
==	等于
！=	不等于
&	按位与
^	按位异或
	按位或
&&	逻辑与
	逻辑或
	三目操作符
=	赋值
，	逗号

分析

具体参考 表达式优先级表格，在这里我们可以发现赋值优先级几乎是处于最低的，在上面表格中在我们平常编译中常用的就是上面黑体部分的。具体其他的可以参考小编给的链接加以理解，接下来小编带大家熟悉一点操作符的优先级

int main()
{
	int x = 2 + 6 / 3; 
	return 0;
}

分析

在该表达式中，乘法的优先级高于加法优先级，所以先执行乘法，然后在执行加法，最后执行赋值运算

三、表达式的结合性

1，什么是表达式的结合性

如果两个表达式优先级相同，优先级没办法确定先执行哪个，这时候就看结合性了，则根据运算符是做结合还是右结合，决定执行顺序。大部分运算符是左结合（也即是从左向右计算），少数运算符是从右向左计算，比如赋值操作符，下面就介绍一些操作符的结合性吧

2，表达式的结合性表格

操作符	结合性
（）	无结合性
后置++	从左向右
后置 - -	从左向右
！	从右向左
~	从右向左
前置++	从右向左
前置–	从右向左
乘法	从左向右
/	从左向右
%	从左向右
+	从左向右
-	从左向右
<<	从左向右
>>	从左向右
小于，等于，大于，不等于	从左向右
&	从左向右
^	从左向右
按位或	从左向右
&&	从左向右
逻辑或	从左向右
=	从右向左
，	从左向右

#include<stdio.h>      
int main()      
{
	int y = 2 + 3 + 4; //优先级情况相同的话就要考虑结合性的问题      
	return 0;      
}

分析

在这里都是加号，优先级相同的情况下考虑结合性，加法的结合性是从左向右的所以，先2+3然后最后加上4，然后赋值优先级是从右向左，所以把加法所得的总值赋值给了y。

---

四，隐式类型转换

1，什么叫整型提升？

注意整型提升是一个表达式里面的类型达不到整型大小的char和short类型才会整型提升

1,表达式求值的顺序一部分是由操作符的优先级和结合性决定
2,同样，有些表达式的操作数在求值的过程中可能需要转换成其他类型
3,c的整型运算总是至少以默认整型类型的精度进行的
4,为了获得这个精度，表达式中的字符和短整型操作数在使用之前会被转换为普通整型，这种转换被称为整形提升

证明整型提升如下：

int main()
{
	char a = 3;
	printf("%d\n", sizeof(a));
	printf("%d\n", sizeof(+a));
	printf("%d\n", sizeof(-a));
	return 0;
}

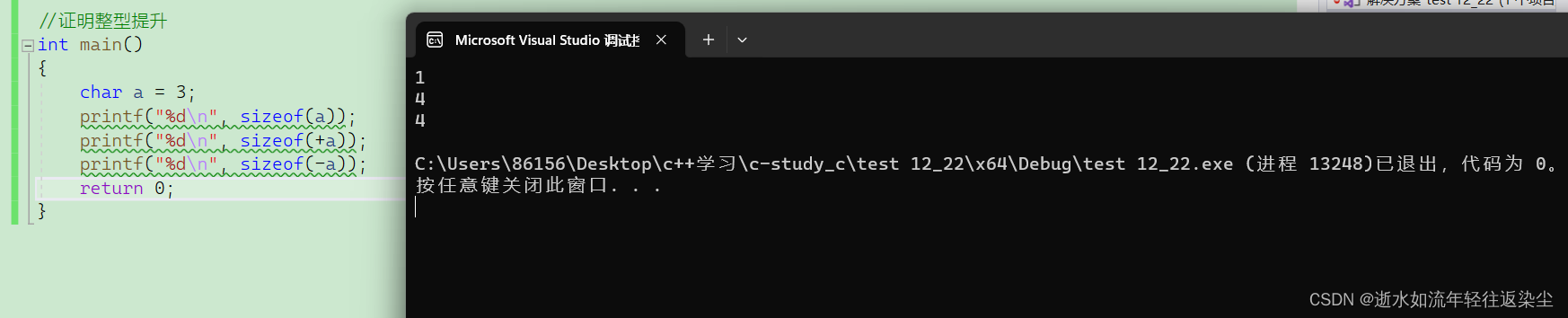
分析

在这里可以看到第一个，sizeof操作符求解的第一个为字符变量a的字节大小，为1个字节；按照道理字符变量的运算得到最后的结果还是字符变量字节为1，但是第二个第三个最后得到值为4个字节，这是因为第二个和第三个为字符变量参与了表达式运算，c的整型运算总是至少以默认整型类型的精度进行的，但是为了获得这个精度，表达式中的字符和短整型操作数在使用之前会被转换为普通整型也就是整型提升由一个字节转换为四个字节。

int main()
{
	//隐式类型转换
	char a = 5;
	char b = 126;
	char c = a + b;
	printf("%d\n",c);
	return 0;
}

分析

在这里a是字符型，b也是字符型，char类型的数据在做运算之前（这里指加法）我们得先把a和b转换为普通整型，然后让它进行加法运算。这是为啥呢？因为表达式的整型运算在cpu的相应运算器内执行，cpu内整型运算器的操作数的字节长度一般是int的字节长度同时也是cpu的通用寄存器的长度。因此，即使两个char类型的相加，在cpu执行时实际也要先转换为cpu内整型操作数的标准长度。通用cpu是难以直接实现两个8比特也就是一个字节直接相加运算。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入cpu去执行运算。

2，如何整型提升？

整型提升是按照变量的数据类型来提升的

int main()     
{
	//负数整型提升     
	char c1 = -1;     
	char c2 = 1;     
	return 0;     
}

分析

首先-1在内存中存储的是二进制位的补码形式32个比特位，而变量c1的二进制位（补码）只有8个比特位，所以发生了截断，取了后面的八个比特位11111111，假如要对c1进行整型提升，在这里c1是有符号字符型，所以我们默认他的最高位为符号位，要进行整型提升，所以要把它变为整型类型32个比特位，则剩下缺的用符号位来补上。第二个c2为正数，和负数一样截断取八位，最后整型提升用符号位补齐。也就是用0补齐。而无符号整型提升，高位直接补零。

3，习题练习

1，求解c的大小

int main()
{
	char a = 5;
	char b = 126;
	char c = a + b;
	printf("%d\n", c);
	return 0;
}

分析

首先a是字符变量5，b是字符变量126，在进行a加b的运算中，先要将a和b转换为整型大小，也就是整型提升，最高位用符号位补齐得到下图；然后得到c的值但是c是字符型变量于是发生截断，得到八位数也就是八个比特位，运行到下一步骤，在这里需要以%d的形式进行打印，于是需要整型提升，但是此时最高位为1也就是代表他的符号位，然后整型提升剩下用1补齐，此时得到反码将之转换为原码转换成十进制得到-125。 

2，整型提升的例子

int main()
{
	char a = 0xb6;
	//10110110 整型提升这里最高位默认为1所以剩下的用0补齐
	short b = 0xb600;
	//1011011000000000
	int c = 0xb6000000;
	if (a == 0xb6)
		printf("a");
	if (b = 0xb600)
		printf("b");
	if (c = 0xb6000000)
		printf("c");
	return 0;
}

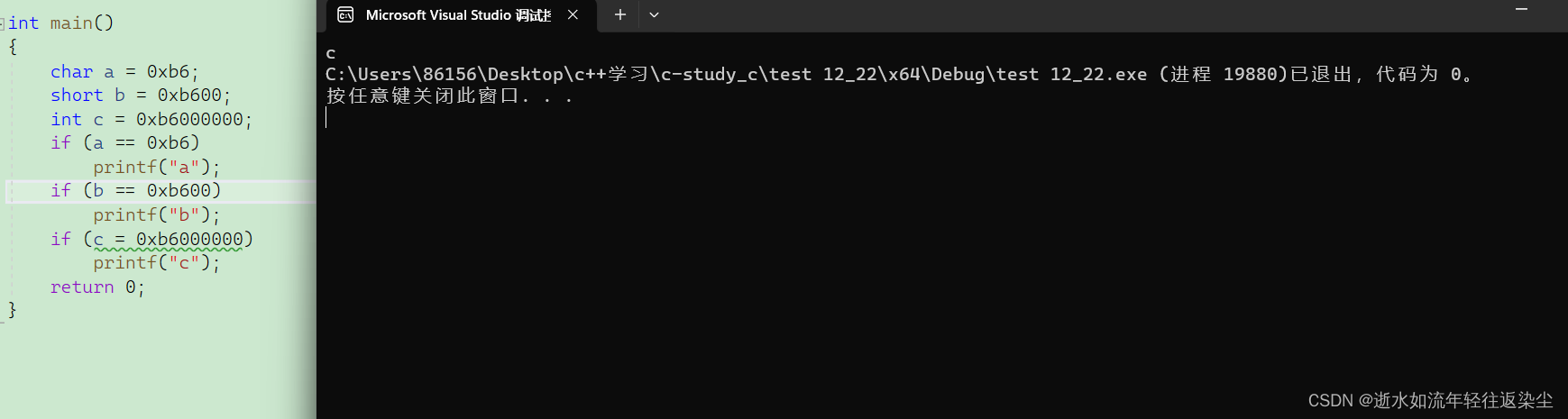
分析

在这里例子中的a和b要进行整型提升，但是c不需要进行整型提升，a和b整型提升后变成了负数，所以表达式a==0xb6，b=0xb600的结果是假，但是c不发生整型提升，所以表达式c=0xb6000000的结果为真。最终结果就执行了第三个判断语句后面的结果。

4，算数转换

算数转换是那些类型大于等于整型大小的类型进行表达式运算的隐式转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的为寻常算术转换

操作数类型	字节大小
long double	8
double	8
float	4
unsigned long int	4
long int	4
unsigned int	4
int	4

在这里如果操作数的类型在上面的表格较低，那么首先要转换为另外一个操作数的类型后执行运算，也就是说如果包含int和float要转换为float类型进行运算

五，求值顺序

在这里求值顺序就几个我给大家列出来

操作符	名称
&&	逻辑与
	逻辑或
	三目操作符
，	逗号表达式

分析

在这里为啥会影响，在这之前小编讲述了有关与c语言操作符的知识： 详解c语言操作符（下篇），关于逻辑与操作符我们判断之前如果有假的话后面语句就不再执行，这就是影响了求值顺序，本来逻辑与操作符执行顺序是从左到右依次执行但是只要出现假的话后面语句就不会再执行了。同样的逻辑或也是一样的原理。对于三目操作符，表达式1为真，表达式2计算，表达式3不计算选择性的执行表达式的内容。逗号表达式从左向右依次计算，但是真正取到决定性作用的是最后一个表达式的结果，最后一个表达式的结果是整个表达式的结果。

---

总结

我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径，那这个表达式就是存在问题的。
以上就是今天要讲的内容，本文仅仅简单介绍了表达式求值的优先级和结合性，而具体使用和记忆得各位读者在日常代码中了，学习不是一蹴而就的活，小编只是简单介绍了表达式求值的过程中遇到的相关计算，如果各位读者忘记了能有资料回头看看就收藏一下吧。