题目链接
P1883 函数
思路
举例
题目中的 F ( x ) F(x) F(x) 看起来很复杂,但由于每个 f ( x ) f(x) f(x) 的二次项系数 a a a 都不是负数,故 F ( x ) F(x) F(x) 是一个单谷函数。直接说出结论可能有些令人难以接受,不妨举出两个例子。
第一个例子是
a
a
a 大于0的情况,即
f
1
(
x
)
=
x
2
,
f
2
(
x
)
=
x
2
−
2
x
+
10
f_1(x)=x^2,f_2(x)=x^2-2x+10
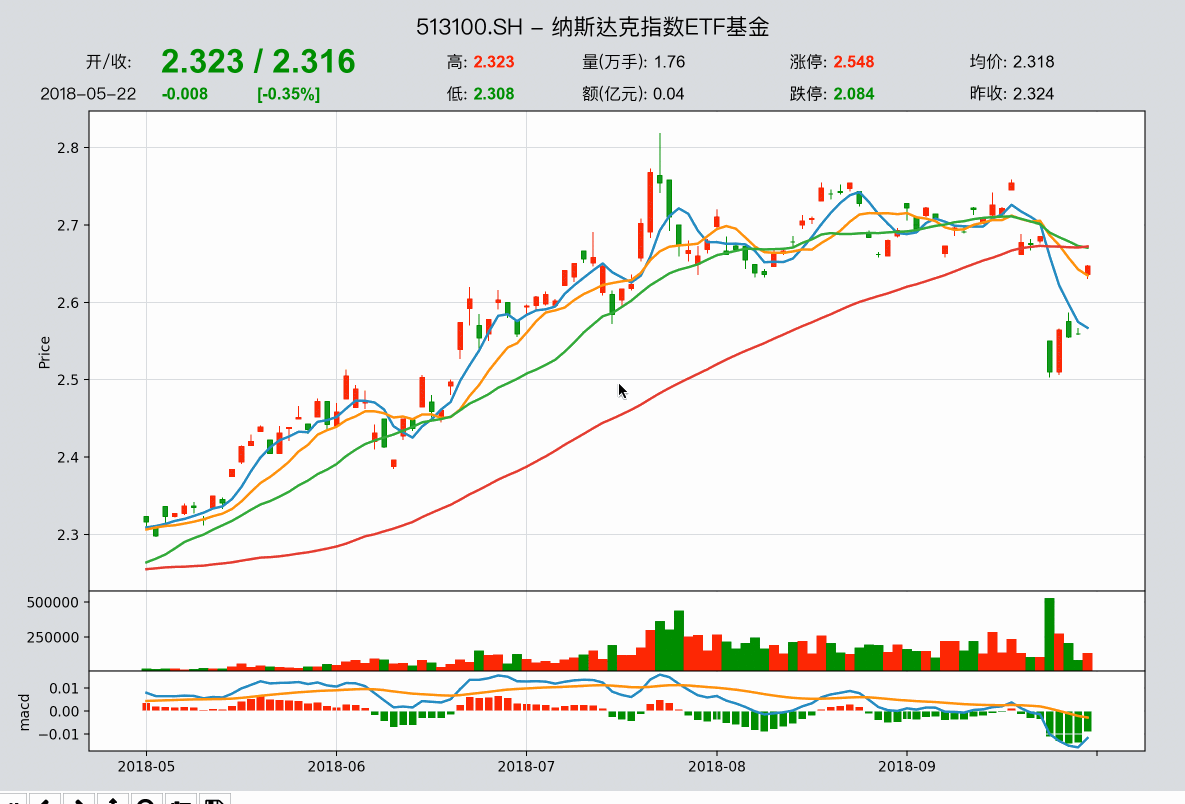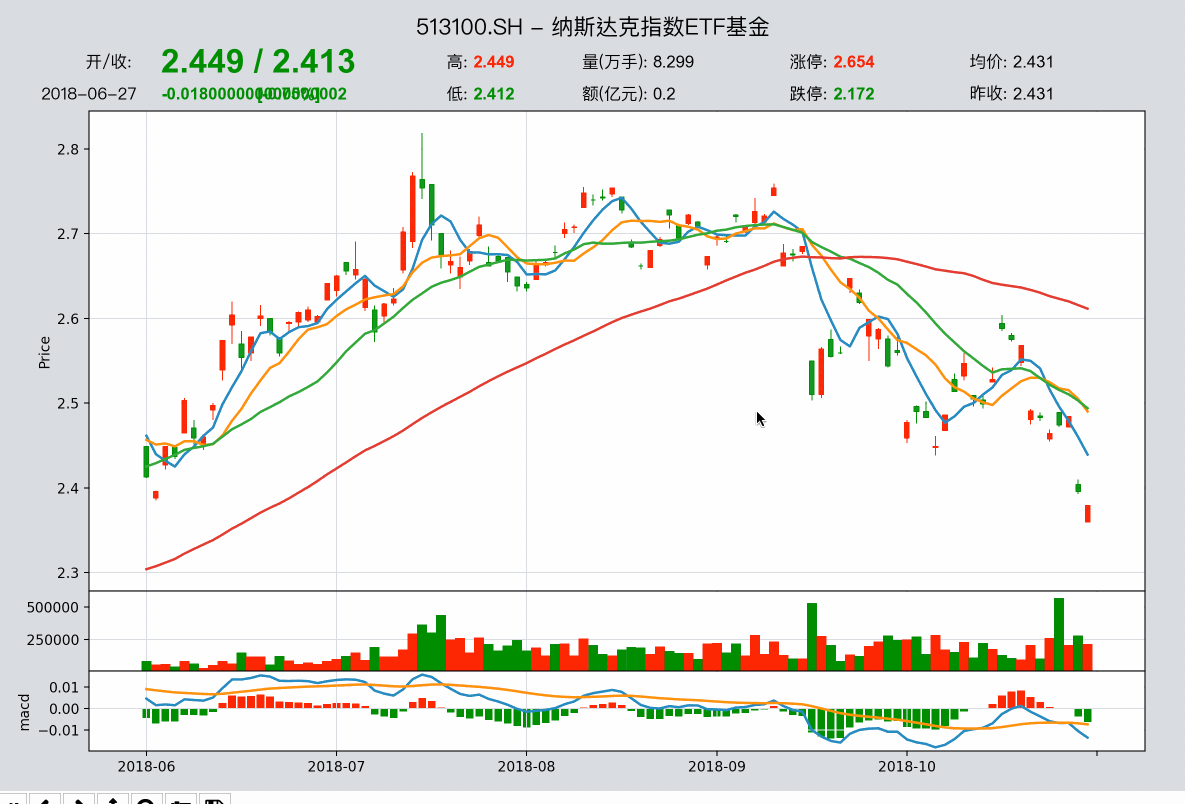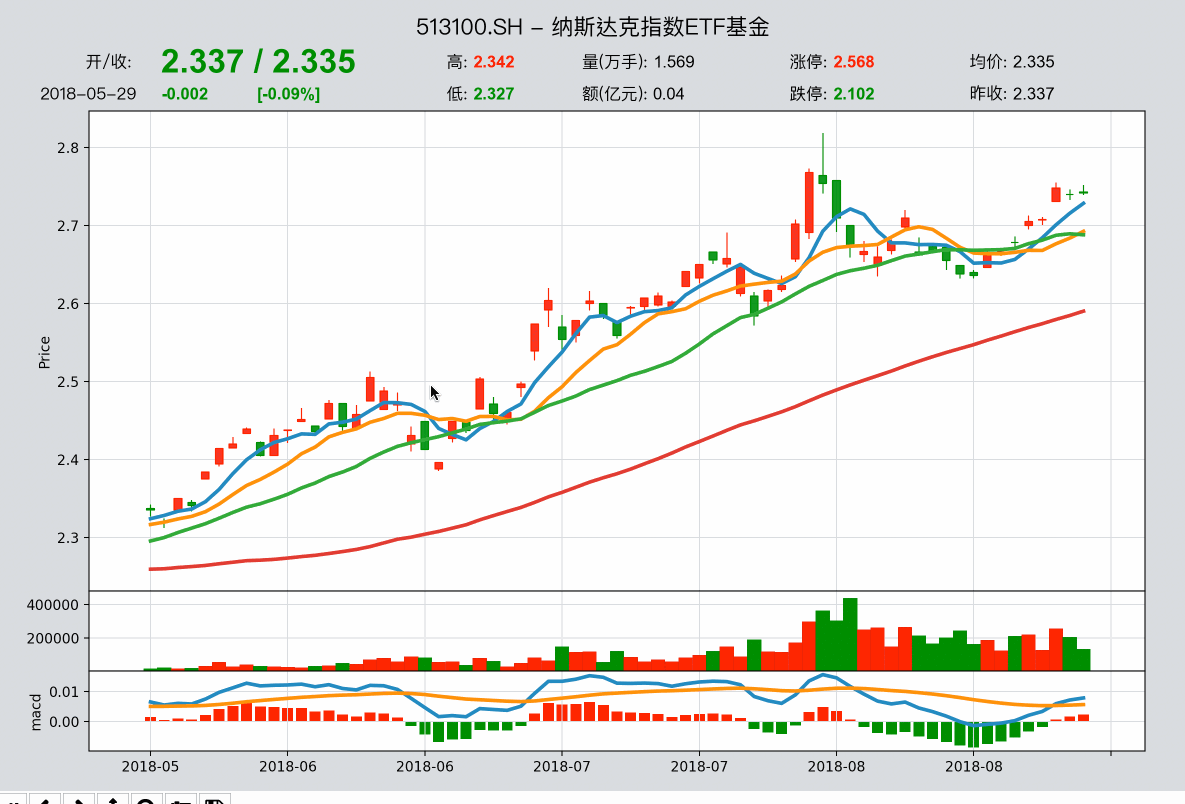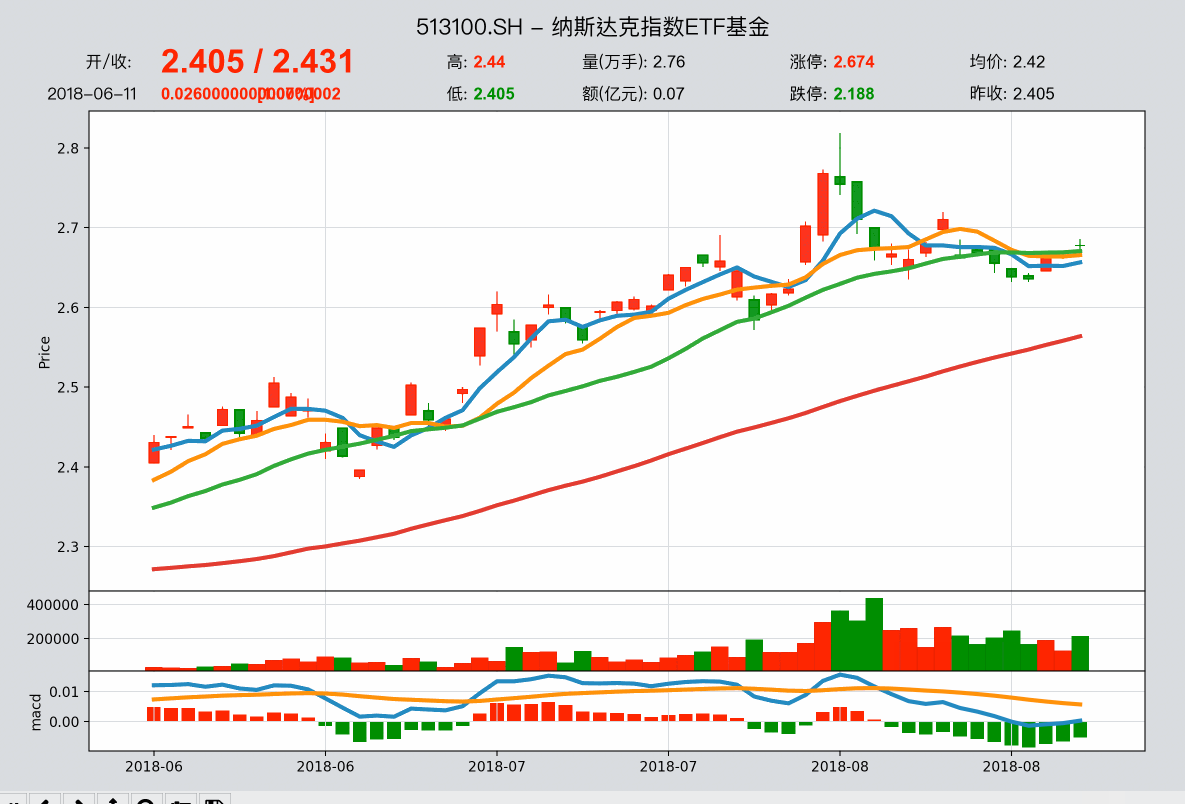
f1(x)=x2,f2(x)=x2−2x+10 ,图像如下:

显然,当 x ≥ 5 x≥5 x≥5 时, f 1 ( x ) ≥ f 2 ( x ) f_1(x)≥f_2(x) f1(x)≥f2(x) ;当 0 ≤ x < 5 0≤x<5 0≤x<5 时, f 1 ( x ) < f 2 ( x ) f_1(x)<f_2(x) f1(x)<f2(x) 。所以在区间 [ 0 , 5 ) [0, 5) [0,5) 上, F ( x ) F(x) F(x) 取 f 2 ( x ) f_2(x) f2(x) 的函数值;所以在区间 [ 5 , 1000 ] [5, 1000] [5,1000] 上, F ( x ) F(x) F(x) 取 f 1 ( x ) f_1(x) f1(x) 的函数值。显然 F ( x ) F(x) F(x) 的图像是一个单谷函数,有最小值。
第二个例子是
a
a
a 等于0的情况,即
f
1
(
x
)
=
x
2
,
f
2
(
x
)
=
x
+
2
f_1(x)=x^2,f_2(x)=x+2
f1(x)=x2,f2(x)=x+2 ,图像如下:

显然,当 x ≥ 2 x≥2 x≥2 时, f 1 ( x ) ≥ f 2 ( x ) f_1(x)≥f_2(x) f1(x)≥f2(x) ;当 0 ≤ x < 2 0≤x<2 0≤x<2 时, f 1 ( x ) < f 2 ( x ) f_1(x)<f_2(x) f1(x)<f2(x) 。所以在区间 [ 0 , 2 ) [0, 2) [0,2) 上, F ( x ) F(x) F(x) 取 f 2 ( x ) f_2(x) f2(x) 的函数值;所以在区间 [ 2 , 1000 ] [2, 1000] [2,1000] 上, F ( x ) F(x) F(x) 取 f 1 ( x ) f_1(x) f1(x) 的函数值。显然 F ( x ) F(x) F(x) 的图像是一个单谷函数,有最小值。
通过以上两个例子,可推得只要 a ≥ 0 a≥0 a≥0 那么无论增加多少个二次函数(或者退化为一次函数),最终形成的函数 F ( x ) F(x) F(x) 势必是一个单谷函数,有最小值,故想到使用三分法求最小值。
三分法
对于初始的区间,左端点 l e f t left left 为0,右端点 r i g h t right right 为1000,左三等分点 m i d L midL midL 和右三等分点 m i d R midR midR 在循环中更新。
如果 F ( m i d L ) > F ( m i d R ) F(midL) > F(midR) F(midL)>F(midR) ,说明函数的最小值点在区间 [ m i d L , r i g h t ] [midL, right] [midL,right] ,故更新 l e f t left left 到 m i d L midL midL ;否则说明函数的最小值点在区间 [ l e f t , m i d R ] [left, midR] [left,midR] ,故更新 r i g h t right right 到 m i d R midR midR 。如果不理解三分的更新子区间,请参考算法——三分法。
当区间长度小于指定精度 p r e c i s i o n precision precision 时,退出循环,输出结果。详见代码。
使用inline
题解中使用了关键字 i n l i n e inline inline ,只要一个函数被 i n l i n e inline inline 修饰(这种函数被称为内联函数),那么使用该函数的地方会粘贴函数体里面的代码,从而加快函数的调用,并且减少栈空间的浪费。求 f 1 ( x ) , f 2 ( x ) , . . . , f n ( x ) f_1(x), f_2(x),...,f_n(x) f1(x),f2(x),...,fn(x) 的函数值被使用了很多次,故使用内联函数加快执行速度。
代码
#include <iostream>
#include <cstdio>
using std::cin, std::cout;
const int N = 1e4 + 5; // 数组长度
const double precision = 1e-9; // 精度
/*
n是二次函数的个数 a[]保存二次项系数
b[]保存一次项系数 c[]保存常数项
*/
int n, a[N], b[N], c[N];
inline double func(double x, int num) { // 求第num个二次函数在x处的取值
return a[num] * x * x + b[num] * x + c[num];
}
double getFuncMax(double x) { // 求F(x)在x处的取值
double res = func(x, 0);
for (int i = 1; i < n; i++) {
double temp = func(x, i);
res = res > temp ? res : temp;
}
return res;
}
void process() { // 每个测试案例的解决方案
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i] >> b[i] >> c[i];
}
double left = 0.0, right = 1000.0, midL, midR;
while (right - left > precision) {
midL = left + (right - left) / 3.0;
midR = right - (right - left) / 3.0;
if (getFuncMax(midL) > getFuncMax(midR)) {
left = midL;
} else {
right = midR;
}
}
printf("%.4lf\n", getFuncMax(left)); // left是F(x)的最小值点
}
int main() {
int t; // 测试案例的个数
cin >> t;
while (t-- > 0) {
process();
}
return 0;
}
说明
本文的两个函数图像由 G e o G e b r a GeoGebra GeoGebra 生成。