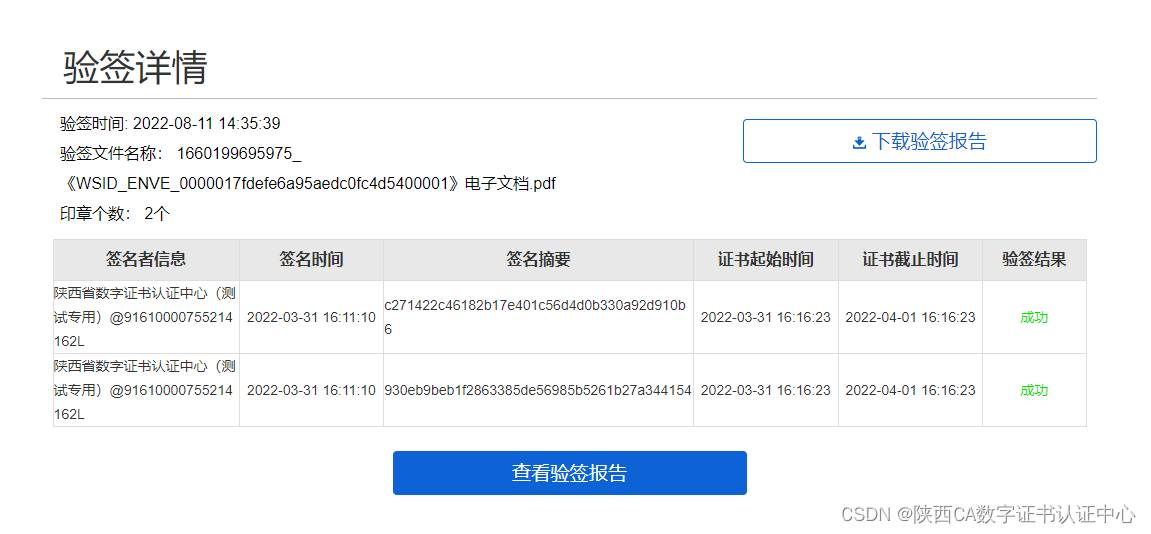
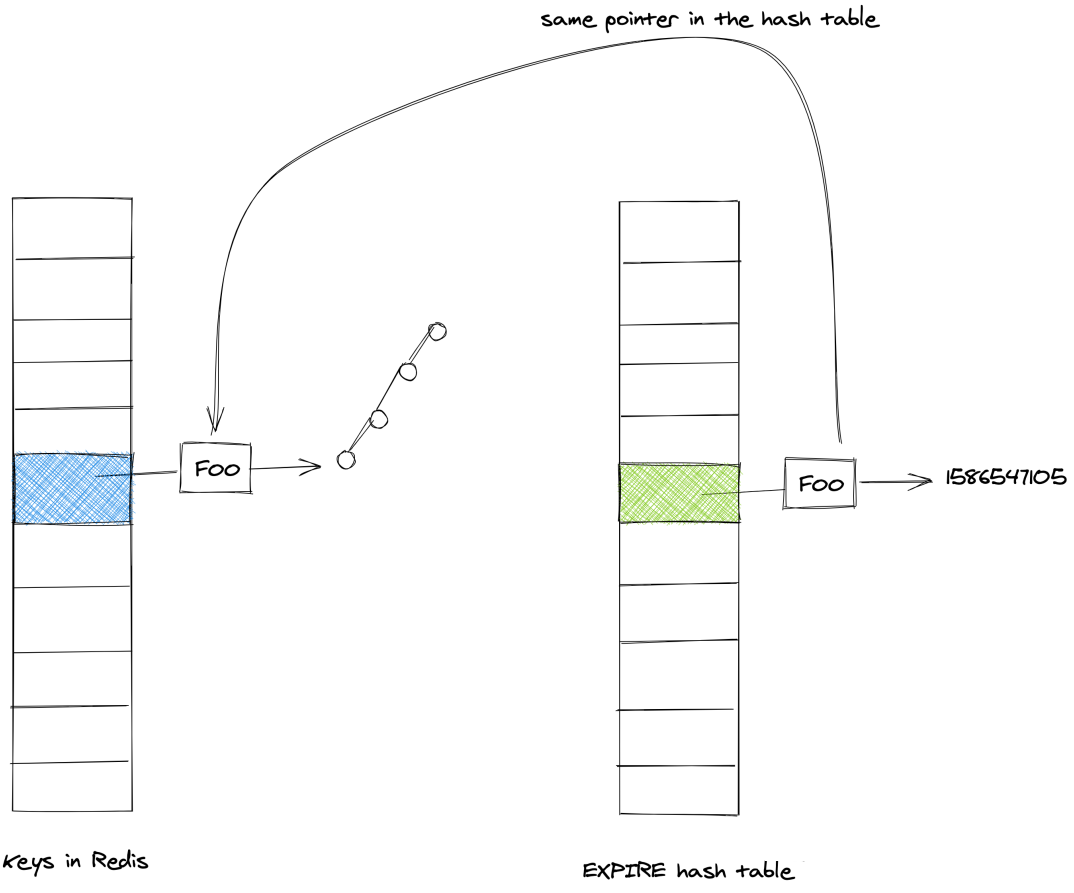
就像学习其他的东西一样，首先我们要知道二叉搜索树的作用和定义是什么！

首先顾名思义，二叉搜索树肯定是被用来为搜索服务的数据结构。

并且它的搜索效率可以达到logN,也就是一百万的数据也只用查找几十次（AVL树可以控制在20次左右，红黑树可以控制在20到40次之间）

那么接下来我们就了解它是如何实现这一神奇操作的。

首先我们给出二叉搜索树的定义。（首先知道二叉树）

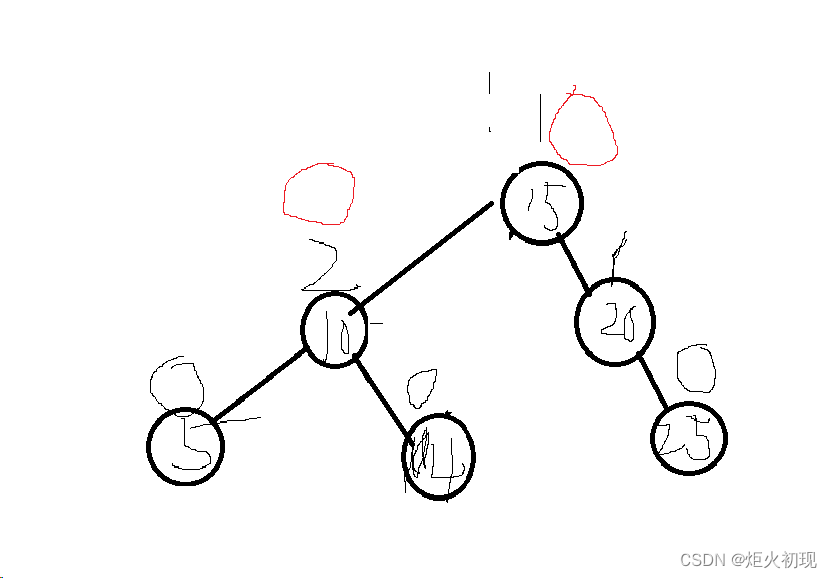
二叉搜索树就是让二叉树的左节点一定小于父节点，右节点一定大于夫节点。

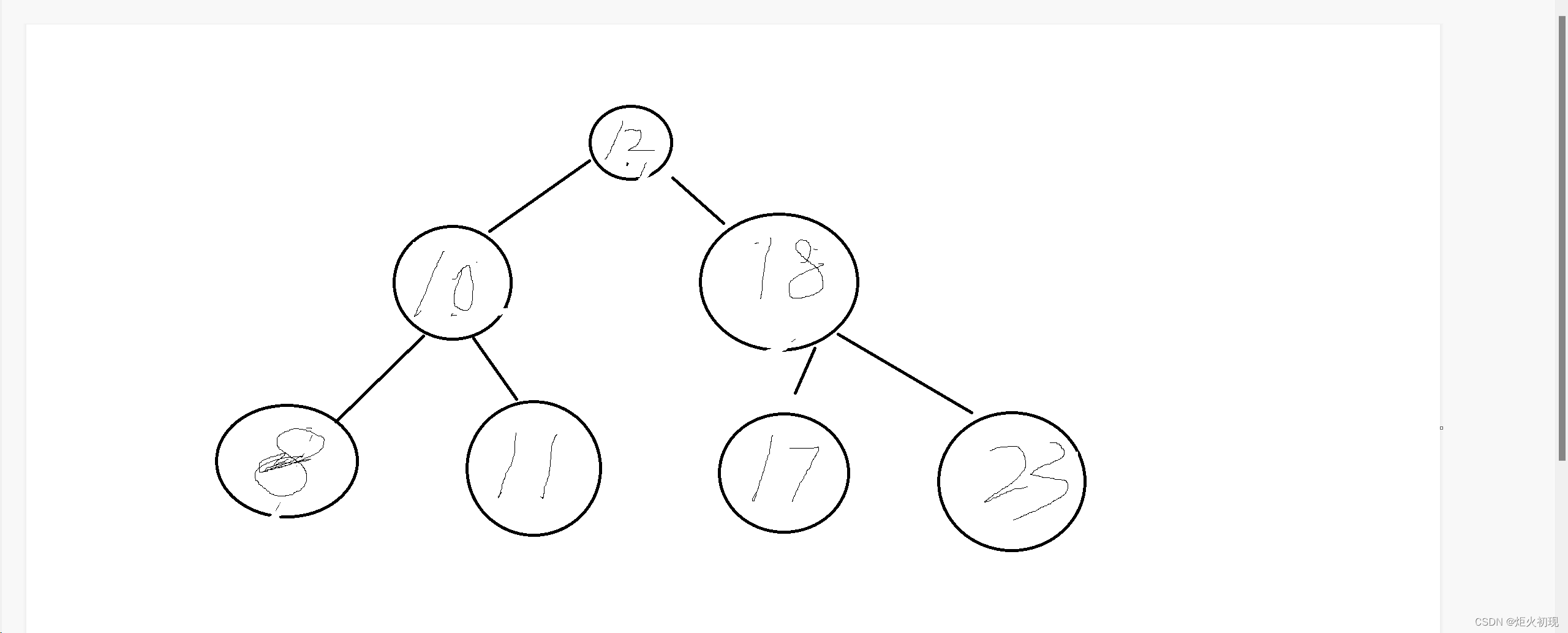
比如这张图就是一个平衡二叉树。

接下来我们看实现的代码。

首先是一棵树的基本组成结构左节点，右节点，还有节点的数据

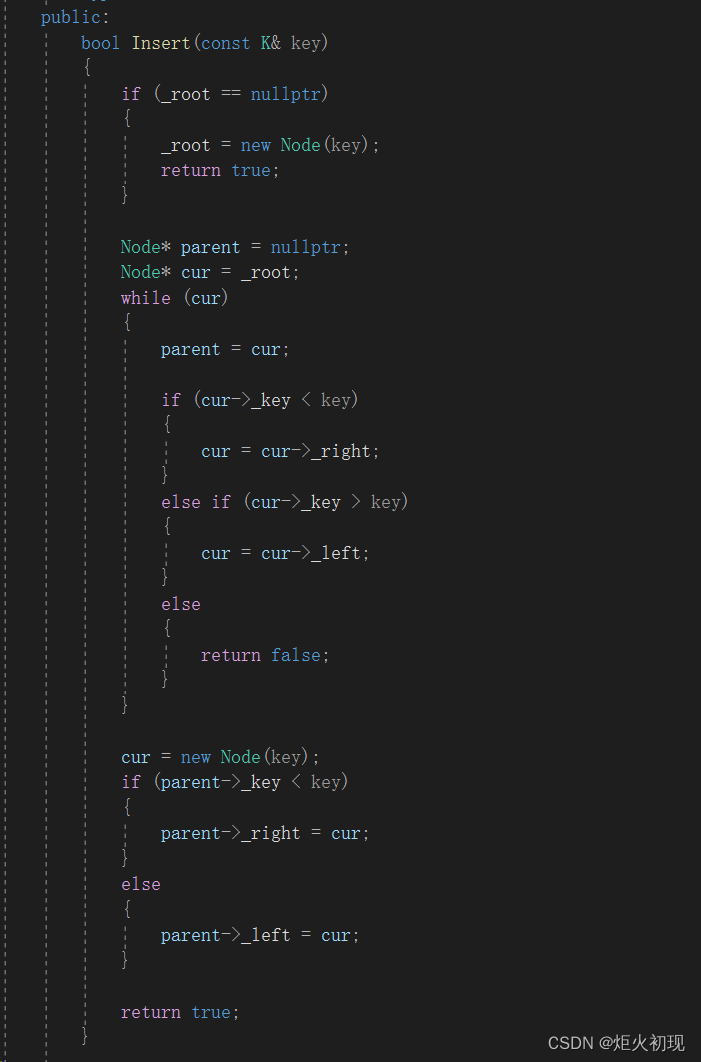
首先是如果这是根节点那就直接创建然后返回就可以了。

然后如果不是根节点，那我们就要先找到正确的位置再进行插入。

那么这个时候我们可以先用一个cur指针去进行寻找。

通过值的大小选择不同的走向，一直到遇到一颗树正确的根节点的正确插入位置。（其实就是让父节点达到正确的叶节点）

然后插入。但是我们要实现链接所以，我们必须要记录一下父节点的位置，这样才能让我进行链接。

  

然后通过判断选择正确的左右方向插入即可。

找到的实现基本同理，主要也是向下寻找即可。

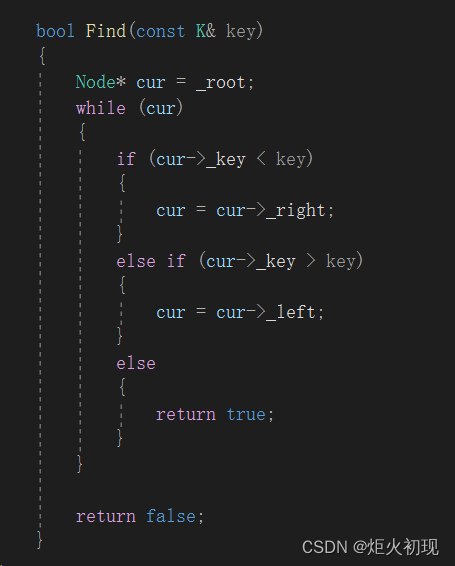
接下来我们来研究删除！

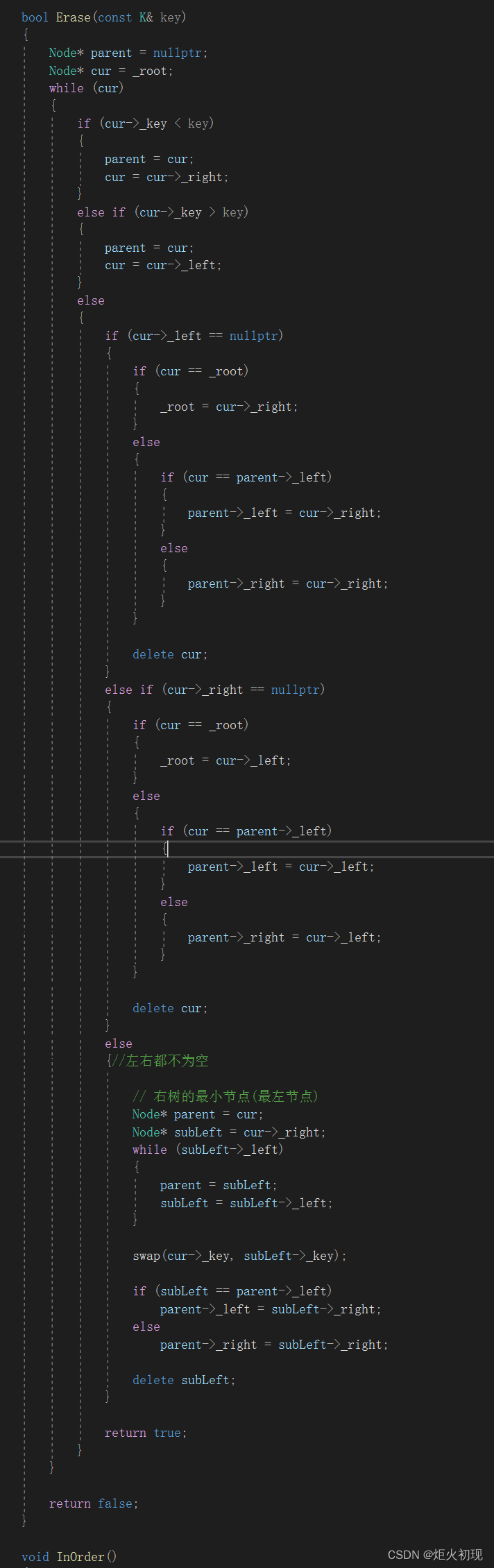
删除的第一步肯定还是先要找到才能删除

那么如果要找的值大于当前节点的值就找右边，反正就找左边。

如果cur找到了空节点任然没有相等的则直接跳出循环，返回false即删除失败，如果找到了

则开始删除的程序。

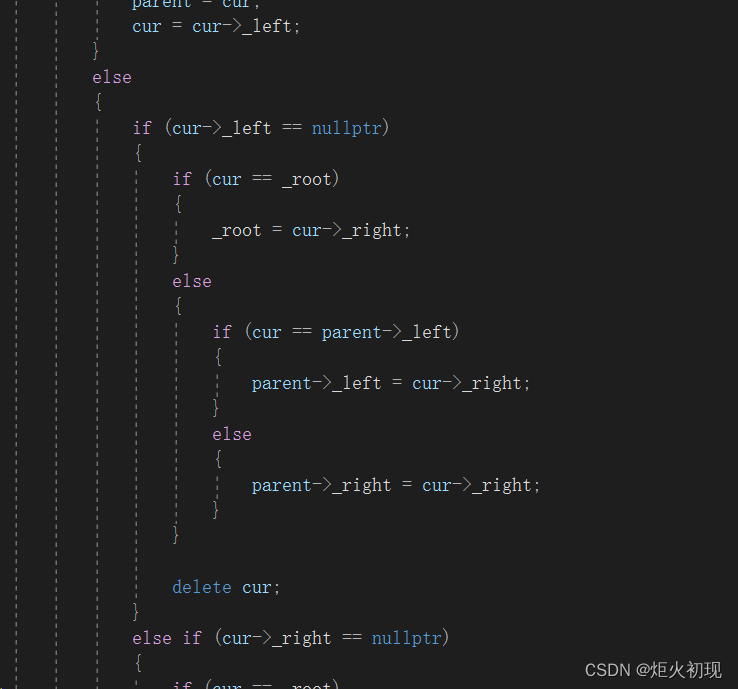
首先如何找到的节点如果左子树为空并且cur节点为父节点的左边，那我们就把右子树与父节点链接起来。反正就连接左子树与夫节点。当我们重新连接完树以后就可以删除节点的数据了。

当然有一种特殊情况就是如果删除的节点是根节点，那么我们就把根节点移交出去即可。

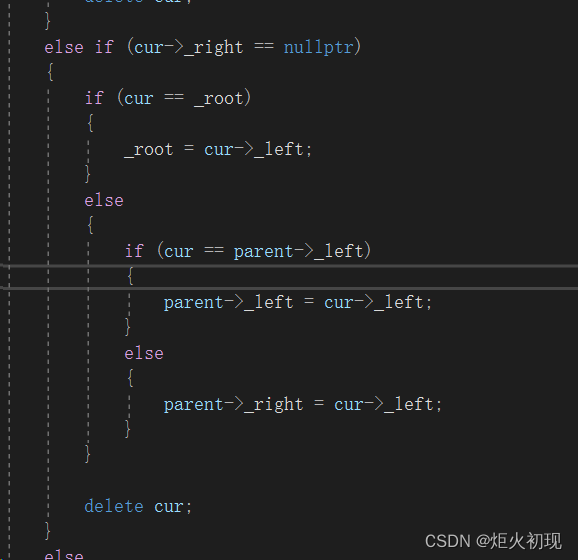
如果右子树为空是同理的。

接下来如果是左右都不为空。

那么我们显然就不能直接重新连接然后删除了。

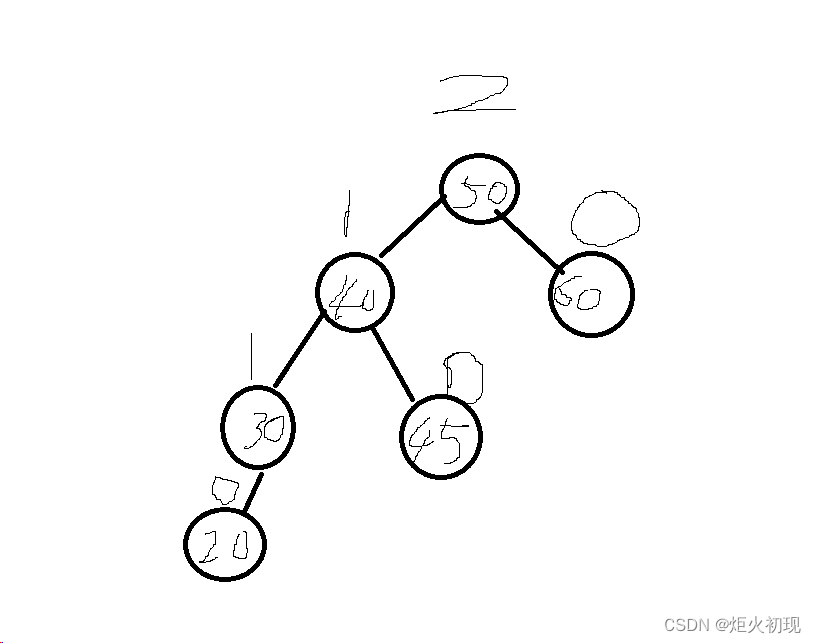
比如下图

如果删除了10，那么无论如何连接都很难再恢复平衡。

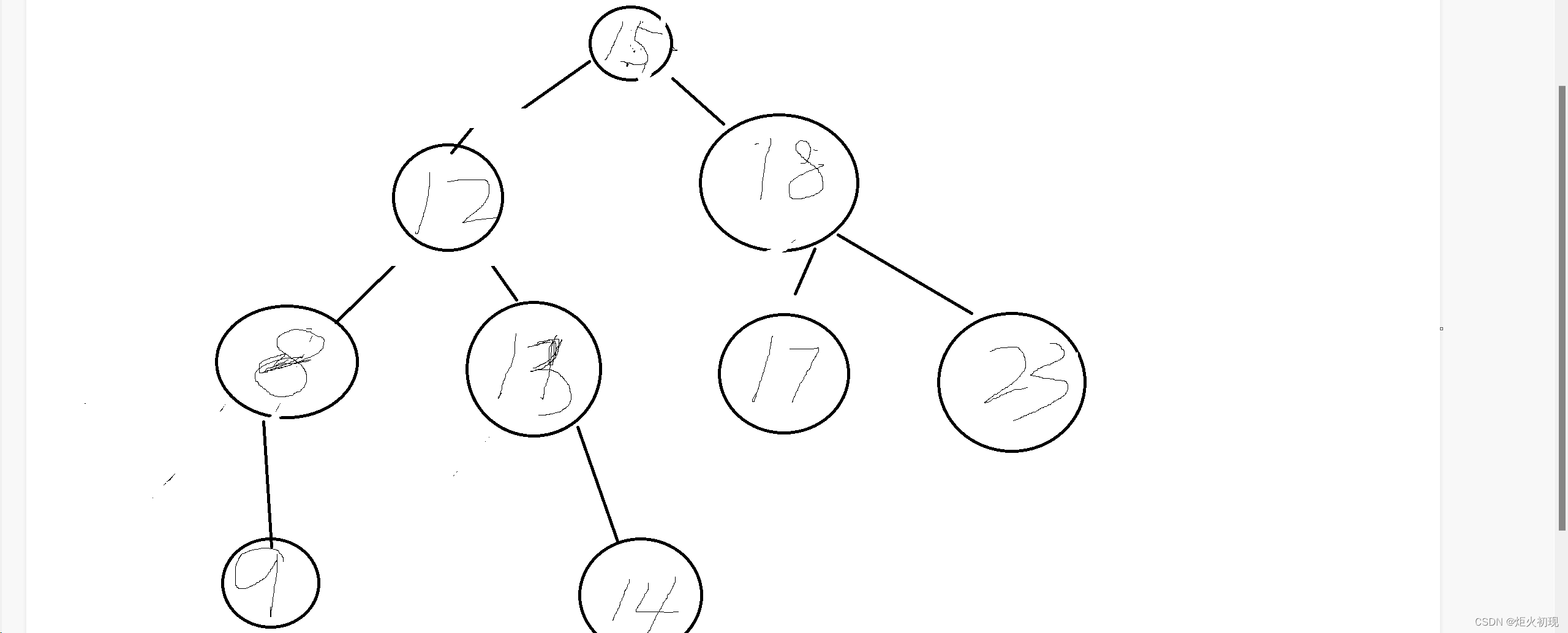
那么接下来我们就要用新的方法-----替换法

简单来说就是用10的右子树的最左节点（最小的那个）

或者左子树最右的那个节点。

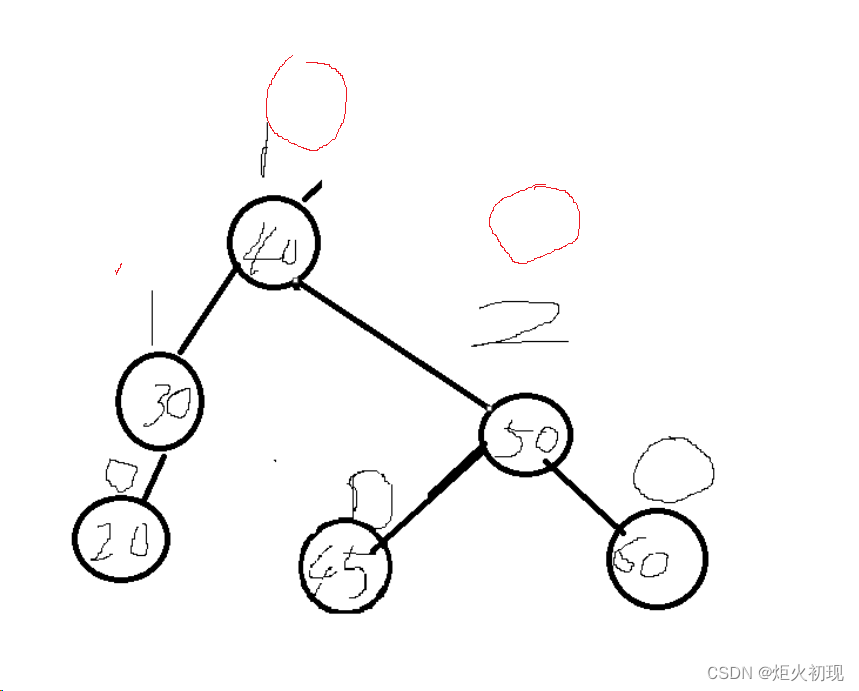
比如我们用12替换10

这个时候不仅让10消失了，而且还让树维持了平衡。

用9换10同样可以。

接下来我们就代码实现替换法。（右子树版）

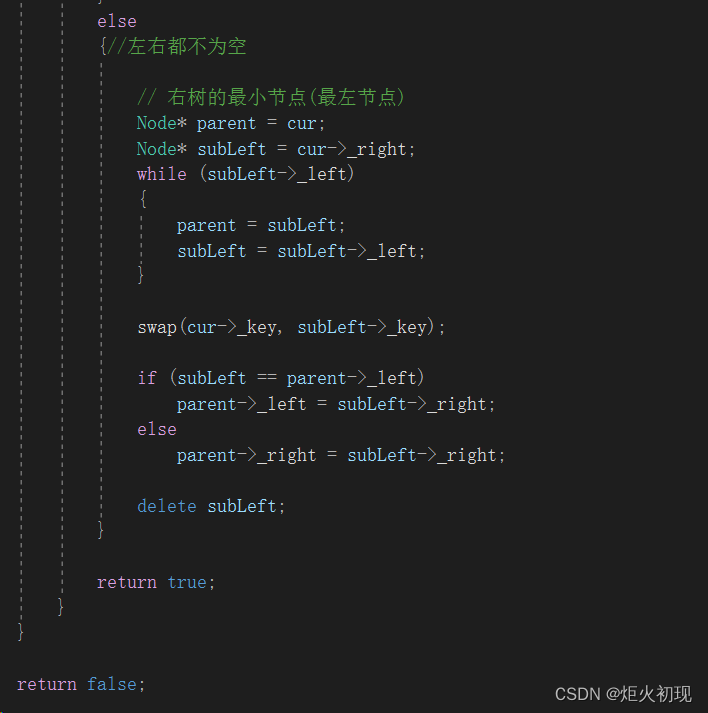
首先subleft以删除节点的右子树为根节点开始向最左子树出发。

然后替换值，并且重新进行连接。这个地方我们要注意，因为最左节点可能还有右子树，那么这个时候我们可以先记录父节点，方便进行重新连接，如果右子树只有一个节点，这个时候subleft将会是parent的右节点，除此之外都会是左节点。

然后如果不是一个节点的时候那么就相当于把父节点的左节点替换成了原本左节点的右节点

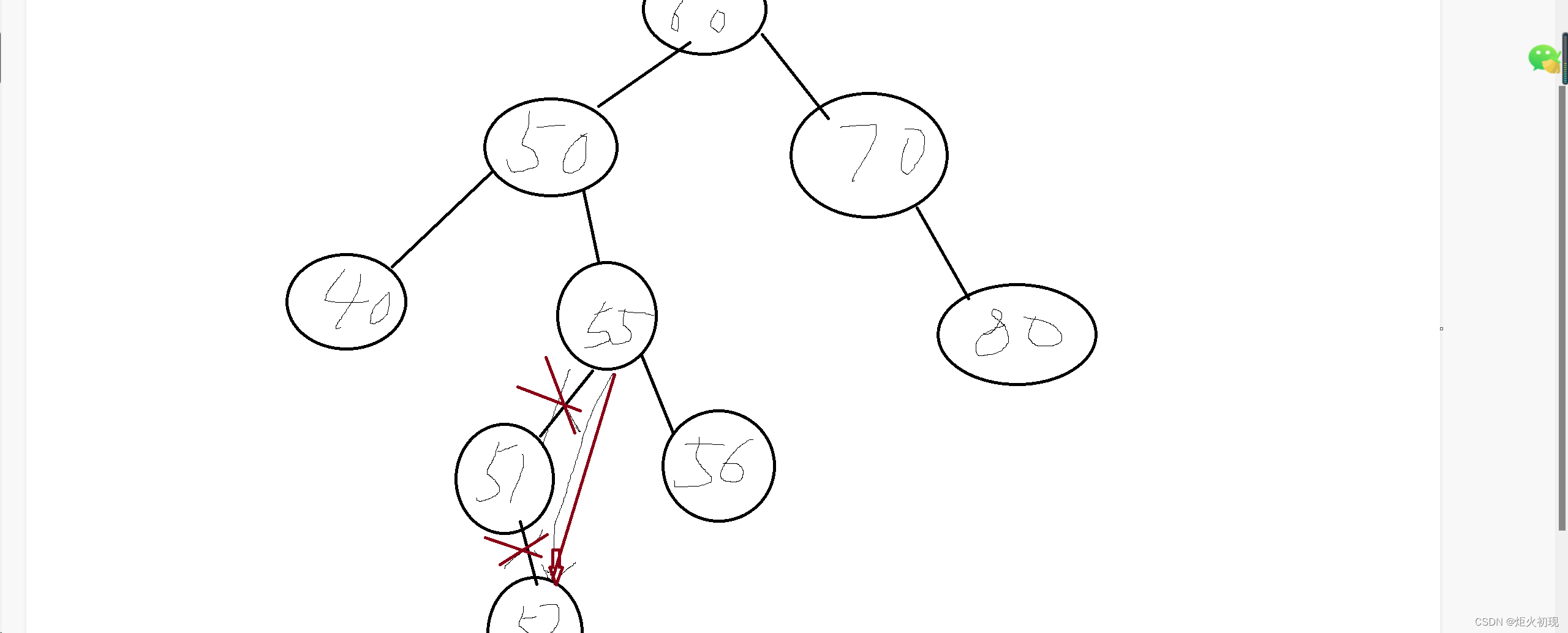
比如此处就可以将50替换成51，然后将52替换成55的左节点

如果只有一个节点相当于将50替换成55，右节点直接置空。

以上就是删除的全过程，可以多理几遍。

然后就是直接销毁（后序遍历销毁），搭配析构函数使用

接下来是构造函数的实现

首先是无参构造，没有实际内容，c++11中新增关键字dafalut（表示什么都没有）就可以在这里使用。

然后是拷贝构造，利用copy函数实现

接下来就是coy函数的实现，通过遍历进行一对一复制即可

主要就是复制一个相同的节点出来就行了。

最后就是遍历，平衡二叉树的中序遍历是升序的（性质），那么基本的平衡二叉树就讲完了。

上面讲的主要是value模型，也就是直接存储值的，接下来我们补充一下另外一种模型，叫做kv模型

也就是key-value的模型。

主要就是把数据类型更改了，基本思想没有什么改变。

接下来我们就开始讲AVL树。

我们在讲AVL树之前先要知道为什么要创造AVL树，AVL树有什么作用.

我们看下面这幅图。

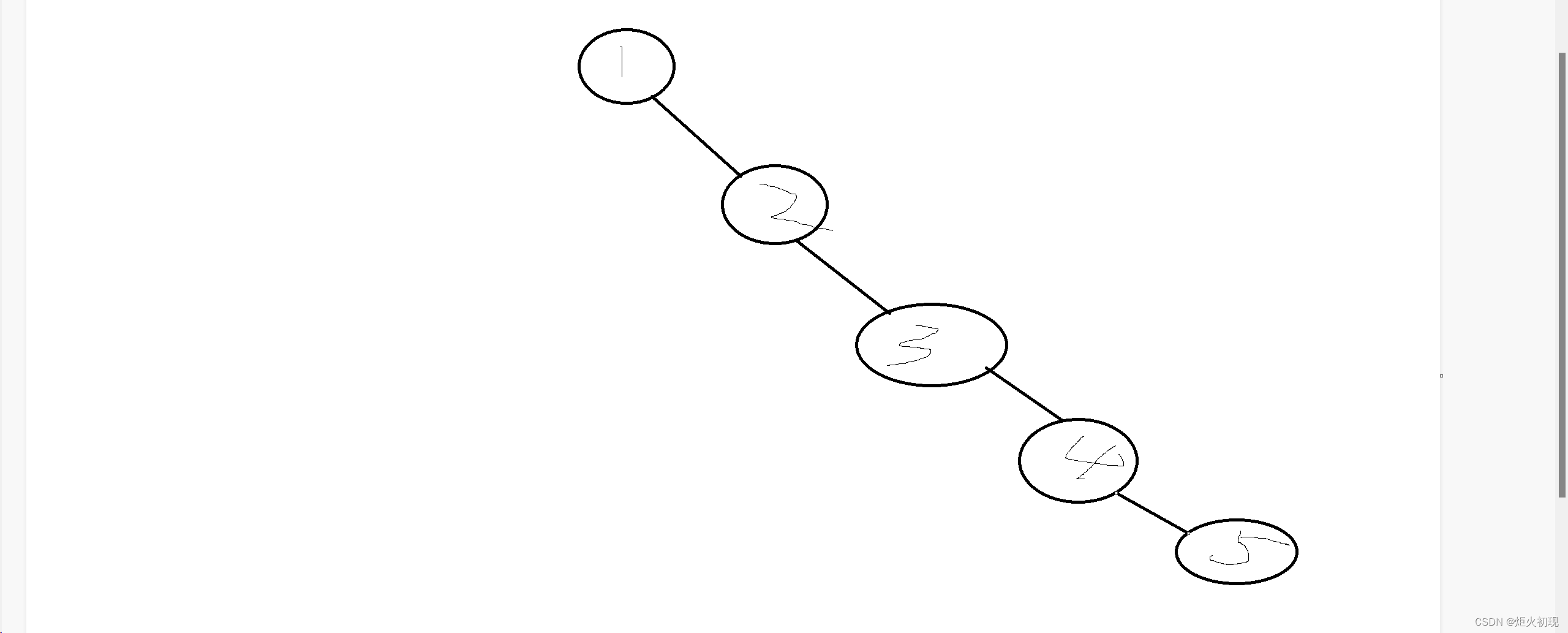
这也是一颗平衡二叉树，但是我们查找的效率却是n（时间复杂度看最坏情况）

那就是因为数据的不平衡导致的（数据都倾向于一边）

那么就违反了我们的初衷。

这个时候我们就要想办法将二叉树重新平衡，由此诞生了AVL树。

首先我们看AVL树的规则

那么我们就要来研究如何维持该规则。

比如下图就是一个违反规则的情况，那么我们必须调整去保证规则

首先我们可以引入平衡因子（可以不引入，但是比较麻烦），即右子树减去左子树的值

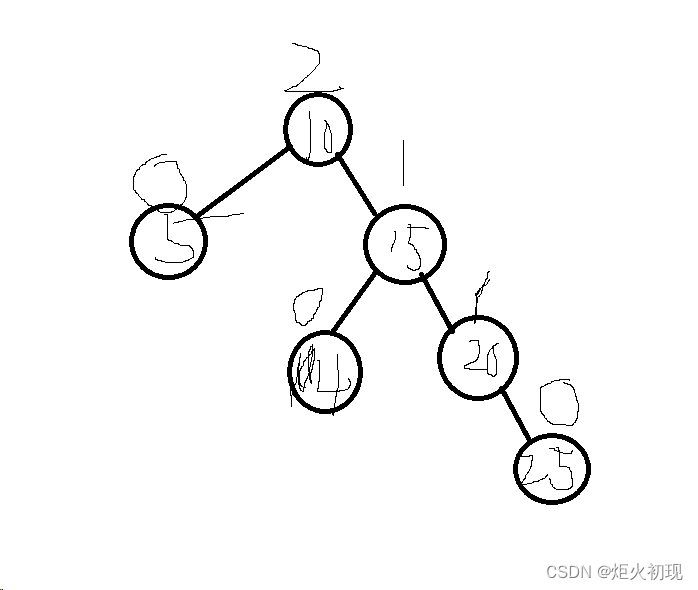
左右子树的高度差已经到达了2（+2，-2都要调整，调整方式不同），所以这个时候就必须调整了。

那么AVL树的解决方法就是旋转。

比如上图经过左旋就变成上图。

这样就符合了AVL树的定义。

总结就是

以下这种情况就要左旋

下面则是右旋的操作。

总结也就是下面这种情况要右旋

其中左旋就是将要旋转的父节点的右节点的左子树交给父节点，然后将父节点变成右节点的左子树。

右旋同理。

AVL树插入共有4种情况，上面是其中的2种。

接下来我们来介绍另外两种情况。

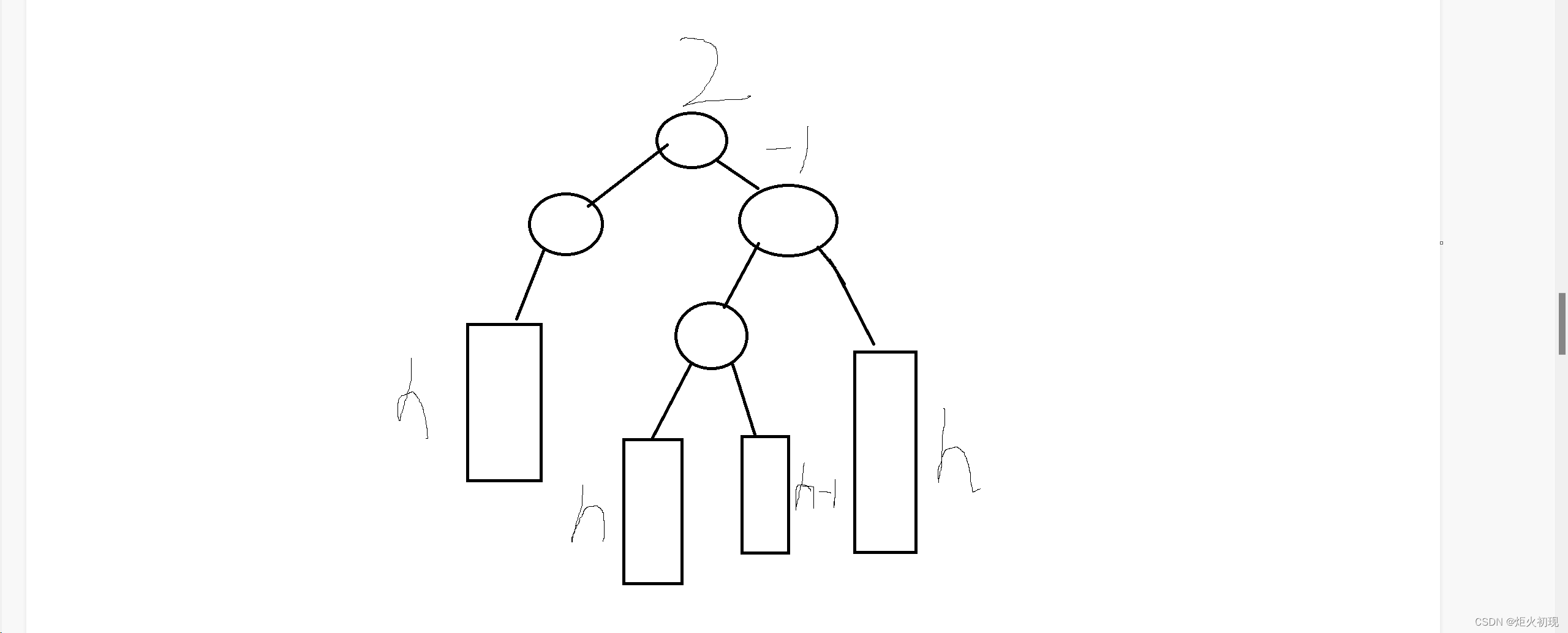
上面这个图显然无法通过左/右单旋进行修复。

那么我们可以用双旋进行恢复，如下图。

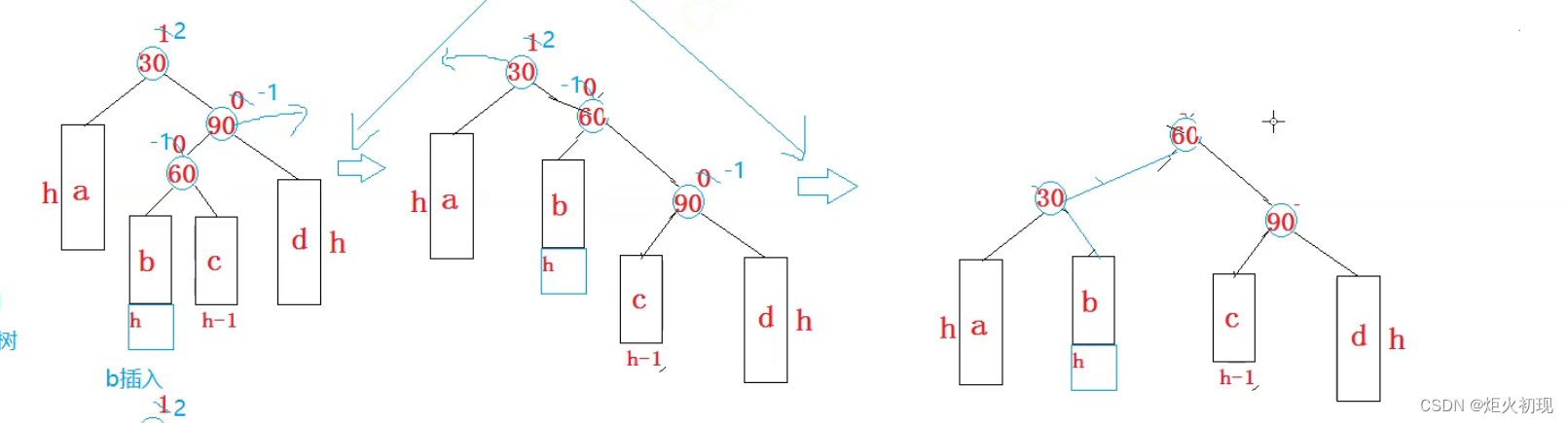
通过两次旋转就重新恢复了平衡。

插入b,c旋转方法是一致的。

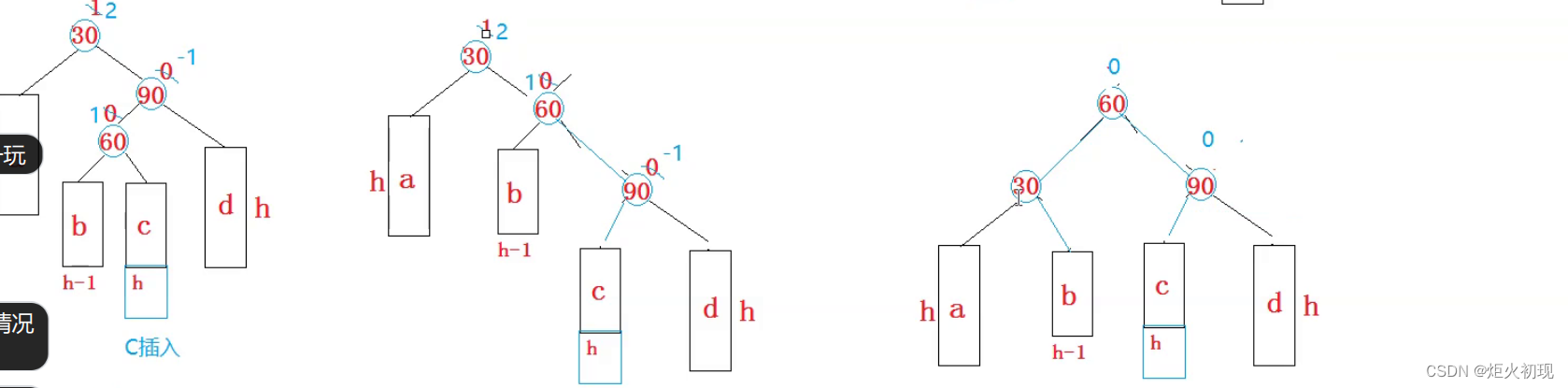
但是如果是下面这种情况则要先左旋再右旋。

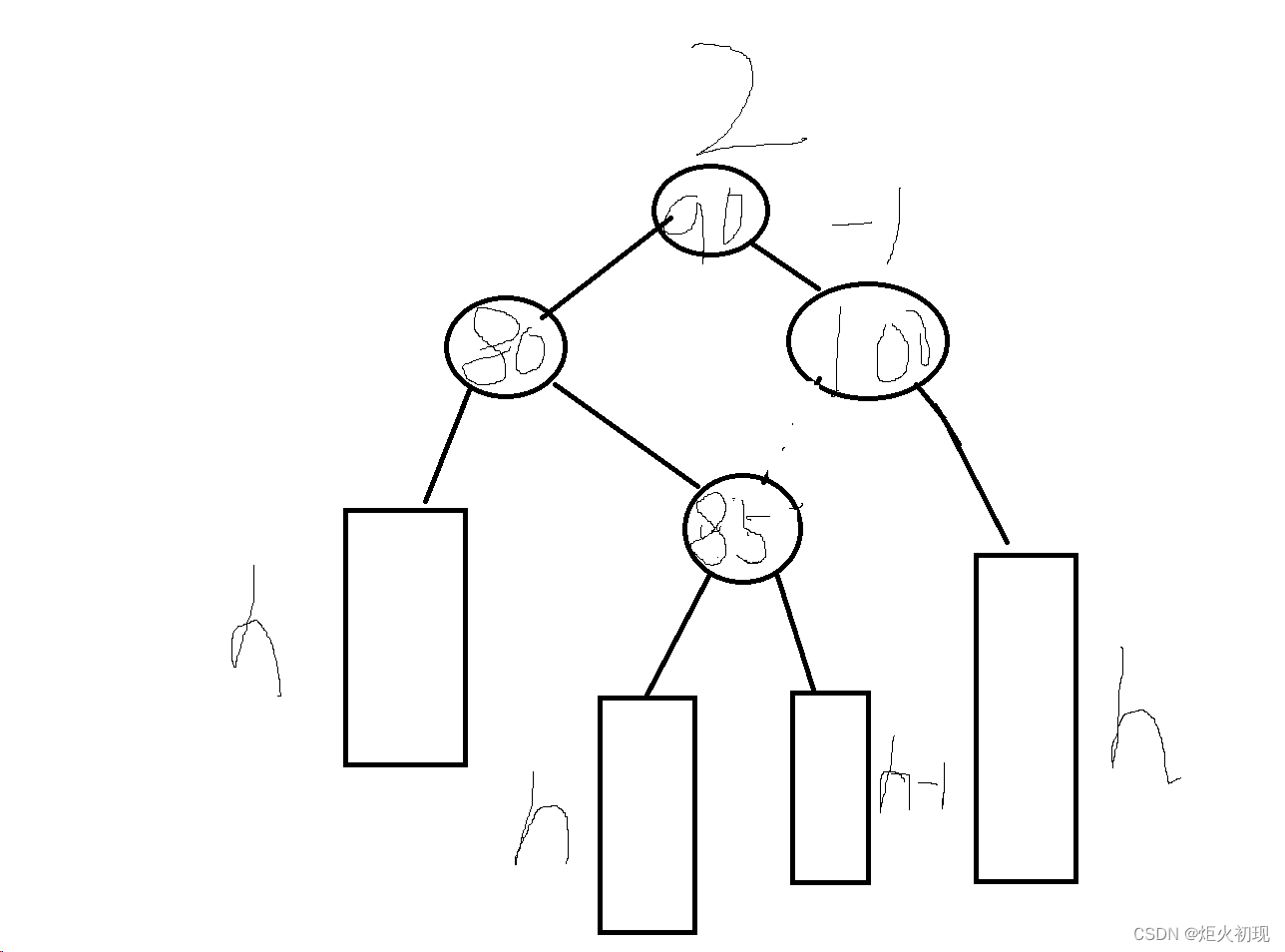
综上就是旋转的四种情况，接下来我们就要代码实现了。

首先是节点的结构，不再赘述。

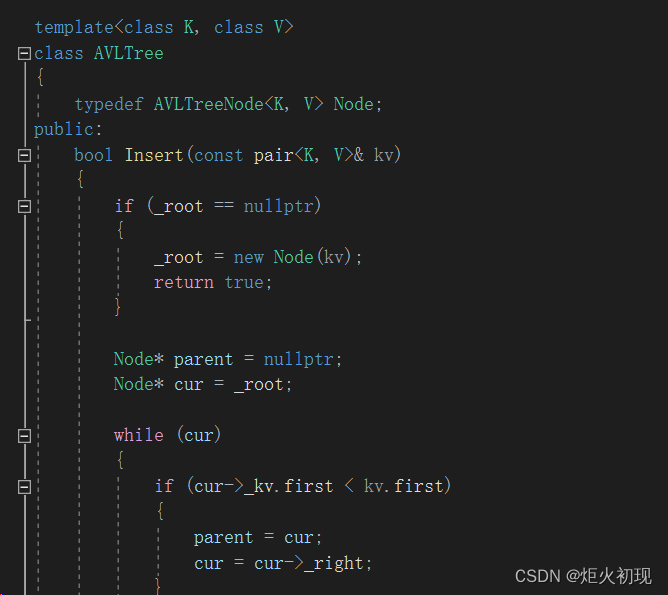
然后就是研究插入。

首先还是判断根节点的特殊情况，然后开始寻找正确的位置插入，与平衡二叉树一样。

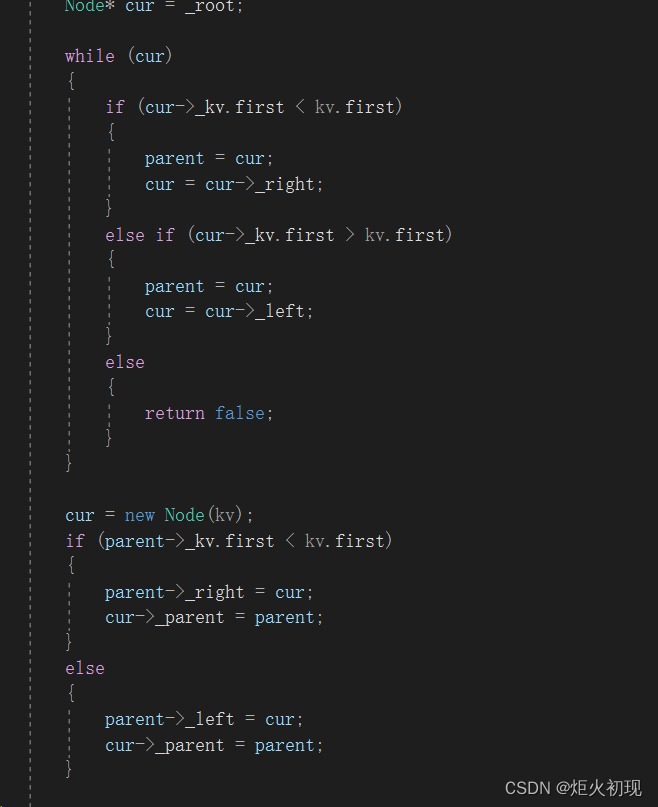
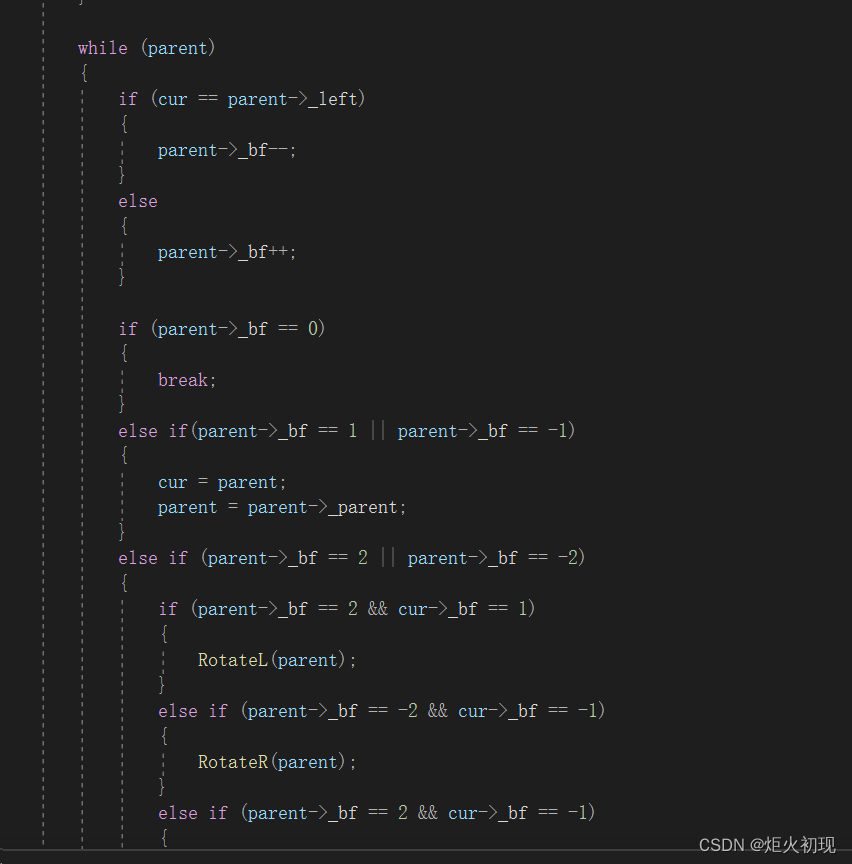
然后就是根据平衡因子判断要旋转的情况，然后进行旋转。

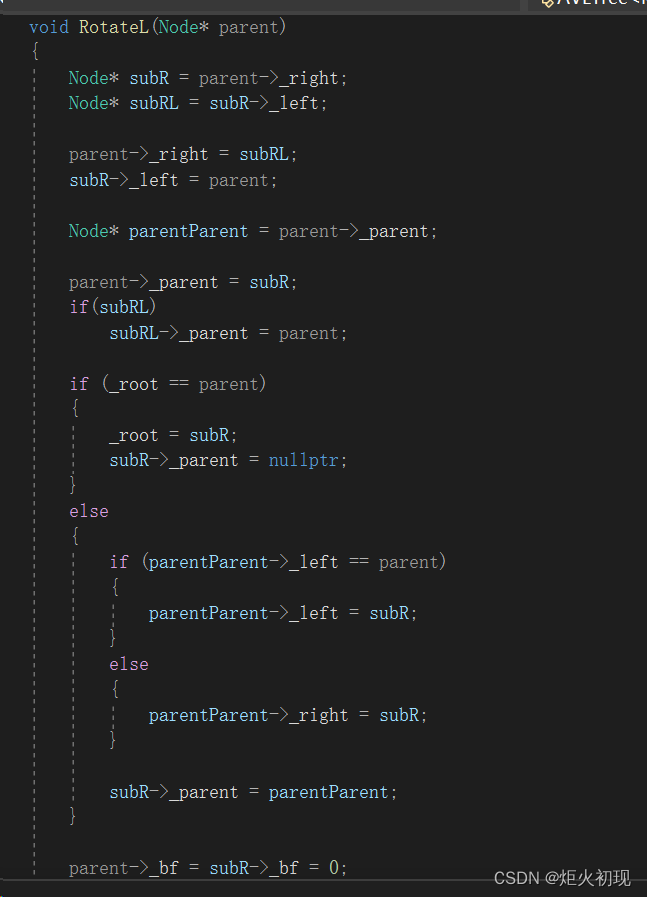
接下来是具体的旋转代码。

主要注意几点，第一由于父节点（除了根节点）都有父节点，所以为了正确连接，我们必须把它记录下来。

第二如果父亲是根节点则直接移交根节点，并且避免错误连接。

第三这个顺序一定要正确，必须提前判断根节点，否则parentParen->可能会报空。

由于本文章仅仅是了解AVL树和红黑树，就不深入探究AVL树和红黑树的删除了。

接下来我们来了解红黑树。

以下是它的规则。

此处注意这个地方的叶子不是我们平时说的叶子，而是最后的空节点。

通过上面的规则我们就可以保证最长路径不超过最短路径的2倍。（仍然是近似平衡，查找效率任然是logN）

首先还是写出节点的结构。（颜色可以使用枚举）

然后我们来思考如何维持红黑树。

主要分以下几种情况。

由于要尽量使得影响较小，插入新的节点都是红色节点。

第一种如果父节点是黑色，则符合规则，不用改动。

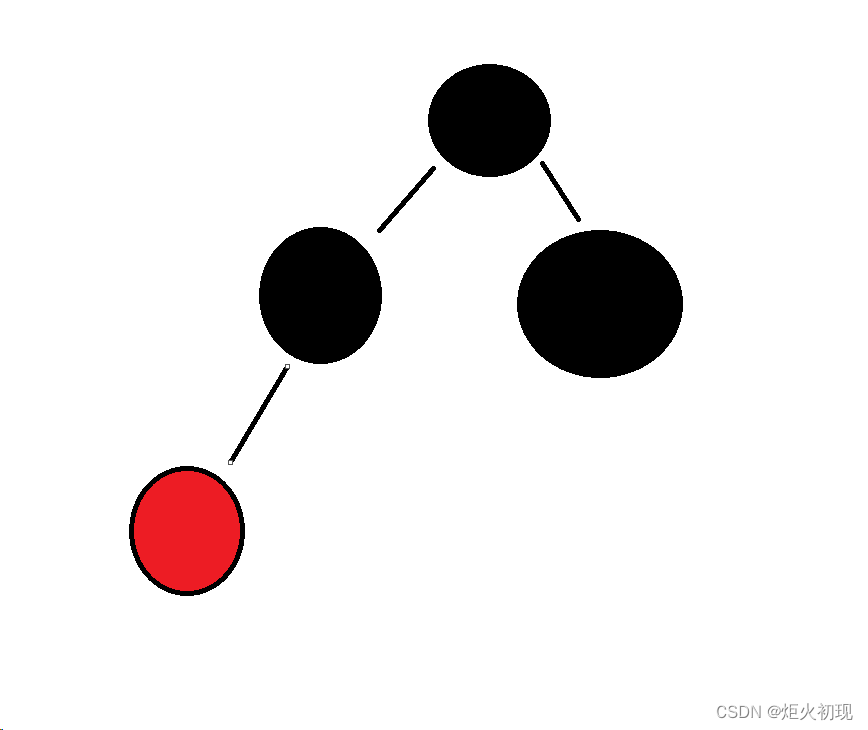
第二种，如果父节点和叔叔节点都是红色

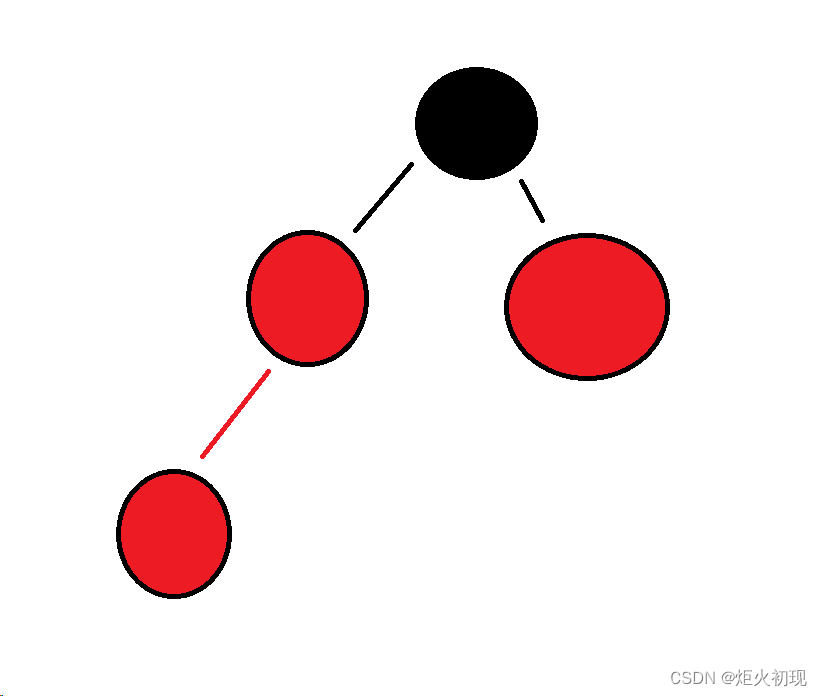
则向上更新使得父叔节点都变为黑色，祖父节点变成红色，再以祖父节点为新的开始重复此过程。

直到更新结束，最后再让根节点变为黑色即可。

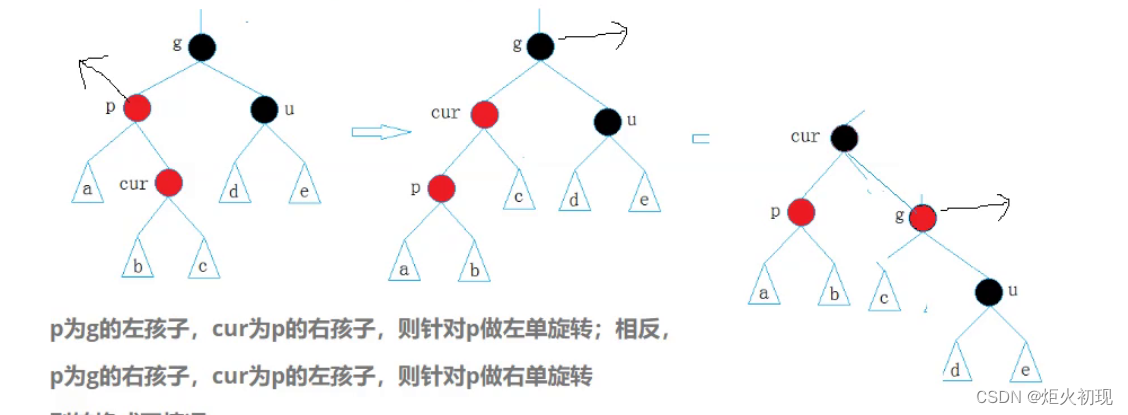
第三种则是父节点为红，叔节点为黑或者不存在。

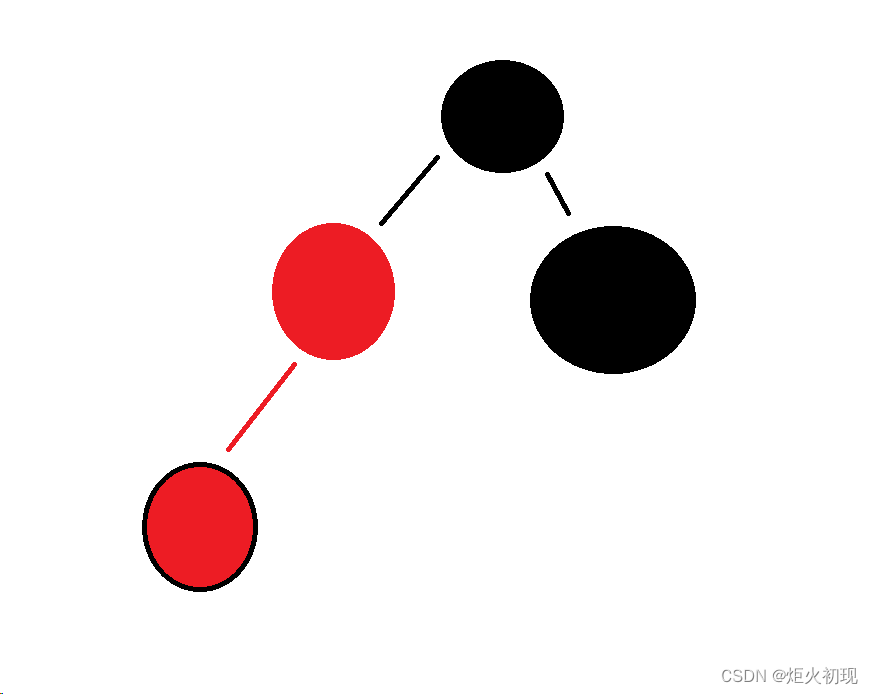
则进行旋转加变色。

接下来就是代码实现（其中包含封装，我们稍后讲解）

仍然是先判断根节点再向下寻找正确的位置。

然后开始插入新的节点。

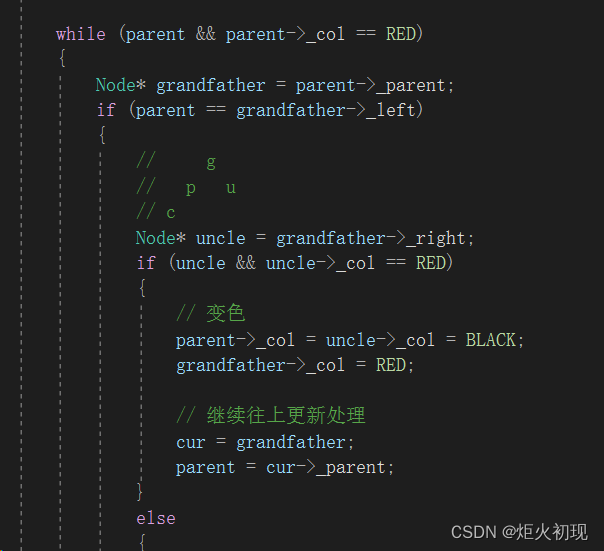
首先就是直接变色的情况，保证向上处理即可。

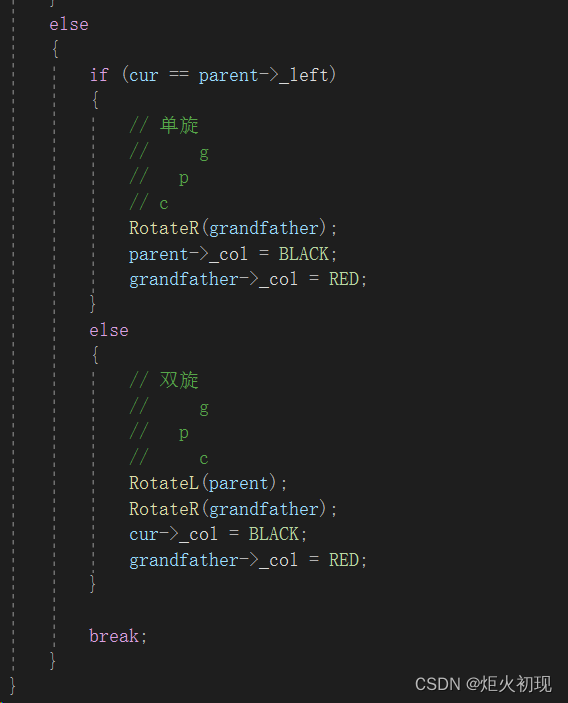
然后就是旋转的情况，先分成祖父节点的左子树和右子树，分为单旋和双旋（看插入节点是父节点的左还是右），最终都是将cur放到祖父节点，然后保持更改颜色即可。

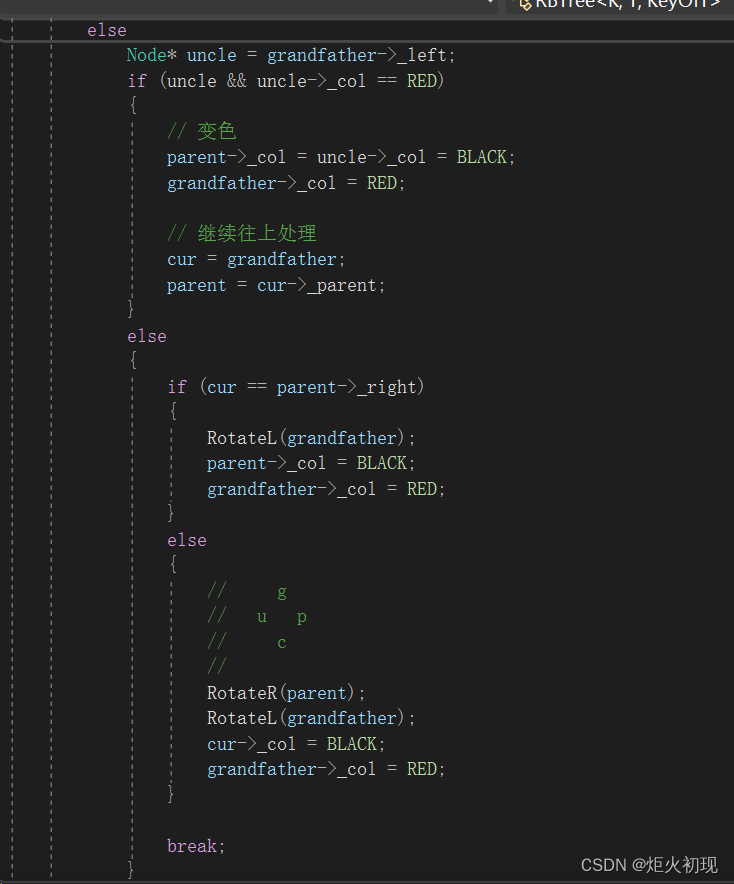
两种情况类似，不多赘述。

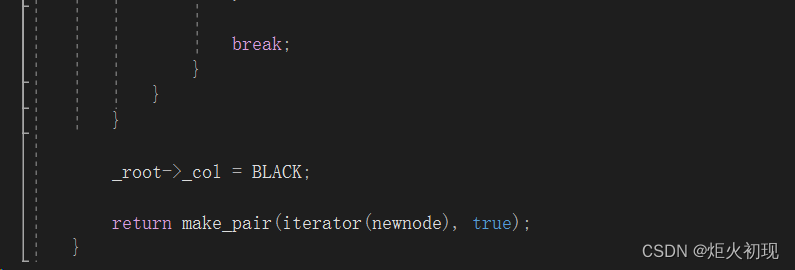
最关键的是记得保证根节点为黑色！

接下来我们来讲map和set的封装。（其底层都是红黑树）

要想封装好，首先要写好迭代器。

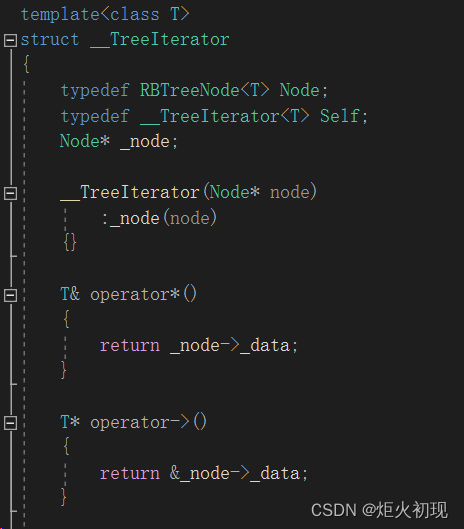
将常用的运算符重载，尤其值得注意的就是++和--（这里只讲++）

关键点是：每次查找到了右子树最后一个节点就向上找第一个孩子是父亲左的祖先，如该图6遍历完以后就去遍历8.（中序遍历）。其余的比较简单不多赘述。

接下来我们着重讲一下封装。

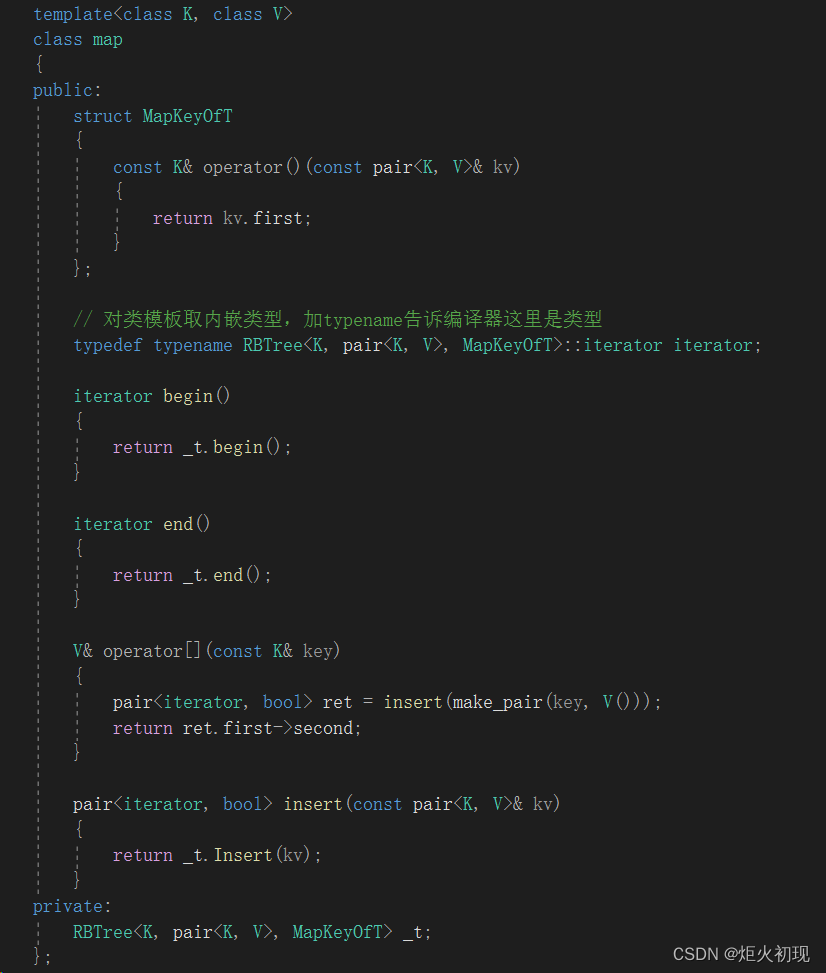
首先我们要值得map和set的不同点，前者为key-value数据，后者为key数据。

所以针对这个我们就要进行部分地方的特殊处理（其余大多数地方都可以复用）。

二者虽然是同一颗树但是通过模板的数据类型不同就可以实现存储不同的数据。

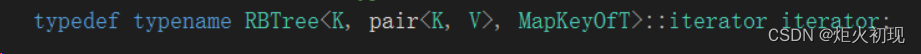
其次就是对迭代器要更改。

这样就把数据类型替换了，所以我们代码里面的比较部分就需要更改了。

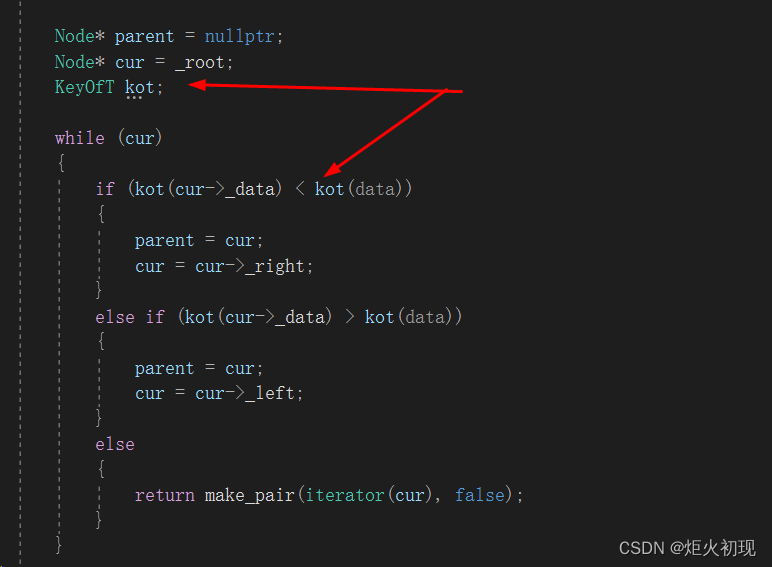
我们并没有直接调用数据，而是把数据传入我们的内部仿函数（结构体也可以当作类看待）

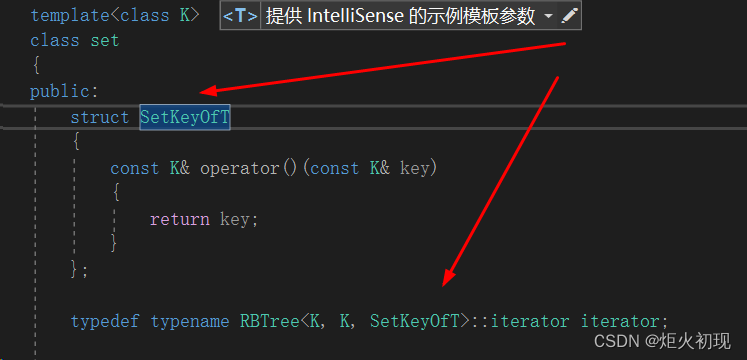
这样就实现同一棵树不同数据类型，不同数据类型不同处理方法的封装！（主要是充分复用了代码）！

 

这里要注意，由于我们要取mapkeyoft中的内嵌类型，我们不能用class，只能用typename。

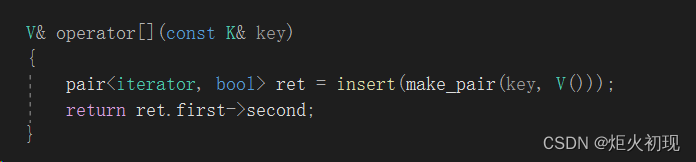
然后我们写一下insert，这个也只是通过更改传入的数据类型，复用了树本身的insert。

其中又因为insert返回的pair中有迭代器，所以重载[]的时候就可以复用Insert.

综上，就是本文的全部内容，感谢观看！