笔记：二分查找算法 | 数据结构与算法 系列教程（笔记）

题目描述

请对一个 有序数组 进行二分查找 {1,8, 10, 89, 1000, 1234}，输入一个数看看该数组是否存在此数，并且求出下 标，如果没有就提示「没有这个数」。

思路

（1)左边索引  left 为 0 ，  右边索引 right 为 数组长度 - 1；

  (2)  当left 和 right可能变化时，中间值始终为，middle = (left + right) / 2

（3）循环条件：while(left <=  ritgh) , 数组索范围。

 (4)   如果arr[中间值]  > 目标值 ，那么在左边可能有答案，此时，最右边的值 = 中间值 - 1；

（5）如果arr[中间值] < 目标值 ，那么在右边可能有答案，此时，最左边的值 = 中间值 + 1；

（6）（最后找到中间值就是答案） 

图解

实现

解法（1）——初始版

package com.ma.test;
public class BinarySearch1 {
    public static void main(String[] args) {
        int [] arr = {50,89,505,10052};
        System.out.println(binarySearchBasic(arr,50));
    }
    public static int binarySearchBasic(int[] arr, int target) {
        int left = 0;  //  设定左边的索引
        int right = arr.length - 1; // 设定右边的索引范围
        while (left <= right) {  // 索引的范围
            int middle = (left + right) / 2;
            if (arr[middle] > target) { // 中间值 > 目标值 ，说明在中间值的左边
                right = middle - 1;  // 右边值的范围 = 中间值 - 1
            } else if (arr[middle] < target) { // 中间值 < 目标值，说明在中间值的右边
                left = middle + 1;   //  左边值的范围 = 中间值 + 1
            } else {
                return middle;
            }
        }
        return -1;
    }
}

解法（2）——改动版

    public static int getValue(int arr[], int target) {
        int left = 0;
        int right = arr.length;

        while (left < right) {
            int middle = (left + right) >>> 1;
            if (target < arr[middle]) {     // 目标值  >  中间值
                right = middle;
            } else if (arr[middle] < target) {
                left = middle + 1;
            } else {
                return middle;
            }
        }
        return -1;
    }

解法（3）——二分查找（平衡板）

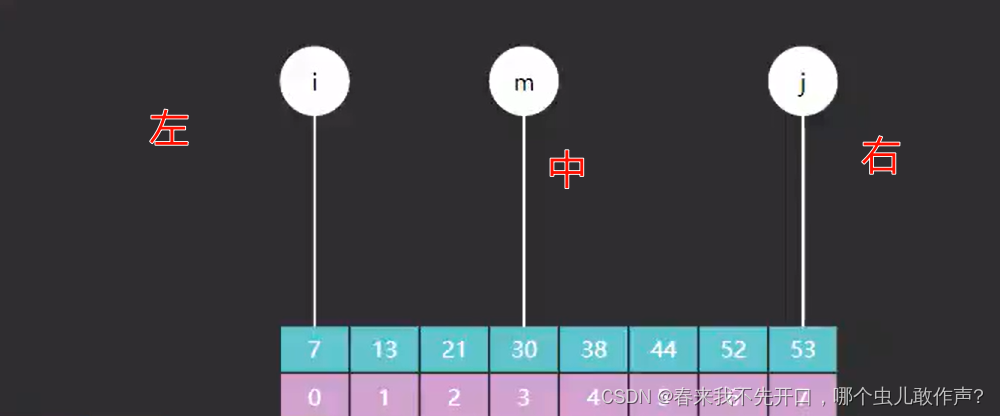
    public static int binarySearch(int[] a, int target) {
        int i = 0, j = a.length;
        while (1 < j - i) {
            int m = (i + j) >>> 1;
            if (target < a[m]) {
                j = m;
            } else {
                i = m;
            }
        }
        if (a[i] == target) {
            return i;
        } else {
            return -1;
        }
    }

 分析：

这是一个二分查找的实现，目的是在有序数组 a 中查找目标值 target。下面对代码进行逐步分析：

1. int i = 0, j = a.length;：初始化两个指针，i 表示搜索范围的起始位置，j 表示搜索范围的结束位置。一开始，搜索范围为整个数组。

2. while (1 < j - i)：使用二分查找，进入循环，条件是搜索范围的长度大于 1。这是因为当搜索范围只有一个元素时，就已经找到了目标或确定目标不在数组中。

3. int m = (i + j) >>> 1;：计算中间位置 m，使用无符号右移操作符 >>> 来防止溢出。

4. if (target < a[m]) { j = m; } else { i = m; }：根据目标值与中间值的大小关系，缩小搜索范围。如果目标值小于中间值，则在左半边搜索；否则，在右半边搜索。

5. 循环结束后，搜索范围缩小到一个元素，此时 i 就是目标值在数组中的位置。

6. if (a[i] == target) { return i; } else { return -1; }：最后检查 a[i] 是否等于目标值，如果相等，返回 i；否则，返回 -1 表示未找到目标值。

这段代码实现了二分查找算法，时间复杂度为 O(log n)，其中 n 是数组的长度。值得注意的是，这里的实现返回的是目标值在数组中的索引，如果目标值可能重复出现，这个函数只返回其中一个索引。

解法（4）——二分查找（解决值重复问题，最左边）

    public static int binarySearchBasic(int[] arr, int target) {
        int left = 0;  //  设定左边的索引
        int right = arr.length - 1; // 设定右边的索引范围
        int candidate = -1;
        while (left <= right) {  // 索引的范围
            int middle = (left + right) / 2;
            if (arr[middle] > target) { // 中间值 > 目标值 ，说明在中间值的左边
                right = middle - 1;  // 右边值的范围 = 中间值 - 1
            } else if (arr[middle] < target) { // 中间值 < 目标值，说明在中间值的右边
                left = middle + 1;   //  左边值的范围 = 中间值 + 1
            } else {
                candidate = middle;
                right = middle - 1;
            }
        }
        return candidate;
    }

 解法（5）——二分查找（解决值重复问题，最右边）

    public static int binarySearchBasic(int[] arr, int target) {
        int left = 0;  //  设定左边的索引
        int right = arr.length - 1; // 设定右边的索引范围
        int candidate = -1;
        while (left <= right) {  // 索引的范围
            int middle = (left + right) / 2;
            if (arr[middle] > target) { // 中间值 > 目标值 ，说明在中间值的左边
                right = middle - 1;  // 右边值的范围 = 中间值 - 1
            } else if (arr[middle] < target) { // 中间值 < 目标值，说明在中间值的右边
                left = middle + 1;   //  左边值的范围 = 中间值 + 1
            } else {
                candidate = middle;
                left = middle + 1;
            }
        }
        return candidate;
    }

  解法（6）——二分查找（大于目标值的 最靠左的值。）

    public static int binarySearchBasic(int[] arr, int target) {

        // left : 大于目标值的 最靠左的值。
        int left = 0;  //  设定左边的索引
        int right = arr.length - 1; // 设定右边的索引范围
        while (left <= right) {  // 索引的范围
            int middle = (left + right) / 2;
            if (target <= arr[middle]) { // 中间值 > 目标值 ，说明在中间值的左边
                right = middle - 1;  // 右边值的范围 = 中间值 - 1
            } else { // 中间值 < 目标值，说明在中间值的右边
                left = middle + 1;   //  左边值的范围 = 中间值 + 1
            }
        }
        return left;
    }

解法（7）——二分查找（目标值的最靠左元素）

    public static int binarySearchBasic(int[] arr, int target) {

        // left : 大于目标值的 最靠左的值。
        int left = 0;  //  设定左边的索引
        int right = arr.length - 1; // 设定右边的索引范围
        while (left <= right) {  // 索引的范围
            int middle = (left + right) >>> 1;
            if (target <= arr[middle]) { // 中间值 > 目标值 ，说明在中间值的左边
                right = middle - 1;  // 右边值的范围 = 中间值 - 1
            } else { // 中间值 < 目标值，说明在中间值的右边
                left = middle + 1;   //  左边值的范围 = 中间值 + 1
            }
        }
        return left - 1;
    }

产生的问题

1.    /  & <<< 的区别？

        int a = 2;
        int b = Integer.MAX_VALUE-1;

        System.out.println((a+b) / 2);
        System.out.println((a+b) >>> 1);


输出：-1073741824
      1073741824

2. 为什么结果可能不一致？

结果不一致的原因在于右移运算符和除法运算符对负数的处理方式不同。在 Java 中，右移运算符会用0填充左边空出的位，而除法运算符会根据数学规则产生截断效应。

考虑以下情况：

• a 是正整数，b 是一个接近 Integer.MAX_VALUE 的整数。在 (a + b) 中，结果可能接近 Integer.MAX_VALUE。
• 在 (a + b) / 2 中，除法运算符会将结果截断为整数，丢失了部分信息。
• 在 (a + b) >>> 1 中，无符号右移运算符则会在右边用0填充，不会截断，结果更接近原值。

因此，当 (a + b) 很大并且接近 Integer.MAX_VALUE 时，这两种方式的结果可能不一致。

衡量算法的好坏

时间复杂度

定义：时间复杂度是用来衡量：一个算法的执行，随着数据规模增大，而增长的时间成本。

说明：

* 假设算法要处理的数据规模是n，代码总的执行行数用函数f(n)来表示，例如：

   线性查找算法的函数f(n) = 3 * n + 3

   二分查找算法的函数f(n) = (floor(log2(n)) + 1) * 5 + 4

为了对f(n)进行化简，应当抓住主要矛盾，找到一个变化趋势与相近的表示法。