一、题目描述

二、思路分析

1、状态转移方程

（1）状态表示——状态压缩

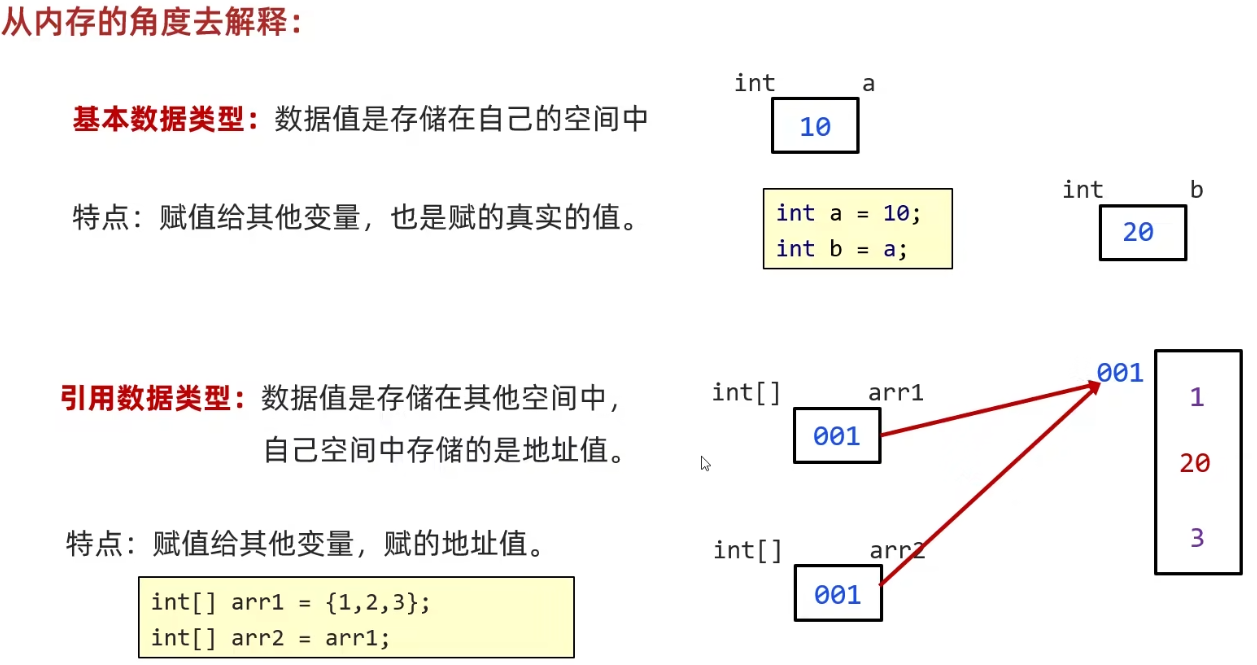
这道题的的规模大小取决于图中的点数，所以我们状态表示中肯定有一个变量表示的是当前到达的点$j$。但是，我们还需要知道，到达点$j$的时候，经过了哪些点，这样做的目的是，防止漏掉一个点或者是重复走了某个点。

我们可以把每个点是否走过用0和1表示，如果走过就是1，没走过就是0，然后这些01组成一个二进制数，然后这个二进制数的十进位表示作为我们状态转移的第二个参数$i$。

状态$i$的二进制表示中，第0位表示0号点是否走过，第1位表示1号点是否走过，依次类推。

所以：
$f(i,j)$表示到达点$j$的时候，经过了数字$i$所表达的状态中的点，所需要的最短路程。

（2）状态转移

$$f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j])$$

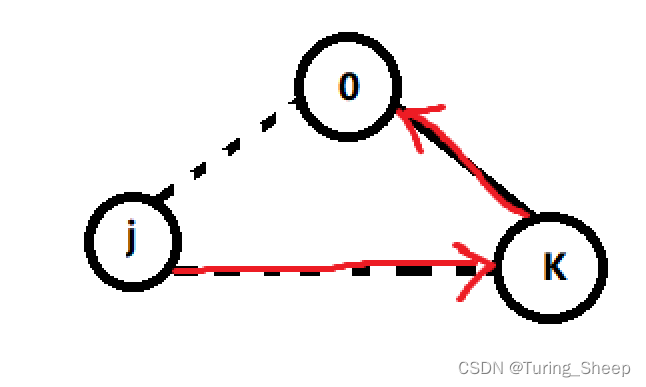
转移方程中的：$i-(1<<j)$是为了保证不重复经过$j$。

2、循环和初始化

（1）循环设计

根据我们的转移方程，我们发现，我们遇到的子问题是状态$[i-(1<<j)]$。

也就是说我们需要提前算出这个状态下的值。

所以外循环是我们经过的点的状态$i$，内层是$j$。

如果我们反过来外层枚举$j$，内层枚举状态$i$。那么当我们的$k$大于j的时候，此时的状态是没有被算出来的。所以这种枚举顺序是错误的。

（2）初始化

为了最小值，我们会将数组全初始化为正无穷。但是我们需要知道最小子问题的答案。那最小的子问题其实就是0号点到自身的路程，这个路程是0。
同时，由于经过了0号点，所以二进制的0号位是1，其余位置是0。
即$f[1][0]=0$

三、代码实现

#include<iostream>
#include<cstring>
using namespace std;
const int N=21,M=1<<N;
int f[M][N],g[N][N];
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            cin>>g[i][j];
    
    memset(f,0x3f,sizeof f);
    f[1][0]=0;
    for(int i=0;i<1<<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            if(i>>j&1)
            {
                for(int k=0;k<n;k++)
                {
                    if((i-(1<<j))>>k&1)
                    {
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+g[k][j]);
                    }
                }
            }
        }
    }
    cout<<f[(1<<n)-1][n-1]<<endl;
    return 0;
}