在处理数据过程中，通常会有不同规格的数据，比如年龄的取值范围是0-130，收入的取值范围是0-100000等等，如果不进行归一化或标准化处理，梯度下降每次走过的相对长度就不一样，就导致某个参数很快就找到了最优解，另一个参数还早得很。

归一化（Normalization）

归一化是将数据缩放到固定范围内的过程，最常见的是0到1之间。这种方法尤其适用于参数的尺度相差很大的情况。归一化的原理就是整体缩放数据刀0-1之间，公式是：

$$x_{\text{normalized}}=\frac{x-x_{\text{min}}}{x_{\text{max}}-x_{\text{min}}}$$

其中，$x$是原始数据点，$x_{\text{min}}$和$x_{\text{max}}$分别是数据集中的最小值和最大值。

归一化适用于不假设数据分布的算法，如K最近邻和神经网络。

标准化（Z-Score Standardization）

标准化涉及到数据的重新缩放，使得它们的均值为0，标准差为1。标准化就是相当于把原来正太分布的数据移动到x=0的位置，让数据中位值和y轴重叠，同时数据集中的值在其均值周围分布的平均距离是1，因为平均距离是1但是大量数据集中在1以内（即-1～1之间）因此1以外的大概会分布到-3～3之间，最终就形成大部分数据在-3～3之间。公式是：

$$x_{\text{standardized}}=\frac{x-\mu }{\sigma }$$

其中，$\mu$是数据集的均值，而$\sigma$是数据集的标准差。

标准化适用于假设数据为正态分布的算法，如线性回归和逻辑回归。

归一化和标准化的代码实现如下：

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布的特征X和目标y数据
X = np.random.normal(50, 10, 1000)
y = np.random.normal(30, 5, 1000)

# 归一化y
normalized_y = (y - np.min(y)) / (np.max(y) - np.min(y))

# 标准化y
standardized_y = (y - np.mean(y)) / np.std(y)

# 绘制散点图
plt.figure(figsize=(15, 5))

# 绘制原始数据的散点图
plt.subplot(1, 3, 1)
plt.scatter(X, y, alpha=0.6, color='blue')
plt.title('Original Data Scatter Plot')
plt.xlabel('X')
plt.ylabel('y')

# 绘制归一化后的数据散点图
plt.subplot(1, 3, 2)
plt.scatter(X, normalized_y, alpha=0.6, color='orange')
plt.title('Normalized Data Scatter Plot')
plt.xlabel('X')
plt.ylabel('Normalized y')

# 绘制标准化后的数据散点图
plt.subplot(1, 3, 3)
plt.scatter(X, standardized_y, alpha=0.6, color='green')
plt.title('Standardized Data Scatter Plot')
plt.xlabel('X')
plt.ylabel('Standardized y')

plt.tight_layout()
plt.show()

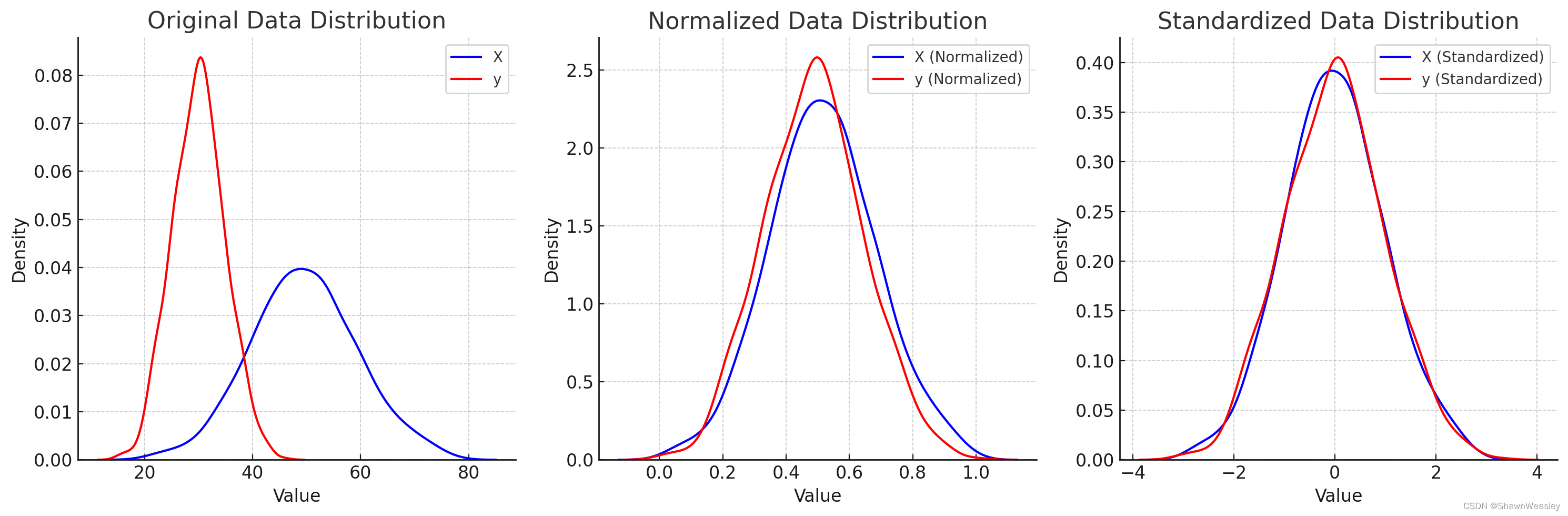
图像绘制的结果，可以看到y的取值分别进行了归一化和标准化：

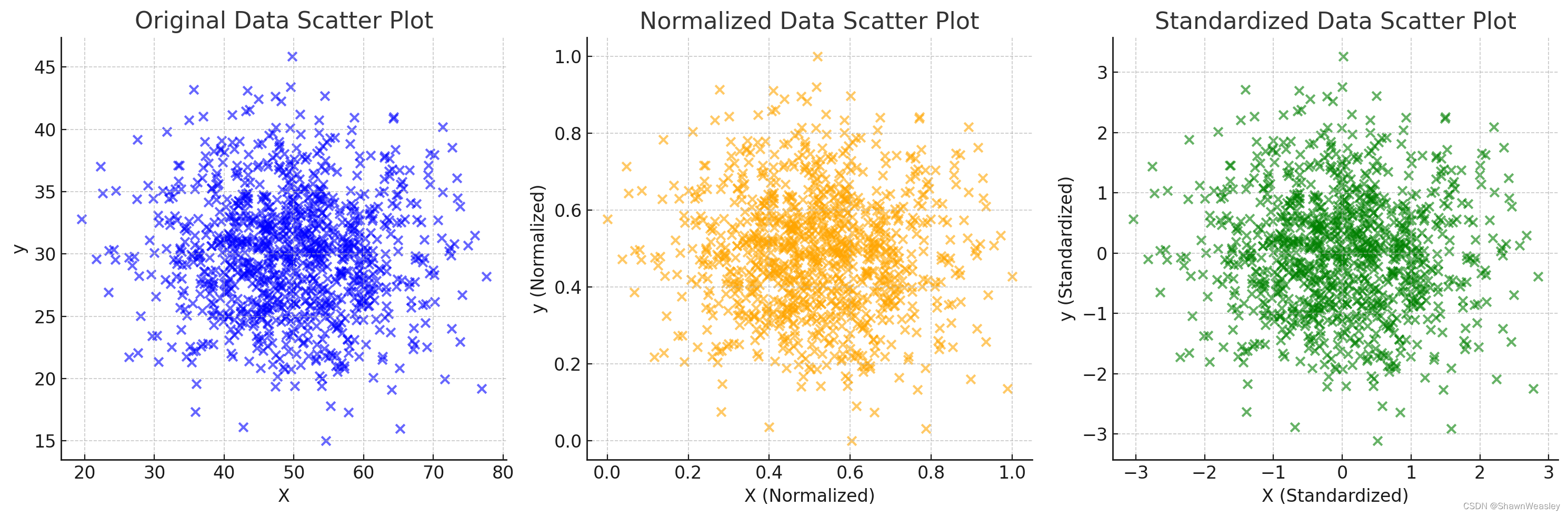
使用了Seaborn库来绘制原始数据、归一化后的数据和标准化后的数据的密度分布（KDE，Kernel Density Estimation）。这些图表显示了数据在不同处理（归一化和标准化）后的分布情况。

在第一个图表（Original Data Distribution）中，您可以看到特征$X$（蓝色）和目标 $y$（红色）的原始分布情况。
第二个图表（Normalized Data Distribution）展示了将 $X$和$y$ 归一化后的分布情况。
第三个图表（Standardized Data Distribution）则展示了$X$和$y$标准化后的分布情况。