老规矩,看目录,平均3-5题
文章目录
- A/B
- 2023
- 真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还是别感觉了;-纯蒙猜-哪个长选哪个【不要用这招,因为两个选项,总会有一个长的,那不就大多都是A/B,但其实每年平均3-5题】;
- 真题(2023-22)-A选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立;-不要强行当成“取值范围”和“包含关系”
- 真题(2023-25)-B-选项特点:两个大于号;不要强行当成“取值范围”和“包含关系”
- 2022
- 真题(2022-17)-A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 真题(2022-19)-B-选项特点:一个等号,一个特殊符号;
- 真题(2022-22)-B-选项特点:两个已知X的值;看着像可以联立,所以其实光看,是看不出是否要联立的
- 2021
- 真题(2021-20)-A-无法判断条件是否需要联立;若用“一字之差”,也无法判断那个信息不完全
- 真题(2021-22)-A-选项特点:两个已知X的值;-不要强行包含关系了-容易判断不需要联立,选A/B/D/E;
- 2020
- 真题(2020-16)-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D!!!错了
- 真题(2020-23)A-选项特点:一个大于号,一个小于号;选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D,但是错了!!!
- 真题(2020-24)-A-选项特点:两个等号;-先分析选项是否需要联合⇒不需要(这里不好判断是否需要)⇒单一型⇒选项间的关系⇒有包含关系⇒选范围小的,选B!!!错了
- 真题(2020-25)-A-选项特点:两个等号;无法判断是否需要联立;-选项是两个等式,特值法
- 2019
- 真题(2019-18)A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 真题(2019-21)-B-边长关系推面积,选B
- 真题(2019-24)-A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
- 真题(2019-25)-A-选项特点:两个等号;-先分析选项是否需要联合⇒不需要⇒单一型⇒选项间的关系⇒有包含关系,选范围小的,选A;-A-一字之差-两个条件相似程度较高,选信息量少的
- 2018
- 真题(2018-16)-A-选项特点:两个小于号;-先分析选项是否需要联合⇒不需要(看不出)⇒单一型⇒选项间的关系⇒无共边界反向范围,无包含关系⇒尝试特值法1;两个等号使用特值法;
- 真题(2018-17)-B-选项特点:两个等号-要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
- 真题(2018-24)-A-选项特点:两个大于号
- 2017
- 真题(2017-17)-A-选项特点:两个等号;
- 真题(2017-19)-B-选项特点:两个大于号;
- 真题(2017-21)-B-选项特点:两个已知X的值;要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
- 真题(2017-22)-A
- 真题(2017-25)-A-选项特点:一个小于号,一个等号;容易误判选C,因为【一个不等号,一个等号,选C】
- 2016
- 真题(2016-16)-B-要素列表法-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;-B-数据分析-平均值-加权平均值
- 真题(2016-18)-A-选项特点:两个等号;
- 真题(2016-21)-A-要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;-A-数据分析-平均值与方差-方差是有平方,解出两个根,不能确定;容易误判联立,毕竟均值和方差看着就是一起的。
- 真题(2016-23)-B-选项特点:两个等号;要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;两个等号用特值法
- 真题(2016-24)-A-要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;
- 2015
- 真题(2015-17)-A;-选项特点:两个大于等于号;
- 真题(2015-18)-B;两个等号用特值法,但是这题用不了
- 真题(2015-19)-B-选项特点:两个等号;
- 真题(2015-21)-B-两个大于号;
- 2014
- 真题(2014-16)-A
- 真题(2014-17)-选项特点:一个大于,一个小于;B-特值体系法-三、无解/恒成立型特值;-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D,但是错了!!!!!
- 真题(2014-19)-A-选项特点:两个等号;要素列表法plus-特殊套路-一次与二次-条件偶次+结论奇次⟹不充分;
- 真题(2014-20)-A-选项特点:两个已知X的值;
- 真题(2014-21)-A-容易误判C,因为【一个定量,一个定性】
- 真题(2014-25)-A-两个大于号
- 2013
- 真题(2013-16)-A-两个等号
- 真题(2013-18)-B-两个等号
- 真题(2013-19)-A-选项特点:两个等号;-特值法体系-两项特值与三项特值;-A-代数-函数-一元二次函数-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
- 真题(2013-23)-B
- 真题(2013-24)-A
选A或B选项(只有一个条件充分,另一个不充分)
考试中10道题里最多5道,一般是4道,如果两条件复杂程度有明显差异时,可以使用以下技巧快速解答。
原则1:当两条件矛盾时(占近一半)由于A和B的选项可能要远远高于E,所以大家在做题时应该选择一个比较容易的条件下手,如果能成立,再去验证另一个选项,如果不成立,另一个条件成立的可能性很大。
原则2:当两条件有包含关系时,优先选择范围小的(A、B),做题时应先选择范围较大的先做,若范围较大的条件充分,则选D,若范围较大的不充分,则小范围成立的可能性非常大。
原则3:某一个条件对题干无作用,选另一个有作用的条件为充分。
纯蒙猜
原则1:印刷的长度明显不同时,选复杂的选项(简言之,哪个长选那个)
原则2:印刷长度相当时。包含考点相对较难、公式相对复杂、方法较难、运算量大的项更充分。
原则3:两条件是数值形式,数值复杂的优先充分;表现为:负大于正;不易整除大于易整除;绝对值大于不含绝对值;含根号大于不含根号;对数函数复杂程度大于指数函数复杂程度大于幂函数复杂程度。
原则4:一个为相对量的百分比,另一个为绝对量的数值,优先选百分比。
包含性选项秒杀-准确率80%-A/B:
(1)条件2包含于条件1,选A或D,80%选A,20%选D。
(2)条件1包含于条件2,选B或D,80%选B,20%选D。
A/B型蒙猜
“条件题”:A/B型秒杀——【】
1.一字之差:即两个条件相似程度较高
例:条件(1):
a
n
=
2
n
−
1
(
n
=
1
,
2
,
.
.
.
)
a_n=2n-1(n=1,2,...)
an=2n−1(n=1,2,...);条件(2):
a
n
=
2
n
(
n
=
1
,
2
,
.
.
.
)
a_n=2n(n=1,2,...)
an=2n(n=1,2,...)
一字之差拓展:一个条件信息不完全,选另一个;即虽然一字之差,但条件信息不完成;一个信息量大,一个信息量少,选择不言而喻。
例1:题干给出结论大于0.8,选B;
条件(1):0.81;条件(2):0.9;
有形如(=某数字)的等式约束范围限制的,选数小的。
例1:题干给出
a
+
b
+
c
+
d
a+b+c+d
a+b+c+d的最大值,选B。
条件(1):
a
b
c
d
=
2700
abcd=2700
abcd=2700;条件(2):
a
d
c
d
=
2000
adcd=2000
adcd=2000。
例1:题干求
a
,
b
,
c
a,b,c
a,b,c的乘积,选A。
条件(1):
a
+
b
+
16
;
a+b+16;
a+b+16;条件(2):
a
+
b
+
c
=
20
a+b+c=20
a+b+c=20。
2.共边界反向范围型:
反向范围型:
例1:题干求范围;选A;
条件(1):
−
3
1
<
k
<
0
;
-\frac{\sqrt{3}}{1}<k<0;
−13<k<0;条件(2):
0
<
k
<
2
2
0<k<\frac{\sqrt{2}}{2}
0<k<22
3.“暗”包含型范围
⟹
\Longrightarrow
⟹ 选大的;
例:条件(1)与条件(2)是包含的;
⟹
\Longrightarrow
⟹ 选项A包含B;则选包含多的。
4.面积比+边长比:即边长关系推面积时,往往选B;
5.几何中要确定一个要素:
例:题干要确定一个要(无)X的值;即其一定与条件中的一个强相关;A or B。
【总结:
“条件题”中A/B型秒杀:
(1)每个条件单独就够用(一眼看不大可能联合)
(2)两个条件不大可能都对;
分类如下:
1.一字之差:一个条件信息不完全,选另一个;
2.共边界反向范围型;
3.面积比+边长比;
4.几何中要确定一个要素;
5.“暗”包含型范围
⟹
\Longrightarrow
⟹ 选大的;】
A/B
2023
真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还是别感觉了;-纯蒙猜-哪个长选哪个【不要用这招,因为两个选项,总会有一个长的,那不就大多都是A/B,但其实每年平均3-5题】;
-几何-解析几何-最值
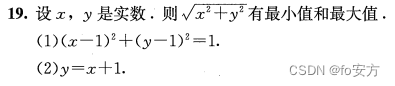

真题(2023-22)-A选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立;-不要强行当成“取值范围”和“包含关系”
-算术-质数-2,3,5,7,11,13,17,19,23,29-穷举法


真题(2023-25)-B-选项特点:两个大于号;不要强行当成“取值范围”和“包含关系”
-数据分析-概率-已知事件的概率求概率⟹ 独立事件概型⟹ 乘法计算概率


2022
真题(2022-17)-A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-算术-绝对值-绝对值号和未知数-线性和差-线性差最值:相减最大和最小,大小互减取最值,互为相反两边跑,后者居上描画好(“后者居上描画好”:是指在减号后面的绝对值的零点处取最大值,图像是楼梯的上层,由此可以描点画出图像。)
17.设实数𝑥𝑥满足
∣
x
−
2
∣
−
∣
x
−
3
∣
=
a
|x-2|-|x-3|=a
∣x−2∣−∣x−3∣=a,则能确定𝑥的值。
(1)
0
<
a
≤
1
2
0<a≤\frac{1}{2}
0<a≤21
(2)
1
2
<
a
≤
1
\frac{1}{2}<a≤1
21<a≤1

真题(2022-19)-B-选项特点:一个等号,一个特殊符号;
-数列-等比数列
19.在△ 𝐴𝐵𝐶 中,𝐷 为 𝐵𝐶 边上的点, 𝐵𝐷 、 𝐴𝐵 、 𝐵𝐶 成等比数列,则 ∠𝐵𝐴𝐶 = 90°
(1)𝐵𝐷 = 𝐷𝐶。
(2) 𝐴𝐷 ⊥ 𝐵𝐶。

真题(2022-22)-B-选项特点:两个已知X的值;看着像可以联立,所以其实光看,是看不出是否要联立的
-代数-分式-升降幂法
22.已知𝑥为正实数,则能确定𝑥−
1
x
\frac{1}{x}
x1的值
(1)已知
x
+
1
x
{\sqrt{x}}+\frac{1}{\sqrt{x}}
x+x1的值
(2)已知
x
2
−
1
x
2
x^2-\frac{1}{x^2}
x2−x21的值

2021
真题(2021-20)-A-无法判断条件是否需要联立;若用“一字之差”,也无法判断那个信息不完全
-几何-解析几何-位置-线圆位置-相切-点到直线的距离公式:
l
:
a
x
+
b
y
+
c
=
0
l:ax+by+c=0
l:ax+by+c=0,点(
x
0
,
y
0
x_0,y_0
x0,y0)到
l
l
l的距离为
d
=
∣
a
x
0
+
b
y
0
+
c
∣
a
2
+
b
2
d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}
d=a2+b2∣ax0+by0+c∣
20.设a为实数,圆C:
x
2
+
y
2
=
a
x
+
a
y
x^2+y^2=ax+ay
x2+y2=ax+ay,则能确定圆C的方程。
(1)直线
x
+
y
=
1
x +y=1
x+y=1与圆C相切。
(2)直线
x
−
y
=
1
x-y =1
x−y=1与圆C相切。

真题(2021-22)-A-选项特点:两个已知X的值;-不要强行包含关系了-容易判断不需要联立,选A/B/D/E;
-应用题-出现了两个及以上未知量,而数量关系却少于未知量的个数-不定方程-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
22.某人购买了果汁、牛奶、咖啡三种物品,已知果汁每瓶12元,牛奶每瓶15元,咖啡每盒35元,则能确定所买各种物品的数量。
(1)总花费为104元。
(2)总花费为215元。

2020
真题(2020-16)-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D!!!错了
-几何-平面几何-三角形-心
16、在△ABC 中,∠B=
6
0
0
60^0
600,则
c
/
a
>
2
c/a>2
c/a>2
(1)
∠
C
<
9
0
0
∠C<90^0
∠C<900
(2)
∠
C
>
9
0
0
∠C>90^0
∠C>900


真题(2020-23)A-选项特点:一个大于号,一个小于号;选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D,但是错了!!!
特值法体系-两项特值与三项特值;
-A-代数-方程-一元二次方程-根的分布
23、设函数
f
(
x
)
=
(
a
x
−
1
)
(
x
−
4
)
f(x)=(ax-1)(x-4)
f(x)=(ax−1)(x−4),则在 x = 4 左侧附近有
f
(
x
)
<
0
f(x)<0
f(x)<0。
(1)
a
>
1
4
a>\frac{1}{4}
a>41
(2)
a
<
4
a<4
a<4



真题(2020-24)-A-选项特点:两个等号;-先分析选项是否需要联合⇒不需要(这里不好判断是否需要)⇒单一型⇒选项间的关系⇒有包含关系⇒选范围小的,选B!!!错了
-代数-不等式-均值不等式
24、设a, b 是正实数,则
1
a
1\over{a}
a1+
1
b
1\over{b}
b1存在最小值。
(1)已知ab的值。
(2)已知a,b是方程
x
2
−
(
a
+
b
)
x
+
2
=
0
x^2-(a+b)x+2=0
x2−(a+b)x+2=0的两个不同实根。


真题(2020-25)-A-选项特点:两个等号;无法判断是否需要联立;-选项是两个等式,特值法
-优先验证不充分-验证不充分-难度降低-举反例-方法:定性判断-举反例:ad乘积固定,求两数和最大,得:a,b两数差别很大;-A-代数-不等式-均值不等式
25、设a, b, c, d 是正实数,则
a
+
b
≤
2
(
b
+
c
)
\sqrt{a}+\sqrt{b}≤\sqrt{2(b+c)}
a+b≤2(b+c)
(1)
a
+
d
=
b
+
c
a + d = b + c
a+d=b+c
(2)
a
d
=
b
c
ad = bc
ad=bc
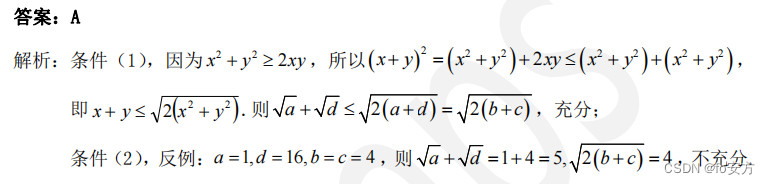

2019
真题(2019-18)A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-几何-解析几何
18、直线
y
=
k
x
y =kx
y=kx 与圆
x
2
+
y
2
−
4
x
+
3
=
0
x^{2}+ y^2−4x+3 =0
x2+y2−4x+3=0 有两个交点
(1)
−
3
3
<
k
<
0
-{\sqrt{3}\over3}<k<0
−33<k<0
(2)
0
<
k
<
2
2
0<k<{\sqrt{2}\over2}
0<k<22


真题(2019-21)-B-边长关系推面积,选B
-几何-平面几何
21、如图,已知正方形 ABCD 面积,O 为 BC 上一点,P 为 AO 的中点,Q 为 DO 上一点,则能确定三角形 PQD 的面积。
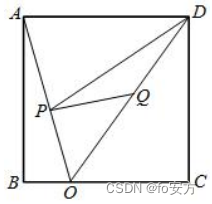
(1)O 为 BC 的三等分点
(2)Q 为 DO 的三等分点


真题(2019-24)-A-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D
-几何-解析几何
24、设三角区域D由直线
x
+
8
y
−
56
=
0
,
x
−
6
y
+
42
=
0
x+8y-56=0,x-6y+42=0
x+8y−56=0,x−6y+42=0与
k
x
−
y
+
8
−
6
k
=
0
(
k
<
0
)
kx-y+8-6k=0(k<0)
kx−y+8−6k=0(k<0)围成,则对任意的
(
x
,
y
)
(x,y)
(x,y),
l
g
(
x
2
+
y
2
)
≤
2
lg(x^2+y^2)≤2
lg(x2+y2)≤2
(1)
k
∈
(
−
∞
,
−
1
]
k∈(-∞,-1]
k∈(−∞,−1]
(2)
k
∈
[
−
1
,
−
1
8
)
k∈[-1,-{1\over8})
k∈[−1,−81)

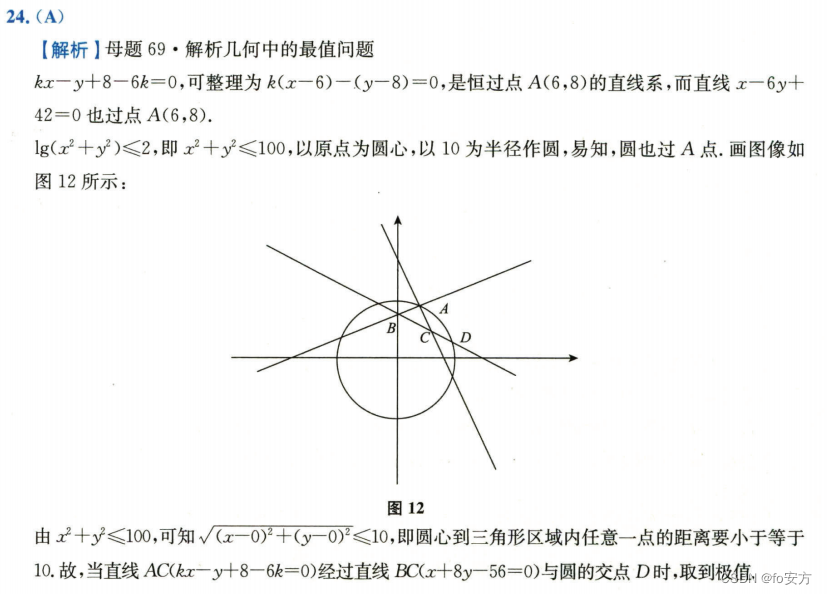

真题(2019-25)-A-选项特点:两个等号;-先分析选项是否需要联合⇒不需要⇒单一型⇒选项间的关系⇒有包含关系,选范围小的,选A;-A-一字之差-两个条件相似程度较高,选信息量少的
-数列-等差数列
25、设数列{
a
n
a_n
an}的前n项和为
S
n
S_n
Sn,则{
a
n
a_n
an}等差
(1)
S
n
=
n
2
+
2
n
,
n
=
1
,
2
,
3
S_n=n^2+2n,n=1,2,3
Sn=n2+2n,n=1,2,3
(2)
S
n
=
n
2
+
2
n
+
1
,
n
=
1
,
2
,
3
S_n=n^2+2n+1,n=1,2,3
Sn=n2+2n+1,n=1,2,3


2018
真题(2018-16)-A-选项特点:两个小于号;-先分析选项是否需要联合⇒不需要(看不出)⇒单一型⇒选项间的关系⇒无共边界反向范围,无包含关系⇒尝试特值法1;两个等号使用特值法;
-代数-不等式-均值不等式
16.设 x, y 为实数,则
∣
x
+
y
∣
≤
2
|x+y|≤2
∣x+y∣≤2
(1)
x
2
+
y
2
≤
2
x^2+y^2≤2
x2+y2≤2
(2)
x
y
≤
1
xy≤1
xy≤1





真题(2018-17)-B-选项特点:两个等号-要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
-B-数列-等差数列-求和公式:
S
n
=
n
(
a
1
+
a
n
)
2
=
n
a
n
+
1
2
(
n
为偶数时,可虚拟小数)
=
n
a
1
+
n
(
n
−
1
)
2
d
=
d
2
n
2
+
(
a
1
−
d
2
)
n
S_n=\frac{n(a_1+a_n)}{2}=na_{\frac{n+1}{2}}(n为偶数时,可虚拟小数)=na_1+\frac{n(n-1)}{2}d=\frac{d}{2}n^2+(a_1-\frac{d}{2})n
Sn=2n(a1+an)=na2n+1(n为偶数时,可虚拟小数)=na1+2n(n−1)d=2dn2+(a1−2d)n
17.{
a
n
a_n
an}等差数列,则能确定
a
1
+
a
2
+
.
.
.
+
a
9
a_1+a_2+...+a_9
a1+a2+...+a9的值。
(1)已知
a
1
a_1
a1的值。
(2)已知
a
5
a_5
a5的值。
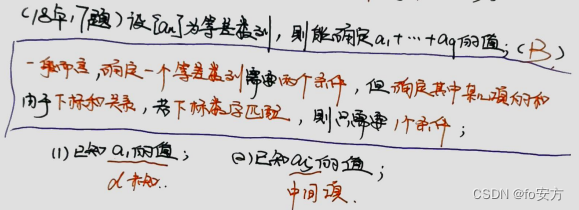




真题(2018-24)-A-选项特点:两个大于号
-几何-解析几何-位置-线圆位置-转换为圆心点到直线距离公式
24.设a, b 实数,则圆
x
2
+
y
2
=
2
y
x^2+y^2=2y
x2+y2=2y与直线
x
+
a
y
=
b
x+ay=b
x+ay=b不相交。
(1)
∣
a
−
b
∣
>
1
+
a
2
|a-b|>\sqrt{1+a^2}
∣a−b∣>1+a2
(2)
∣
a
+
b
∣
>
1
+
a
2
|a+b|>\sqrt{1+a^2}
∣a+b∣>1+a2




2017
真题(2017-17)-A-选项特点:两个等号;
-几何-解析几何-圆的方程
17.圆
x
2
+
y
2
−
a
x
−
b
y
+
c
=
0
x^2+y^2-ax-by+c=0
x2+y2−ax−by+c=0与 x 轴相切,则能确定c 的值。
(1)已知a 的值
(2)已知b 的值
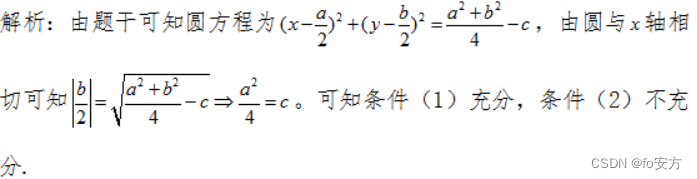

真题(2017-19)-B-选项特点:两个大于号;
-方程-一元二次方程-根的判别式
19.直线
y
=
a
x
+
b
y=ax+b
y=ax+b与抛物线
y
=
x
2
y=x^2
y=x2 有两个交点.
(1)
a
2
>
4
b
a^2>4b
a2>4b
(2) b >0


真题(2017-21)-B-选项特点:两个已知X的值;要素列表法plus-特殊套路-所有圆半径,球半径,均设为需要通过勾股定理求解;即要确定两个要素,需要两个关系;
-B-几何-立体几何
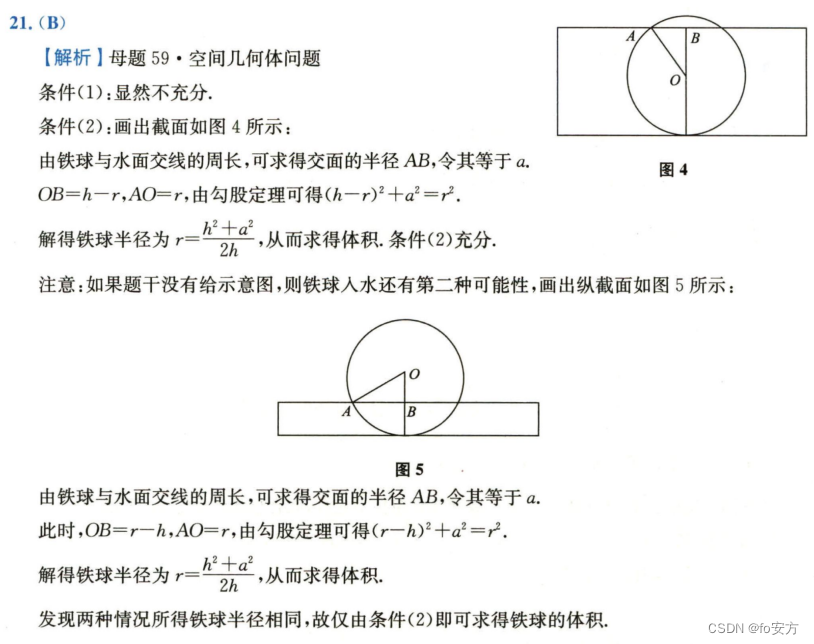
21.如图,一个铁球沉入水池中,则能确定铁球的体积。
(1)已知铁球露出水面的高度。
(2)已知水深及铁球与水面交线的周长。


真题(2017-22)-A
-代数-函数-一元二次函数-最值
22.设a, b 是两个不相等的实数,则函数
f
(
x
)
=
x
2
+
2
a
x
+
b
f(x)=x^2+2ax+b
f(x)=x2+2ax+b 的最小值小于零。
(1)1, a, b成等差数列。
(2)1, a, b成等比数列。


真题(2017-25)-A-选项特点:一个小于号,一个等号;容易误判选C,因为【一个不等号,一个等号,选C】
-算术-绝对值
25.已知a, b, c 为三个实数,则min{
∣
a
−
b
∣
,
∣
b
−
c
∣
,
∣
a
−
c
∣
|a-b|,|b-c|,|a-c|
∣a−b∣,∣b−c∣,∣a−c∣} ≤ 5 .
(1)
∣
a
∣
≤
5
,
∣
b
∣
≤
5
,
∣
c
∣
≤
5
|a|≤5,|b|≤5,|c|≤5
∣a∣≤5,∣b∣≤5,∣c∣≤5
(2)
a
+
b
+
c
=
15
a + b + c = 15
a+b+c=15


2016
真题(2016-16)-B-要素列表法-固有关系-知三推四-总体分为甲乙两部分:①甲部分均值;②乙部分均值;③总体均值;④甲乙三间比例。这四个量中知道三个可求得第四个;-B-数据分析-平均值-加权平均值
16.已知某公司男员工的平均年龄和女员工的平均年龄,则能确定该公司员工的平均年龄。
(1)已知该公司员工的人数。
(2)已知该公司男、女员工的人数之比。


真题(2016-18)-A-选项特点:两个等号;
-方程-出现了两个及以上未知量,而数量关系却少于未知量的个数-整数不定方程-先根据题目转化为ax+by=c形式的不定方程,然后结合整除、倍数和奇偶特征分析讨论求解
18.利用长度为a和b的两种管材能连接成长度为37的管道(单位:米)
(1)a = 3,b = 5
(2)a = 4,b = 6

真题(2016-21)-A-要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;-A-数据分析-平均值与方差-方差是有平方,解出两个根,不能确定;容易误判联立,毕竟均值和方差看着就是一起的。
21.设两组数据
S
1
S_1
S1:3、4、5、6、7和
S
2
S_2
S2:4、5、6、7、a,则能确定a的值。
(1)
S
1
S_1
S1与
S
2
S_2
S2的均值相等。
(2)
S
1
S_1
S1与
S
2
S_2
S2的方差相等。

真题(2016-23)-B-选项特点:两个等号;要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;两个等号用特值法
B-代数-整式-立方公式-和与差的立方:
a
3
±
b
3
=
(
a
±
b
)
(
a
2
∓
a
b
+
b
2
)
a^3±b^3=(a±b)(a^2∓ab+b^2)
a3±b3=(a±b)(a2∓ab+b2);-代数-不等式-均值不等式
23.设 x, y 是实数,则可以确定
x
3
+
y
3
x^3+y^3
x3+y3的最小值
(1)
x
y
=
1
xy=1
xy=1
(2)
x
+
y
=
2
x+y=2
x+y=2


与立方有关的公式
和与差的立方:
a
3
±
b
3
=
(
a
±
b
)
(
a
2
∓
a
b
+
b
2
)
a^3±b^3=(a±b)(a^2∓ab+b^2)
a3±b3=(a±b)(a2∓ab+b2)
①立方和:
a
3
+
b
3
=
(
a
+
b
)
(
a
2
−
a
b
+
b
2
)
a^3+b^3=(a+b)(a^2-ab+b^2)
a3+b3=(a+b)(a2−ab+b2)——【
x
3
+
1
=
(
x
+
1
)
(
x
2
−
x
+
1
)
x^3+1=(x+1)(x^2-x+1)
x3+1=(x+1)(x2−x+1)】——【三次和=一次和与二次和乘积,其中二次和要减一次积,三次喝=一次喝,二次喝见一刺激;二次核检一次记;三次核检=一次核检乘以二次核减见一次记;三次去喝酒=一次喝酒×二次喝酒被记录一次】
②立方差:
a
3
−
b
3
=
(
a
−
b
)
(
a
2
+
a
b
+
b
2
)
a^3-b^3=(a-b)(a^2+ab+b^2)
a3−b3=(a−b)(a2+ab+b2)——【
x
3
−
1
=
(
x
−
1
)
(
x
2
+
x
+
1
)
x^3-1=(x-1)(x^2+x+1)
x3−1=(x−1)(x2+x+1)】
③拓展:
x
n
−
y
n
=
(
x
−
y
)
(
x
n
−
1
+
x
n
−
2
y
+
x
n
−
3
y
2
+
.
.
.
+
y
n
−
1
)
x^n-y^n=(x-y)(x^{n-1}+x^{n-2}y+x^{n-3}y^2+...+y^{n-1})
xn−yn=(x−y)(xn−1+xn−2y+xn−3y2+...+yn−1)
完全立方:
(
a
±
b
)
3
=
a
3
±
3
a
2
b
+
3
a
b
2
±
b
3
(a±b)^3=a^3±3a^2b+3ab^2±b^3
(a±b)3=a3±3a2b+3ab2±b3——【每项都有3】
①和立方:
(
a
+
b
)
3
=
a
3
+
b
3
+
3
a
2
b
+
3
a
b
2
=
a
3
+
b
3
+
3
a
b
(
a
+
b
)
(a+b)^3=a^3+b^3+3a^2b+3ab^2=a^3+b^3+3ab(a+b)
(a+b)3=a3+b3+3a2b+3ab2=a3+b3+3ab(a+b)——【和立方比立方和多3倍乘积乘和】——【和立方=立方和+3倍乘积乘和】——【和的三次=三次和+三鸡和】
②差立方:
(
a
−
b
)
3
=
a
3
−
b
3
−
3
a
2
b
+
3
a
b
2
=
a
3
−
b
3
−
3
a
b
(
a
−
b
)
(a-b)^3=a^3-b^3-3a^2b+3ab^2=a^3-b^3-3ab(a-b)
(a−b)3=a3−b3−3a2b+3ab2=a3−b3−3ab(a−b)——【差立方比立方差少3倍乘积乘差】——【差立方=立方差-3倍乘积乘差】
真题(2016-24)-A-要素列表法plus-特殊套路-一次与二次-大前提一元等式+一次条件 vs 二次条件 ⟹ 选一次条件;
-A-代数-数列-递推公式-直接计算法
24.已知数列
a
1
,
a
2
,
a
3
,
.
.
.
,
a
10
a_1,a_2,a_3,...,a_{10}
a1,a2,a3,...,a10,则
a
1
−
a
2
+
a
3
−
.
.
.
+
a
9
−
a
10
≥
0
a_1-a_2+a_3-...+a_9-a_{10}≥0
a1−a2+a3−...+a9−a10≥0
(1)
a
n
≥
a
n
+
1
,
n
=
1
,
2
,
.
.
.
,
9
a_n≥a_{n+1},n=1,2,...,9
an≥an+1,n=1,2,...,9
(2)
a
n
2
≥
a
n
+
1
2
,
n
=
1
,
2
,
.
.
.
,
9
a_n^2≥a_{n+1}^2,n=1,2,...,9
an2≥an+12,n=1,2,...,9

2015
真题(2015-17)-A;-选项特点:两个大于等于号;
-代数-不等式
17.已知a, b 为实数,则
a
≥
2
a ≥ 2
a≥2 或
b
≥
2
b ≥ 2
b≥2
(1)
a
+
b
≥
4
a + b ≥ 4
a+b≥4
(2)
a
b
≥
4
ab ≥ 4
ab≥4


真题(2015-18)-B;两个等号用特值法,但是这题用不了
-代数-整式分式
18. 已知 p, q 为非零实数. 则能确定
p
q
(
p
−
1
)
\frac{p}{q(p-1)}
q(p−1)p的值.
(1)
p
+
q
=
1
p+q=1
p+q=1
(2)
1
p
+
1
q
=
1
\frac{1}{p}+\frac{1}{q}=1
p1+q1=1
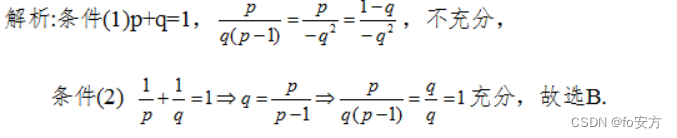

真题(2015-19)-B-选项特点:两个等号;
-数据分析-概率-已知元素的数量求概率⟹ 古典概型⟹ 两个排列组合相除计算概率或穷举法⟹ 分母是C运算,分子数量少用穷举,数量多用C运算
19. 信封中装有10 张奖券,只有1张有奖从信封中同时抽取2 张奖券,中奖的概率为 P ;从信封中每次抽取1张奖券后放回,如此重复抽取n 次,中奖的概率为Q ,则
P
<
Q
P<Q
P<Q。
(1)
n
=
2
n=2
n=2
(2)
n
=
3
n=3
n=3

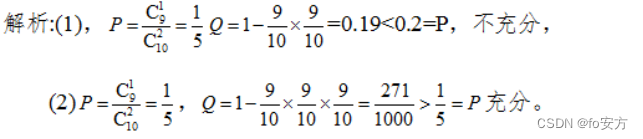
不联立条件秒杀:条件(1)和条件(2)不能联立,选数值大的。如n=2,n=3,选n=3。
包含选项+定性判断秒杀:第一步:定性判断:题干“重复抽取n次,每抽取1张后放回”,得:Q与n正相关,递增关系。结论“P<Q”,得:Q越大越好,得:n越大越好。属于包含型选项题,数值越大越充分,由条件得:条件(1)包含于条件(2),选B或D,80%选B,20%选D。

真题(2015-21)-B-两个大于号;
-实数
21.已知
M
=
(
a
1
+
a
2
+
.
.
.
+
a
n
−
1
)
(
a
2
+
a
3
+
.
.
.
+
a
n
)
M=(a_1+a_2+...+a_{n-1})(a_2+a_3+...+a_n)
M=(a1+a2+...+an−1)(a2+a3+...+an),
N
=
(
a
1
+
a
2
+
.
.
.
+
a
n
)
(
a
2
+
a
3
+
.
.
.
+
a
n
−
1
)
N=(a_1+a_2+...+a_n)(a_2+a_3+...+a_{n-1})
N=(a1+a2+...+an)(a2+a3+...+an−1),则M>N。
(1)
a
1
>
0
a_1>0
a1>0
(2)
a
1
a
n
>
0
a_1a_n>0
a1an>0

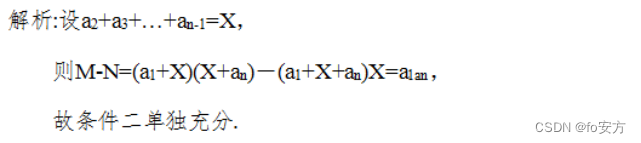
2014
真题(2014-16)-A
-方程
16.已知曲线
l
l
l:
y
=
a
+
b
x
−
6
x
2
+
x
3
y=a+bx-6x^2+x^3
y=a+bx−6x2+x3,则
(
a
+
b
−
5
)
(
a
−
b
−
5
)
=
0
(a+b-5)(a-b-5)=0
(a+b−5)(a−b−5)=0 .
(1)曲线
l
l
l过点
(
1
,
0
)
(1,0)
(1,0)
(2)曲线
l
l
l过点
(
−
1
,
0
)
(-1,0)
(−1,0)


真题(2014-17)-选项特点:一个大于,一个小于;B-特值体系法-三、无解/恒成立型特值;-选项有取值范围⇒分三种情况⇒取值范围有交集选C⇒取值范围共边界但反向选A⇒取值范围不相邻,相加非全集选D,但是错了!!!!!
-B-代数-不等式-绝对值不等式;-代数-一元二次不等式-恒成立
17.不等式
∣
x
2
+
2
x
+
a
∣
≤
1
|x^2+2x+a|≤1
∣x2+2x+a∣≤1的解集为空集。
(1)
a
<
1
a<1
a<1
(2)
a
>
2
a>2
a>2


方法二:见“
x
2
x^2
x2”首选配平方。
∣
x
2
+
2
x
+
1
+
a
−
1
∣
≤
1
|x^2+2x+1+a-1|≤1
∣x2+2x+1+a−1∣≤1,得:
∣
(
x
+
1
)
2
+
∣
a
−
1
∣
∣
>
1
|(x+1)^2+|a-1||>1
∣(x+1)2+∣a−1∣∣>1,得:
(
x
+
1
)
2
≥
0
(x+1)^2≥0
(x+1)2≥0,
a
−
1
>
1
a-1>1
a−1>1得:
a
−
1
>
1
a-1>1
a−1>1,得:
a
>
2
a>2
a>2。

真题(2014-19)-A-选项特点:两个等号;要素列表法plus-特殊套路-一次与二次-条件偶次+结论奇次⟹不充分;
-代数-分式;-代数-整式-立方公式-和与差的立方:
a
3
±
b
3
=
(
a
±
b
)
(
a
2
∓
a
b
+
b
2
)
a^3±b^3=(a±b)(a^2∓ab+b^2)
a3±b3=(a±b)(a2∓ab+b2)
19.设 x 是非零实数,则
x
3
+
1
x
3
=
18
x^3+\frac{1}{x^3}=18
x3+x31=18
(1)
x
+
1
x
=
3
x+\frac{1}{x}=3
x+x1=3
(2)
x
2
+
1
x
2
=
7
x^2+\frac{1}{x^2}=7
x2+x21=7



真题(2014-20)-A-选项特点:两个已知X的值;
-几何-平面几何-圆
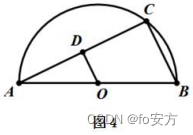
20.如图 4 所示,O 是半圆的圆心,C是半圆上的一点,OD⊥AC,则能确定OD 的长。
(1)已知BC的长。
(2)已知AO的长。


真题(2014-21)-A-容易误判C,因为【一个定量,一个定性】
-方程-一元二次方程-判别式-
△
=
b
2
−
4
a
c
△=b^2-4ac
△=b2−4ac
21.方程
x
2
+
2
(
a
+
b
)
x
+
c
2
=
0
x^2+2(a+b)x+c^2=0
x2+2(a+b)x+c2=0 有实根。
(1) a, b, c 是一个三角形的三边长。
(2)实数a, b, c 成等差数列。


真题(2014-25)-A-两个大于号
-几何-解析几何-最值
25.已知 x, y 为实数,则
x
2
+
y
2
=
1
x^2+y^2=1
x2+y2=1.
(1)
4
y
−
3
x
≥
5
4y - 3x ≥ 5
4y−3x≥5
(2)
(
x
−
1
)
2
+
(
y
−
1
)
2
≥
5
(x-1)^2+(y-1)^2≥5
(x−1)2+(y−1)2≥5


2013
真题(2013-16)-A-两个等号
-几何-解析几何-面积
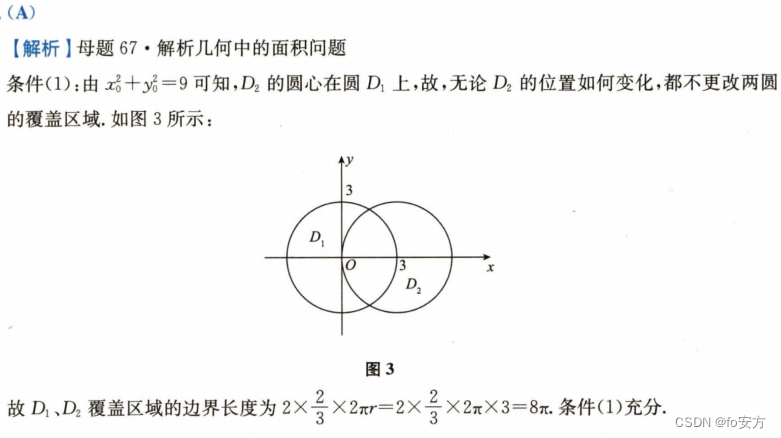
16.已知平面区域D1={
(
x
,
y
)
∣
x
2
+
y
2
≤
9
{(x,y)|x^2+y^2≤9}
(x,y)∣x2+y2≤9},D2={
(
x
,
y
)
∣
(
x
−
x
0
)
2
+
(
y
−
y
0
)
2
≤
9
{(x,y)|(x-x_0)^2+(y-y_0)^2≤9}
(x,y)∣(x−x0)2+(y−y0)2≤9},则
D
1
,
D
2
D1,D2
D1,D2覆盖区域的边界长度为
8
π
8π
8π。
(1)
x
0
2
+
y
0
2
=
9
x_0^2+y_0^2=9
x02+y02=9
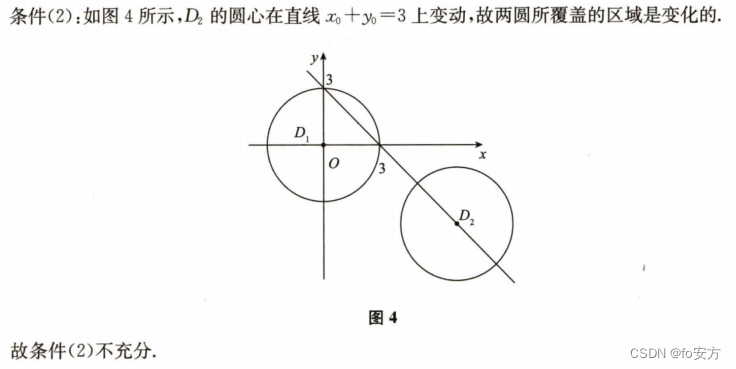
(2)
x
0
+
y
0
=
3
x_0+y_0=3
x0+y0=3
真题(2013-18)-B-两个等号
-几何-平面几何-三角形的形状判断
18.△ABC 的边长分别为a, b, c ,则△ABC 为直角三角形。
(1)
(
c
2
−
a
2
−
b
2
)
(
a
2
−
b
2
)
=
0
(c^2-a^2-b^2)(a^2-b^2)=0
(c2−a2−b2)(a2−b2)=0
(2)△ABC 的面积为
1
2
a
b
\frac{1}{2}ab
21ab

真题(2013-19)-A-选项特点:两个等号;-特值法体系-两项特值与三项特值;-A-代数-函数-一元二次函数-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
19.已知二次函数
f
(
x
)
=
a
x
2
+
b
x
+
c
f(x)=ax^2+bx+c
f(x)=ax2+bx+c,则方程为
f
(
x
)
=
0
f(x)=0
f(x)=0有两个不同实根。
(1)
a
+
c
=
0
a+c=0
a+c=0
(2)
a
+
b
+
c
=
0
a + b + c = 0
a+b+c=0


真题(2013-23)-B
-应用题-最值
23.某单位年终奖共发了100万元奖金,奖金金额分别是一等奖1.5万元、二等奖1万元、三等奖0.5万元,则该单位至少有100人。
(1)得二等奖的人数最多。
(2)得三等奖的人数最多。

真题(2013-24)-A
-数据分析-排列组合-不同元素的分配
24.三个科室的人数分别为6、3和2,因工作需要,每晚需要排3人值班,则在两个月中以便每晚值班人员不完全相同。
(1)值班人员不能来自同一科室。
(2)值班人员来自三个不同科室。