文章目录
- 方程组的几何解释
- 矩阵消元
- 乘法和逆矩阵
- A的LU分解
- 转置-置换-向量空间R
- 列空间和零空间
- 求解Ax=0主变量 特解
- 求解Ax=b可解性和解的结构
- 线性相关性、基、维数
- 四个基本子空间
- 矩阵空间、秩1矩阵和小世界图
- 图和网络
- 复习一
方程组的几何解释
线性组合:
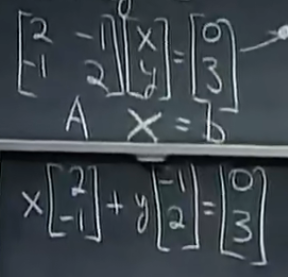
找到合适的x和y的线性组合,从而让col1和col2组合得到结果b向量

3x3矩阵:

对于任何b都有Ax = b吗? == 列的线性组合能否覆盖整个三维空间?
三个向量(A的三个列)在同一平面时不行
两种方法的矩阵乘法:
按列求:
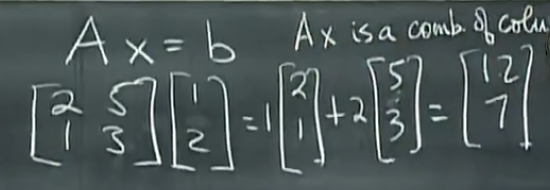
按行求:一行乘一列
A乘以x看作A各列的线性组合
矩阵消元
矩阵消元:
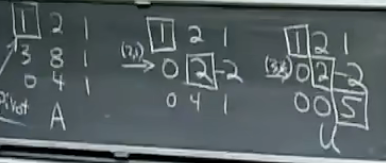
U是A的最终结果
增广矩阵:

c是b的最终结果
矩阵x列=列
行x矩阵=行
B的第二行减去3倍的第一行:
A x B = C
A第一行a为1,bc为0=取B的第一行1倍,其他行不取
A第二行a为-3,b为1=取B的第一行的-3倍,第二行的1倍,二者相加
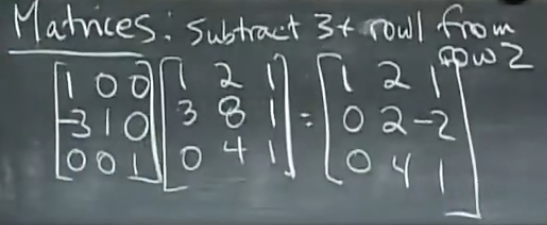
A为初等矩阵E21
E
32
(
E
21
A
)
=
U
(
E
32
E
21
)
A
=
U
\begin{aligned} E_{32}(E_{21}A) &= U\\ (E_{32}E_{21})A &= U \end{aligned}
E32(E21A)(E32E21)A=U=U
交换列:
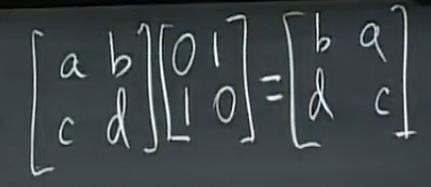
E x A 变换行,A x E变换列
逆变换:
行二减去三倍行一 => 行二加上三倍行一
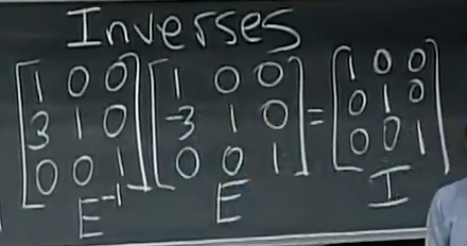
乘法和逆矩阵
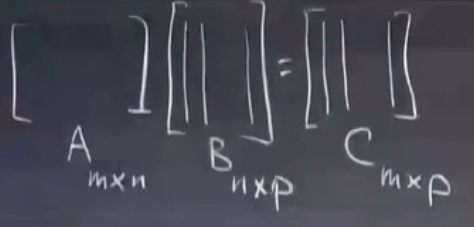
A乘以 B的各个列向量 得到C的列向量 = C中各列是A中各列的线性组合
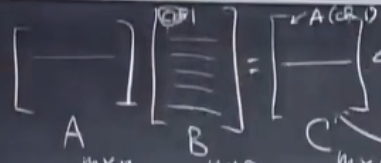
A乘以 B的各个行向量 得到C的行向量 = C中各行是B中各行的线性组合
如:A中某行的各个值(1 2 3)等于B中各行
[
a
b
c
d
e
f
g
h
i
]
\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}
adgbehcfi
的对应倍数
a
b
c
2
d
2
e
2
f
3
g
3
h
3
i
\begin{matrix} a & b & c \\ 2d & 2e & 2f \\ 3g & 3h & 3i \end{matrix}
a2d3gb2e3hc2f3i
相加(a+2d+3g b+2e+3h c+2f+3i)就是C的对应行
列同理
求矩阵相乘有四种方法:
- 常规方法:一行乘一列得一个值
- 列方法:C的列是A的各列的线性组合,一次求一列
- 行方法:C的行是B的各行的线性组合,一次求一行
- 列乘行:
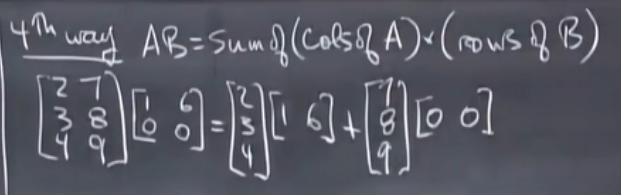
- 分块:
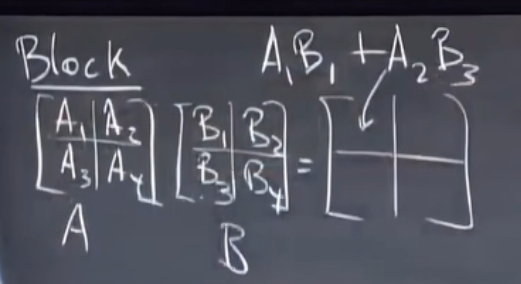
对于方阵:
A
−
1
A
=
I
=
A
A
−
1
A^{-1}A=I=AA^{-1}
A−1A=I=AA−1
矩阵没有逆:
- 无法通过线性组合矩阵的各行得到(1 0 0 …)等等单位矩阵的各行(行方向在同一直线上),列同理
- 满足
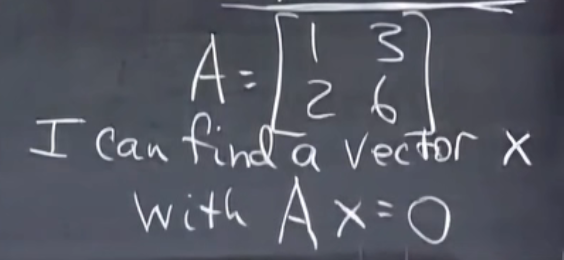 这样的矩阵没有逆(x不是0向量)
这样的矩阵没有逆(x不是0向量)
如果矩阵其中一列对线性组合毫无贡献,矩阵不可能有逆
高斯-若尔当消元:
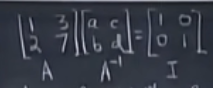
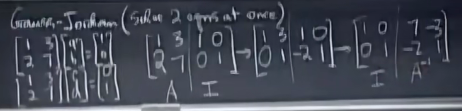
E
[
A
I
]
=
[
I
?
]
E
A
=
I
tell us
E
=
A
−
1
E\begin{bmatrix}A & I\end{bmatrix} =\begin{bmatrix}I & ?\end{bmatrix}\\ EA=I \\ \text{tell us} \\ E=A^{-1}
E[AI]=[I?]EA=Itell usE=A−1
A的LU分解
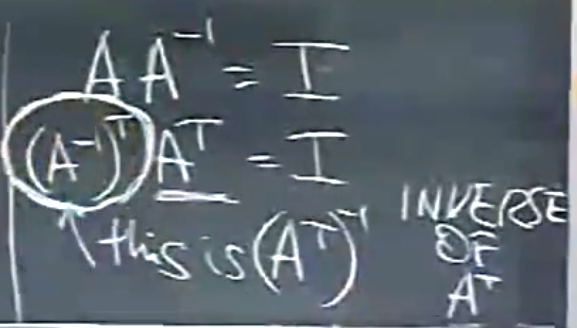
A的转置的逆等于A的逆的转置
E
A
=
U
E
[
2
1
8
7
]
=
[
2
1
0
3
]
\begin{aligned} EA &= U \\ E \begin{bmatrix} 2 & 1\\ 8 & 7 \end{bmatrix} &= \begin{bmatrix} 2 & 1\\ 0 & 3 \end{bmatrix} \end{aligned}
EAE[2817]=U=[2013]
A = L U [ 2 1 8 7 ] = L [ 2 1 0 3 ] \begin{aligned} A &= LU\\ \begin{bmatrix} 2 & 1\\ 8 & 7 \end{bmatrix} &=L \begin{bmatrix} 2 & 1\\ 0 & 3 \end{bmatrix} \end{aligned} A[2817]=LU=L[2013]
可见
E
=
E
1
E
2
E
3
L
=
E
−
1
L
=
E
3
−
1
E
2
−
1
E
1
−
1
E = E_{1}E_{2}E_{3}\\ L = E^{-1}\\ L = E_{3}^{-1}E_{2}^{-1}E_{1}^{-1}
E=E1E2E3L=E−1L=E3−1E2−1E1−1
在该例中,L为
[
1
0
4
1
]
\begin{bmatrix} 1 & 0\\ 4 & 1 \end{bmatrix}
[1401]
对角线为1的下三角阵(lower),U为对角线上是主元的上三角阵(upper)
将主元单拎出来:
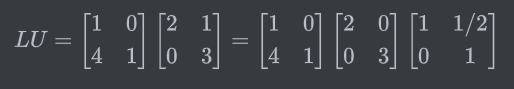
这里,4是消元乘数,那么:
如果没有行交换,消元乘数可以直接写入单位矩阵中组成L
nxn矩阵的消元需要
n
2
+
(
n
−
1
)
2
+
(
n
−
2
)
2
+
⋯
+
2
2
+
1
2
n^2+(n-1)^2+(n-2)^2+\dots+2^2+1^2
n2+(n−1)2+(n−2)2+⋯+22+12
次操作(不是行操作而是值操作)
置换矩阵:其逆等于其转置
转置-置换-向量空间R
上一节讨论不需要行交换的情况,对于行需要交换的:
P
A
=
L
U
PA=LU
PA=LU
P即为置换矩阵,将A的行交换成正确的样子的、行重新排列了的单位矩阵
nxn置换矩阵的个数:n!
置换矩阵可逆,且其逆等于其转置
转置:(AT)i,j=Aj,i
对称矩阵:转置后等于自身
所有RTR结果都是对称矩阵:
(
R
T
R
)
T
=
R
T
R
(R^TR)^T=R^TR
(RTR)T=RTR
向量空间必须要对数乘封闭,即一个向量乘以任何数都在这个向量空间内,此时向量空间为一条该向量所在的直线(子空间),过原点(因为要允许乘0)
子空间是向量空间内的向量空间,即某些向量在母空间,而其本身也构成向量空间
R2的子空间:
- R2平面
- 任意过原点的直线
- 0原点
R3的子空间:
- R3空间
- 任意过原点的平面
- 任意过原点的直线
- 0原点
对于一个矩阵,它的列的任意一种线性组合而成的向量都在向量子空间,又称列空间
列空间和零空间
空间中有平面P和直线L两向量空间,两者相交于原点,两者的并集不构成向量空间,因为对于并集中的向量相加,结果不在并集中:对加法不封闭。而交集构成向量空间。
向量加法和数乘是子空间中必须封闭的运算
A是4x3矩阵,那么A的列空间就是R4的子空间,由所有列的线性组合构成,换句话说,只有当b为A中各列的线性组合时,b才是Ax=b的解,此时b在A的列空间内
线性无关:A中各列进行线性组合,其中每一列都对组合有所贡献,换句话说,无法去掉某列得到相同的列空间,有贡献的列称为主列
零空间:x构成的向量空间(因为Av=0,Aw=0,A(v+w)=0,vw加和还在范围内,所以构成向量空间),使得Ax=0,此时x可以取数乘cx,在R3中表示为一条过原点的直线
而对于Ax=b,b!=0,解x必须包含0才能构成向量空间,因为所有向量空间必须过原点
求解Ax=0主变量 特解
消元不改变零空间(方程组解)
消元后非主元所在列对应的未知量为自由变量,表示可以自由取值。
秩 = 主元个数
特解:自由变量取值后,连带产生的解的任意倍
特解的线性组合(任意倍、相加)就是零空间
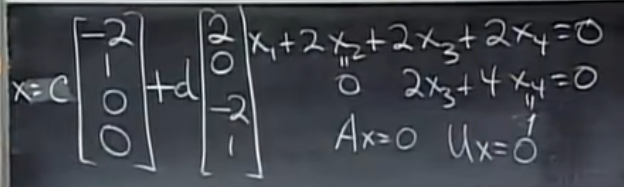
简化行阶梯型矩阵:主元上下都是0
经典行简化阶梯型(行交换后):
R
=
[
I
F
0
0
]
R = \begin{bmatrix} I & F\\ 0 & 0 \end{bmatrix}
R=[I0F0]
要求x就是求:
R
x
=
0
Rx=0
Rx=0
x由多个特解线性组合而成,这些特解作为列构成的矩阵叫做零空间矩阵N,此时
R
N
=
0
[
I
F
0
0
]
[
−
F
I
]
=
0
\begin{aligned} RN &= 0 \\ \begin{bmatrix} I & F\\ 0 & 0 \end{bmatrix} \begin{bmatrix} -F \\ I \end{bmatrix} &=0 \end{aligned}
RN[I0F0][−FI]=0=0
这样就能快速找到零基(F的列数决定I的列数)
求解Ax=b可解性和解的结构
Ax=b仅当b属于A的列空间时成立
A的行的线性组合产生了零行,则相同的线性组合将让b也产生0
特解:增广矩阵消元后保证零行等于0,然后指定自由变量为0,求出一个特解xp
通解:x=xp+xn,特解加零特解的线性组合
A
x
p
=
b
A
x
n
=
0
A
(
x
p
+
x
n
)
=
b
Ax_p=b\\ Ax_n=0\\ A(x_p+x_n)=b
Axp=bAxn=0A(xp+xn)=b
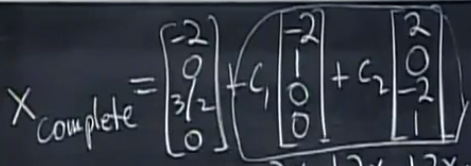
其间的关系有点类似于二维直线y=a+cx,y=cx过原点,y=a+cx移动a过a。这个解的图像也是后面零解过原点(因为是零空间)而加上特解,则过特解
列满秩r=n:没有自由变量,也就是没有F,所以求零解时不能自由赋值,此时零空间N(A)只有零向量,Ax=b的解空间如果解存在则只有唯一解x=xp
行满秩r=m:消元时没有零行,那么对于任意b,Ax=b都有解。自由变量为n-r个
方阵满秩r=m=n:可逆矩阵,零空间只包含零向量,Ax=b有解

矩阵的秩决定了方程组解的数目
线性相关性、基、维数
线性相关性:向量组中有0个向量的话一定相关,因为
0
⋅
v
1
+
0
⋅
v
2
+
n
⋅
0
=
0
0 \cdot v_1 + 0 \cdot v_2 + n \cdot 0 = 0
0⋅v1+0⋅v2+n⋅0=0
组合(非零组合 0 0 n)得到0向量
A
=
[
v
1
v
2
…
v
n
]
A= \begin{bmatrix} v_1 & v_2 & \dots & v_n \end{bmatrix}
A=[v1v2…vn]
若v1,v2,…,vn不相关,则零空间只有0向量,r=n无自由变量。反之若Ac=0,c != 0,则相关,r < n有自由变量
向量"生成"(span)空间:空间包含这些向量的所有线性组合(最小)
向量空间的一组"基":一组1. 线性无关 2. 生成整个空间 的向量——主列
当nxn方阵可逆时,其向量空间为Rn
对于给定空间,空间中任意一组基的向量数目相等,此处的基向量数目就是维数
(列)空间的维数 <=> 基向量组成的矩阵的rank
已知维数,有一些线性无关的向量,则其中维数个向量组成一组基
零空间的维数 = 自由变量个数
四个基本子空间
对于mxn矩阵的四个基本子空间:
- 列空间C(A):A的列的所有线性组合,在Rm中
- 零空间N(A):在Rn中
- 行空间C(AT):A的行的所有线性组合,在Rn中
- 左零空间N(AT):在Rm
列向量矩阵的秩 = 行向量的矩阵的秩 = r = 主元数
列空间的维数 = 行空间的维数 = r
零空间的维数 = n - r
左零空间的维数 = m - r
n - r :特解个数
行变换下影响行空间,但影响列空间
行空间的基 = 行最简型R的前r行
左零空间:
为什么叫左零空间:
A
T
y
=
0
y
T
A
=
0
A^Ty=0 \\ y^TA=0
ATy=0yTA=0
左零空间的基:
化行简化型
r r e f [ A I ] → [ R E ] rref \begin{bmatrix} A & I \end{bmatrix}\rightarrow \begin{bmatrix} R & E \end{bmatrix} rref[AI]→[RE]
E A = R EA=R EA=R
此时R中的零行对应的E中的行即为左零空间的基
eg:
[
−
1
2
0
1
−
1
0
(
1
0
1
)
]
A
=
[
1
0
1
1
0
1
1
0
(
0
0
0
0
)
]
\begin{bmatrix} -1 & 2 & 0 \\ 1 & -1 & 0 \\ (1 & 0 & 1) \end{bmatrix} A= \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ (0 & 0 & 0 & 0) \end{bmatrix}
−11(12−10001)
A=
10(0010110100)
矩阵服从向量空间的运算率,可以把矩阵看作"向量",虽然矩阵可相乘,但把矩阵看作向量空间时,只考虑相加、数乘
此处,对角线矩阵空间的一个基为
[
1
0
0
0
0
0
0
0
0
]
,
[
1
0
0
0
2
0
0
0
0
]
,
[
0
0
0
0
0
0
0
0
1
]
\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{bmatrix}, \begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 0\\ \end{bmatrix}, \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix}
100000000
,
100020000
,
000000001
矩阵空间、秩1矩阵和小世界图
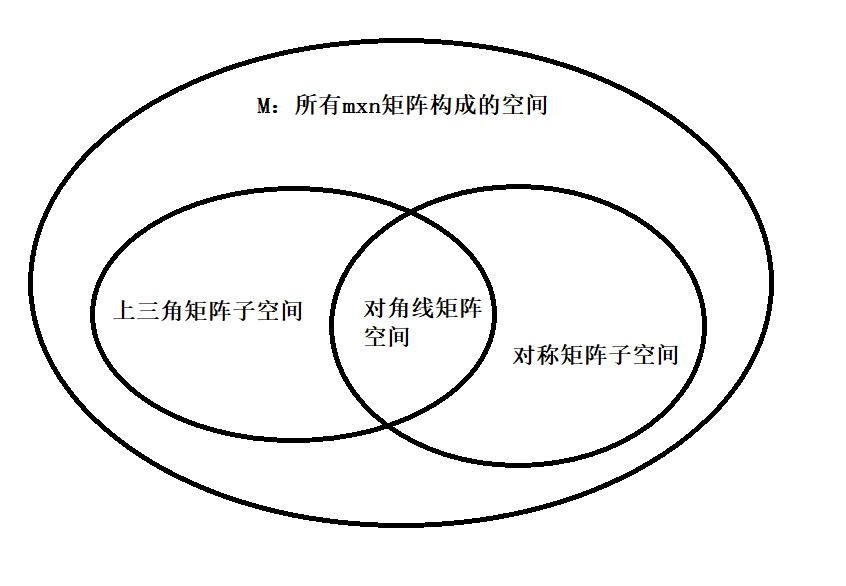
以3x3矩阵为例,M为所有3x3矩阵构成空间
需要9个矩阵:
[
1
0
0
0
0
0
0
0
0
]
,
[
0
1
0
0
0
0
0
0
0
]
,
…
,
[
0
0
0
0
0
0
0
0
1
]
\begin{bmatrix} 1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{bmatrix}, \begin{bmatrix} 0 & 1 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{bmatrix},\dots, \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 1\\ \end{bmatrix}
100000000
,
000100000
,…,
000000001
构成一组基
M的维度为9,对称矩阵空间(S)维度=6,上三角矩阵空间(U)维度=6
维度
d
i
m
(
更小的子空间
S
∪
U
)
=
3
\text{维度}dim(\text{更小的子空间}S \cup U)=3
维度dim(更小的子空间S∪U)=3
当S∪U时,产生的不是子空间,需要补充:S+U (S和U的组合)取S的任一矩阵+U的任一矩阵 。这里的空间包含所有3x3矩阵
d
i
m
(
S
+
U
)
=
9
dim(S+U)=9
dim(S+U)=9
d i m ( S ) + d i m ( U ) = d i m ( S ∪ U ) + d i m ( S + U ) dim(S)+dim(U)=dim(S \cup U)+dim(S+U) dim(S)+dim(U)=dim(S∪U)+dim(S+U)
秩1矩阵:如
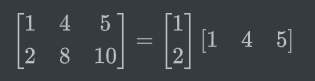
可以把秩为4的矩阵分解为4个秩1矩阵
而两个秩为4的矩阵相加结果的秩通常不为4
行空间维数+零空间维数=行数
列空间维数+左零空间维数=列数
小世界图:“六分度猜想”,每个人至多通过六个人可以认识任何人,这样一个人与人的关系图
图和网络
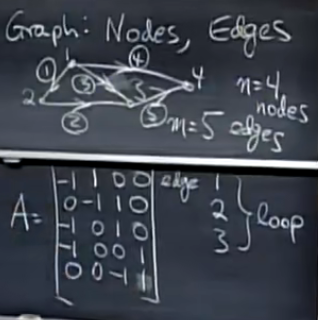
与回路对应的行是线性相关的,如第1、2、3行
对于这样的矩阵的零空间Ax=0,将x视为结点电势,则结果: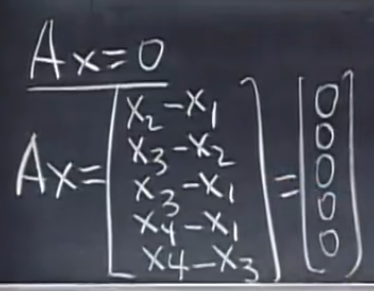
可以看作结点间电势差,此时各点电势差为零,节点间没有电流
xi-xj电势差通过欧姆定律得到结点间电流y,对于左零空间ATy=0,即基尔霍夫电流定律(KCL)
对于左零空间的基,表现为满足基尔霍夫电流定律(流入=流出)的一组向量,每个元素是结点电流:
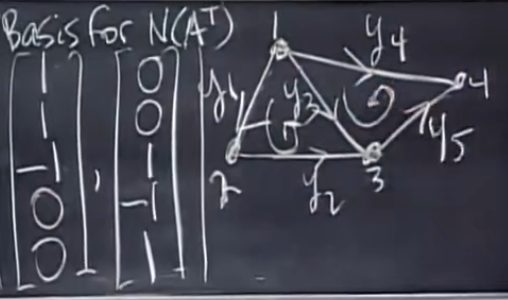
这里两个向量是无关的,即两个回路不产生嵌套,大的外城回路由两个小的回路组成
矩阵的主行对应的边组成了个没有回路的图(树),相关性均源自于回路
d
i
m
N
(
A
T
)
=
m
−
r
相互无关的回路数量loops
=
边的数量edges
−
(
结点数量nodes
−
1
)
n
o
d
e
s
−
e
d
g
e
s
+
l
o
o
p
s
=
1
(欧拉公式)
\begin{aligned} dim N(A^T) &= m-r\\ \text{相互无关的回路数量loops} &= \text{边的数量edges}-(\text{结点数量nodes}-1)\\ nodes - edges + loops &= 1 (欧拉公式) \end{aligned}
dimN(AT)相互无关的回路数量loopsnodes−edges+loops=m−r=边的数量edges−(结点数量nodes−1)=1(欧拉公式)
r=n-1(n为结点数即列数)
回到电路
[
x
i
−
x
j
…
]
⇒
e
=
A
x
电势差
[
e
1
…
]
⇒
y
=
C
e
电流
[
y
1
…
]
\begin{bmatrix} x_i-x_j\\ \dots \end{bmatrix} \Rightarrow ^{e=Ax} \text{电势差}\begin{bmatrix} e_1\\ \dots \end{bmatrix} \Rightarrow ^{y=Ce} \text{电流}\begin{bmatrix} y_1\\ \dots \end{bmatrix}
[xi−xj…]⇒e=Ax电势差[e1…]⇒y=Ce电流[y1…]
总的来说:
A
T
C
A
x
=
f
加上电流源
A^TCAx=f\text{加上电流源}
ATCAx=f加上电流源
复习一
已知 A x = [ 2 4 2 ] , 通解 x = [ 2 0 2 ] + c [ 1 1 0 ] + d [ 0 0 1 ] 已知Ax= \begin{bmatrix} 2 \\ 4 \\ 2 \end{bmatrix} ,通解x= \begin{bmatrix} 2 \\ 0 \\ 2 \end{bmatrix}+ c\begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}+ d\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} 已知Ax= 242 ,通解x= 202 +c 110 +d 001
求行空间的维数:r=n-dimN(A)=n-2=1 (n可由b知为3)
求A,将特解(2 0 2)代入Ax=(2 4 2),得a1=(1 2 1)
将特解(1 1 0)代入Ax=0,得a2=(-1 -2 -1)
将特解(0 0 1)代入Ax=0,得a3=(0 0 0)
使Ax=b成立的b的条件:b是A中列向量的线性组合
所有同阶可逆矩阵不能组成子空间,因为可逆矩阵相加不能保证结果可逆
B
2
=
0
⇏
B
=
0
B
=
[
0
1
0
0
]
B^2=0 \nRightarrow B=0 \\ B= \begin{bmatrix} 0 & 1\\ 0 & 0 \end{bmatrix}
B2=0⇏B=0B=[0010]
nxm,满秩矩阵Ax=b(可逆),对任意b有解
若C可逆,N(CD)=N(D)
已知
B
=
C
D
=
[
1
1
0
0
1
0
1
0
1
]
[
1
0
−
1
2
0
1
1
−
1
0
0
0
0
]
已知B=CD= \begin{bmatrix} 1 & 1 & 0\\ 0 & 1 & 0\\ 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -1 & 2\\ 0 & 1 & 1 & -1\\ 0 & 0 & 0 & 0 \end{bmatrix}
已知B=CD=
101110001
100010−1102−10
不计算B,求B零空间的基(即N(D))
b
a
s
i
s
=
[
1
−
2
−
1
1
1
0
0
1
]
basis= \begin{bmatrix} 1 & -2\\ -1 & 1\\ 1 & 0\\ 0 & 1 \end{bmatrix}
basis=
1−110−2101
v = [ 1 2 3 ] 不能既是 A 的一行,又在 A 的零空间内 [ X X X 1 2 3 X X X ] [ 1 2 3 ] ≠ [ 0 0 0 ] v=\begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix} 不能既是A的一行,又在A的零空间内\\ \begin{bmatrix} X & X & X\\ 1 & 2 & 3\\ X & X & X \end{bmatrix} \begin{bmatrix} 1\\ 2\\ 3 \end{bmatrix}\not= \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} v= 123 不能既是A的一行,又在A的零空间内 X1XX2XX3X 123 = 000
行空间和零空间的交集只有零向量