力扣日记12.19-【二叉树篇】二叉搜索树中的搜索

news2024/9/30 5:28:15

力扣日记：【二叉树篇】二叉搜索树中的搜索

日期：2023.12.19
参考：代码随想录、力扣

700. 二叉搜索树中的搜索

题目描述

难度：简单

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。

示例 1:
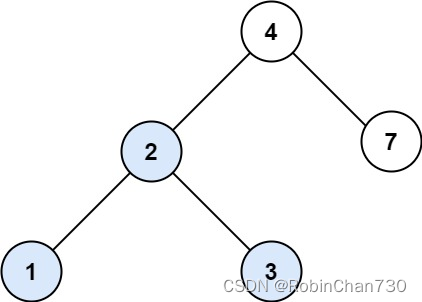
在这里插入图片描述

输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:
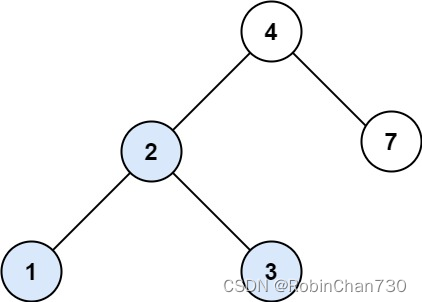
在这里插入图片描述

输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

树中节点数在 [1, 5000] 范围内
1 <= Node.val <= 10^7
root 是二叉搜索树
1 <= val <= 10^7

题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
#define SOLUTION 3
public:
#if SOLUTION == 1
    // 没有利用 二叉搜索树 的特征
    TreeNode* searchBST(TreeNode* root, int val) {
        // 终止条件
        if (root == nullptr) return nullptr;
        // 中
        if (root->val == val)   return root;
        // 左
        TreeNode* left = searchBST(root->left, val);
        if (left != nullptr && left->val  == val)   return left; 
        // 右
        TreeNode* right = searchBST(root->right, val);
        if (right != nullptr && right->val == val)  return right;
        return nullptr;        
    }
#elif SOLUTION == 2
    // 利用 二叉搜索树 的特征
    /*
    二叉搜索树是一个有序树
    若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
    若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
    它的左、右子树也分别为二叉排序树
    */
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == nullptr)    return nullptr;
        if (root->val == val)   return root;
        // 如果值比root->val大, 说明只有可能在右子树有
        else if (root->val < val) {
            // 只递归右子树
            TreeNode* right = searchBST(root->right, val);
            // 无论right是否为null, 都返回right
            return right;
        } else {
            // 否则，递归左子树
            TreeNode* left = searchBST(root->left, val);
            return left;
        }
    }
#elif SOLUTION == 3
    // 迭代法
    TreeNode* searchBST(TreeNode* root, int val) {
        // 模拟
        while (root != nullptr) {
            if (root->val == val)   return root;
            else if (root->val > val)   root = root->left; // 如果值大了,则往左边搜索
            else    root = root->right;  // 否则往右边
        }
        return root;
        
    }
#endif
};