所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

二、解法

  思路分析：本题难点在于要考虑到不同序列的情况，具体来说要考虑一下几种特殊情况：

• 1、上下坡中有平坡：[1 2 2 2 1];
• 2、数组首尾两端：[1 2] [1 1 2]；
• 3、单调坡中有平坡： [1 2 2 2 3 4 5]；
    观察一下不难发现，序列的最大摆动子序列的长度和局部峰值有关系。因此我们首先要找的就是局部峰值。定义preDiff和curDiff分别记录上一个差值和当前差值。对于小于等于1的序列直接输出其长度。贪心算法要做的就是删除单调区间内的元素。事实上也不需要去修改原序列，只需删除单一坡度上的节点，然后统计长度考虑局部峰值即可。情况一种仅有最大摆动子序列长度为3，我们统一删除前两个2 变成[1 2 1]长度为3。
  
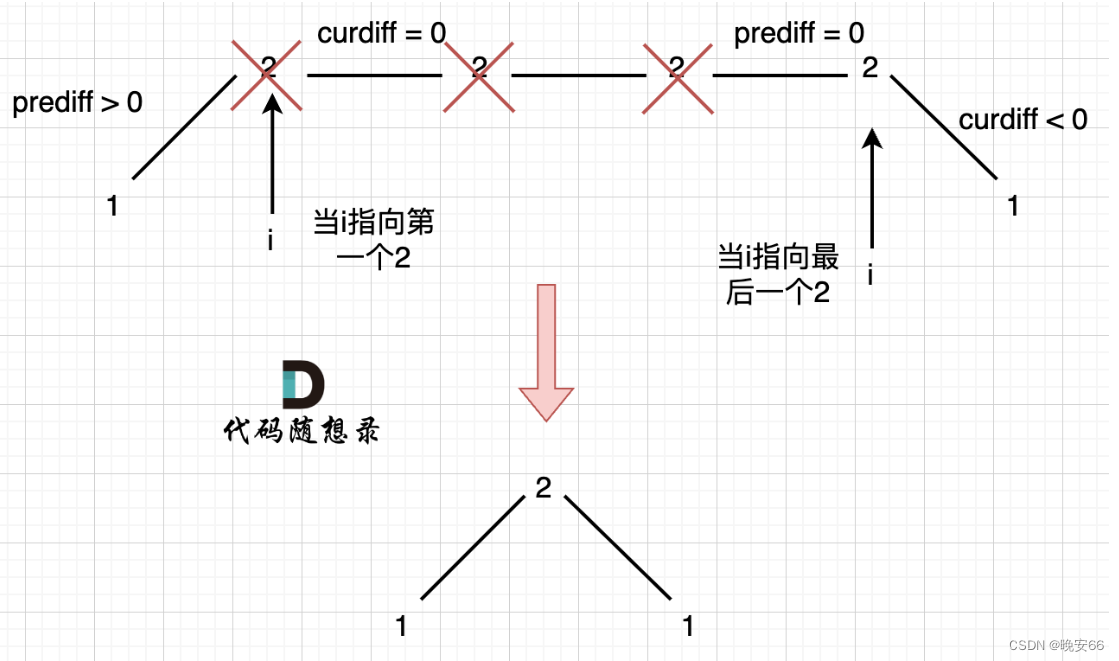
    对于情况2，我们假设默认最右边有一个峰值result=1，同时preDiff初始化为0，也就是说，[1 2]的序列可以看成[1 1 2]。这两个序列的最大摆动子序列长度相同，为2。
    对于情况3，我们选择在摆动变化的时候更新preDiff，而非每次curDiff变换就修改preDiff，因此在每个单调区间内preDiff只会发生一次变化。
  
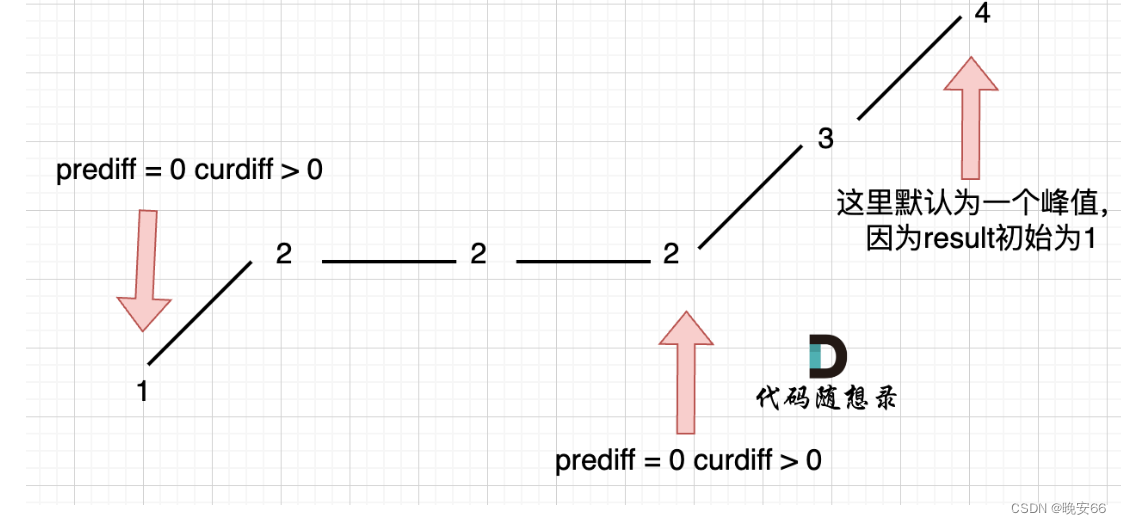
    程序如下：

class Solution {
public:
	int wiggleMaxLength(vector<int>& nums) {
		if (nums.size() <= 1) return nums.size();	// 序列元素小于等于1的情况
		int curDiff = 0;	// 记录当前差值
		int preDiff = 0;	// 记录上一个差值
		int result = 1;		// 记录峰值个数，默认序列最右边有一个峰值，序列的最大摆动子序列的长度和局部峰值有关
		for (int i = 0; i < nums.size() - 1; i++) {
			curDiff = nums[i + 1] - nums[i];
			if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {	// 出现局部峰值
				result++;
				preDiff = curDiff;	// 只在摆动变化的时候更新preDiff
			}	
		}
		return result;
	}
};

复杂度分析：

• 时间复杂度： $O(n)$。
• 空间复杂度：$O(1)$。

三、完整代码

# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;

class Solution {
public:
	int wiggleMaxLength(vector<int>& nums) {
		if (nums.size() <= 1) return nums.size();	// 序列元素小于等于1的情况
		int curDiff = 0;	// 记录当前差值
		int preDiff = 0;	// 记录上一个差值
		int result = 1;		// 记录峰值个数，默认序列最右边有一个峰值，序列的最大摆动子序列的长度和局部峰值有关
		for (int i = 0; i < nums.size() - 1; i++) {
			curDiff = nums[i + 1] - nums[i];
			if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {	// 出现局部峰值
				result++;
				preDiff = curDiff;	// 只在摆动变化的时候更新preDiff
			}	
		}
		return result;
	}
};

int main() {
	vector<int> nums = { 1, 17, 10, 13, 10, 16, 8 };
	Solution s1;
	int result = s1.wiggleMaxLength(nums);
	cout << result << endl;
	system("pause");
	return 0;
}

end